1 描述
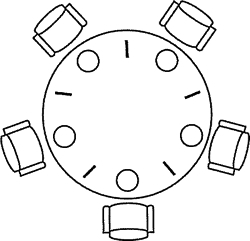
一张圆桌上坐着5名哲学家,每两个哲学家之间的桌上摆一根筷子,桌子的中间是一碗米饭,如图所示。哲学家们倾注毕生精力用于思考和进餐,哲学家在思考时,并不影响他人。只有当哲学家饥饿的时候,才试图拿起左、右两根筷子(一根一根地拿起)。如果筷子已在他人手上,则需等待。饥饿的哲学家只有同时拿到了两根筷子才可以开始进餐,当进餐完毕后,放下筷子继续思考。
2 分析
-
关系分析。 5名哲学家与左右邻居对其中间筷子的访问是互斥关系。
-
整理思路。 显然这里有五个进程。本题的关键是如何让一个哲学家拿到左右两个筷子而不造成死锁或者饥饿现象。那么解决方法有两个,一个是让他们同时拿两个筷子;二是对每个哲学家的动作制定规则,避免饥饿或者死锁现象的发生。
-
信号量设置。 定义互斥信号量数组Ch0PstiCk[5] = {l, 1, 1, 1, 1}用于对5个筷子的互斥访问。对哲学家按顺序从0~4编号,哲学家i左边的筷子的编号为i,哲学家右边的筷子的编号为(i+l)%5。
semaphore chopstick[5] = {1,1,1,1,1}; //定义信号量数组chopstick[5],并初始化
Pi(){ //i号哲学家的进程
while(1){
P(chopstick[i]); //取左边筷子
P(chopstick[(i+1)%5]); //取右边篌子
eat;
V(chopstick[i]); //放回左边筷子
V(chopstick[(i+1)%5]); //放回右边筷子
think;
}
}
该算法存在以下问题:当五个哲学家都想要进餐,分别拿起他们左边筷子的时候(都恰好执行完wait(chopstick[i]);)筷子已经被拿光了,等到他们再想拿右边的筷子的时候(执行 wait(chopstick[(i+l)%5]);)就全被阻塞了,这就出现了死锁。
为了防止死锁的发生,可以对哲学家进程施加一些限制条件,比如:
- 至多允许四个哲学家同时进餐;
- 仅当一个哲学家左右两边的筷子都可用时才允许他抓起筷子;
- 对哲学家顺序编号,要求奇数号哲学家先抓左边的筷子,然后再转他右边的筷子,而偶数号哲学家刚好相反。
3 解法
3.1 解法一
假设当一个哲学家左右两边的筷子都可用时,才允许他抓起筷子。
semaphore chopstick[5] = {1,1,1,1,1}; //初始化信号量
semaphore mutex=l; //设置取筷子的信号量
Pi(){ //i号哲学家的进程
while(1){
P(mutex); //在取筷子前获得互斥量,一次只能由一个哲学家取筷子
P(chopstick[i]) ; //取左边筷子
P(chopstick[(i+1)%5]); //取右边筷子
V(mutex); //释放取筷子的信号量
eat;
V(chopstick[i]); //放回左边筷子
V(chopstick[(i+1)%5]); //放回右边筷子
think;
}
}
3.2 解法二
至多只允许有四位哲学家同时去拿左边的筷子,最终能保证至少有一位哲学家能够进餐,并在用完时能释放出他用过的两只筷子,从而使更多的哲学家能够进餐。
semaphore chopstick[5] = {1,1,1,1,1}; //初始化信号量
semaphore eating = 4; //至多只允许四个哲学家可以同时进餐
Pi(){ //i号哲学家的进程
while(1){
think;
P(eating); //请求进餐,若是第五个则挨饿
P(chopstick[i]); //取左边筷子
P(chopstick[(i+1)%5]) ; //取右边筷子
eat;
V(chopstick[(i+1)%5]) ; //放回右边筷子
V(chopstick[i]) ; //放回左边筷子
V(eating); //释放信号量给其他挨饿的哲学家
}
}
3.3 解法三
仅当哲学家的左右两只筷子均可使用,才允许他拿起筷子进餐。
semaphore chopstick[5] = {1,1,1,1,1}; //初始化信号量
semaphore mutex = 1; //设置取筷子的信号量
Pi(){ //i号哲学家的进程
while(1){
think;
P(mutex); //在去筷子前获得互斥量
P(chopstick[i]); //取左边筷子
P(chopstick[(i+1)%5]) ; //取右边筷子
V(mutex); //释放互斥量
eat;
V(chopstick[(i+1)%5]) ; //放回右边筷子
V(chopstick[i]) ; //放回左边筷子
}
}
3.4 解法四
规定奇数号哲学家先拿他左边的筷子,然后在去拿右边的筷子;而偶数号哲学家则相反。按此规定,将是1、2号哲学家竞争1号筷子;3、4号哲学家竞争3号筷子。
即5位哲学家都先竞争奇数号筷子,获得后,再去竞争偶数号筷子,最后总会有一位哲学家能够获得两只筷子而进餐。
semaphore chopstick[5] = {1,1,1,1,1}; //初始化信号量
Pi(){ //i号哲学家的进程
while(1){
think;
if(i%2==0){
P(chopstick[(i+1)%5]) ; //取右边筷子
P(chopstick[i]); //取左边筷子
eat;
V(chopstick[(i+1)%5]) ; //放回右边筷子
V(chopstick[i]) ; //放回左边筷子
}else{ //奇数哲学家,先左后右
P(chopstick[i]); //取左边筷子
P(chopstick[(i+1)%5]) ; //取右边筷子
V(mutex); //释放互斥量
eat;
V(chopstick[i]) ; //放回左边筷子
V(chopstick[(i+1)%5]) ; //放回右边筷子
}
}
}
3.5 解法五
采用AND型信号量机制来解决,即要求每个哲学家先获得两个临界资源(筷子)后方能进餐。
semaphore chopstick[5] = {1,1,1,1,1}; //初始化信号量
semaphore mutex = 1; //设置取筷子的信号量
Pi(){
while(1){
think;
P(chopstick[i],chopstick[(i+1)%5]);
eat;
V(chopstick[i],chopstick[(i+1)%5]);
}
}
4 拓展
5个哲学家问题本质上是解决并发程序中的死锁和饥饿,可以将推广为更一般的n个进程,m个共享资源的问题。