A.Planting Trees
排序+模拟
常识问题,将耗时排一个序,时间长的先种,每次判断更新最后一天的时间。
代码:

#include <iostream> #include <cstdio> #include <cstring> #include <cmath> #include <algorithm> #define Mod 1000000007 #define INT 2147483647 #define pi acos(-1.0) #define eps 1e-3 #define lll __int64 #define ll long long using namespace std; #define N 100007 ll a[N]; int main() { int i,j,n; ll now,t; scanf("%d",&n); for(i=0;i<n;i++) scanf("%lld",&a[i]); t = 1; now = 0; sort(a,a+n); for(i=n-1;i>=0;i--) { now = max(now,t+a[i]); t++; } printf("%lld ",now+1); return 0; }
B.Boiling Vegetables
暴力
尽可能把每份切成相等的块,这样可以使差距最小化。
枚举最大块在哪种蔬菜中产生,然后枚举切的次数,将这种蔬菜切tim次得到tim+1份,即最大块为w[i]/(tim+1),算出此时至少的基准最小块的大小,然后枚举其他蔬菜来切,也要切成最接近最大块的大小,然后判断:1.总切刀数是否大于最优Best,2.切出来的块是否小于STDMin(基准最小块大小),如果两者有一个为非,退出此次枚举,返回上层。
代码:

#include <iostream> #include <cstdio> #include <cstring> #include <cmath> #include <algorithm> using namespace std; #define N 1027 double w[N]; int main() { int i,j,n,tim,Best,flag; double rati; scanf("%lf%d",&rati,&n); for(i=1;i<=n;i++) scanf("%lf",&w[i]); Best = 501; for(i=1;i<=n;i++) //枚举要切成最大块的那一种蔬菜 { for(tim=0;tim<Best;tim++) //枚举这种蔬菜被切的次数,不多于Best次 { double Bigest = w[i]/(tim+1); //最大块 double STDMin = Bigest*rati; //基准最小块 int Tcuts = tim; flag = 1; for(j=1;j<=n && flag;j++) //切其他的 { if(j == i) continue; int Cuts = (int)ceil(w[j]/Bigest) - 1; ////达到最大块以下需要切的刀数 if(w[j]/(Cuts+1) < STDMin) //切Cuts刀,分成Cuts+1份后如果每份小于基准最小块 flag = 0; Tcuts += Cuts; if(Tcuts >= Best) flag = 0; } if(flag && Tcuts < Best) Best = Tcuts; } } printf("%d ",Best); return 0; }
C.Number Trick
首先x>=10.0肯定没戏,因为首先位数就不等了。
设此数为A,有n位数,第一位为A0,则有A*X = (A - 10^(n-1))*10 + A0 (1),
进而得出:
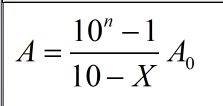 (2)
(2)
枚举位数n和第一位A0,得出A,再验证A是否合法:1.A/10^(n-1) = A0 (第一位是A0)2.是否满足(1)式
如果满足,输出。这题精度问题很烦。
代码:

#include <iostream> #include <cstdio> #include <cstring> #include <cmath> #include <algorithm> #define eps 1e-5 #define ll long long using namespace std; #define N 2027 int main() { int i,n; double x; cin>>x; if(x >= 10.0) { puts("No solution"); return 0; } int A0; int flag = 0; ll P = 1; for(n=1;n<=8;n++) { for(A0=1;A0<=9;A0++) { ll A = (10*P-1)*A0/(10-x) + 0.5; if(A/P == A0 && fabs((A-A0*P)*10+A0-A*x) < eps) { printf("%lld ",A); flag = 1; } } P *= 10; } if(!flag) puts("No solution"); return 0; }
D.Robert Hood
枚举
不要被100000一点吓到了,要对题目中的数字敏感,看到坐标值在(-1000~1000)之间,并且全是整数点的时候,想到有没有平方级的复杂度。
将二维化成一维,我这里化为y轴,其实x轴y轴都是一样的,对每个y轴的坐标值,维护纵坐标为y的一条线上x坐标值最小和x坐标最大的两个值,然后在y轴上以N^2的复杂度枚举(N:最大1000)每对y=Y的线(Y为固定值),设为线A和线B,纵坐标为YA和YB,每次求A的(XAmin,YA)到B的(XBmax,YB)的距离和A的(XAmax,YA)到B的(XBmin,YB)的距离,取一个最大值,循环完后得到结果。
因为坐标值有负,所以统一加上1000。
小技巧:dis函数可以不写sqrt,到最后求出最远距离再做一次sqrt即可,可节省时间。
代码:

#include <iostream> #include <cstdio> #include <cstring> #include <cmath> #include <algorithm> #define Mod 1000000007 #define INT 2147483647 #define lll __int64 #define ll long long using namespace std; #define N 2027 int vis[N],minx[N],maxx[N]; double dis(int x1,int y1,int x2,int y2) { return (double)sqrt((x1-x2)*(x1-x2) + (y1-y2)*(y1-y2)); } int main() { int n,i,j,x,y; memset(vis,0,sizeof(vis)); scanf("%d",&n); while(n--) { scanf("%d%d",&x,&y); y += 1000; if(!vis[y]) { minx[y] = maxx[y] = x; vis[y] = 1; } else { if(minx[y] > x) minx[y] = x; if(maxx[y] < x) maxx[y] = x; } } double res = -Mod; for(i=0;i<=2002;i++) { if(vis[i]) { for(j=i;j<=2002;j++) { if(!vis[j]) continue; double dis1 = dis(minx[i],i,maxx[j],j); double dis2 = dis(maxx[i],i,minx[j],j); res = max(res,max(dis1,dis2)); } } } printf("%.9lf ",res); return 0; }
E.Virus Replication
题目比较不好懂。意思是将第一个串的某些连续部分替换为某个子串使整个子串变成第二个串,求这个字串的最小长度(有可能为0)。
做法:从前往后匹配和从后往前匹配,设第一种的失配位置为low,第二种的适配位置为high(low,high的索引皆为其在第二个串的索引),则最小长度为max(0,high-low+1),但是还可能第二个串比第一个串长,这是想替换至少长度为len2-len1,所以考虑res = max(res,len2-len1)。
代码:

#include <iostream> #include <cstdio> #include <cstring> #include <cmath> #include <algorithm> #include <string> #define Mod 1000000007 #define INT 2147483647 using namespace std; #define N 1027 int main() { string a,b; while(cin>>a>>b) { int i,j; int len1 = a.length(); int len2 = b.length(); int low = 0; int high = len2-1; for(i=0;i<len1&&i<len2;i++) { if(a[i] != b[i]) break; low++; } j = len1-1; for(i=len2-1;i>=0&&j>=0;i--,j--) { if(a[j] != b[i]) break; high--; } int res = max(0,high-low+1); res = max(res,len2-len1); printf("%d ",res); } return 0; }
F.Timebumb
模拟题。比较水。
一个一个处理数字,将数字的15个点编号0~15,如果某点为‘*’,则编号1,否则编号0,。如果发现某个数字处不是数字的正确形式,则直接爆炸。否则统计看是否能模6为0.
代码:

#include <iostream> #include <cstdio> #include <cstring> #include <cmath> #include <algorithm> #include <cstdlib> #include <string> using namespace std; #define N 100007 char ss[7][33]; int vis[10][17]; string val[10] = {"111101101101111","001001001001001","111001111100111","111001111001111","101101111001001","111100111001111","111100111101111","111001001001001","111101111101111","111101111001111"}; string vis_to_01(int VIS[17]) { int i; string res = ""; for(i=0;i<15;i++) { if(VIS[i] == 1) res += '1'; else res += '0'; } return res; } int main() { int i,j,k; int len; for(i=0;i<5;i++) { gets(ss[i]); } len = strlen(ss[0]); int ind,lefti; char dig[10]; for(lefti=0,ind=0;lefti<=len-3;lefti+=4,ind++) { int k = 0; for(i=0;i<5;i++) { for(j=lefti;j<lefti+3;j++) { if(ss[i][j] == '*') { vis[ind][k] = 1; } else vis[ind][k] = 0; k++; } } } int flag = 1; for(i=0;i<ind;i++) { string now = vis_to_01(vis[i]); for(j=0;j<10;j++) { if(val[j] == now) { dig[i] = j + 48; break; } } if(j == 10) { flag = 0; break; } } int ka = atoi(dig); if(!flag || ka%6 != 0) puts("BOOM!!"); else puts("BEER!!"); return 0; }
G.Erase Securely
水。

#include <iostream> #include <cstdio> #include <cstring> #include <cmath> #include <algorithm> #include <cstdlib> #include <string> using namespace std; #define N 100007 int main() { int n,i,len; string a,b; int flag; scanf("%d",&n); cin>>a>>b; if(n%2) flag = 1; else flag = 0; len = a.length(); for(i=0;i<len;i++) { if(flag) { if(a[i] == b[i]) { break; } } else { if(a[i] != b[i]) break; } } if(i == len) puts("Deletion succeeded"); else puts("Deletion failed"); return 0; }
H.Pinball
I.Dance Reconstruction
J.Dartboard
微积分题。
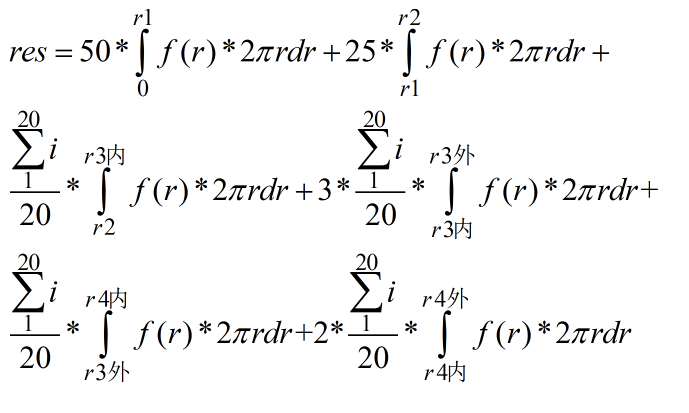
代码:

#include <iostream> #include <cstdio> #include <cstring> #include <cmath> #include <algorithm> #define eps 1e-3 using namespace std; #define N 100007 double theta; double calc(double r1,double r2) { return exp(-(r1*r1)/(2*theta*theta)) - exp(-(r2*r2)/(2*theta*theta)); } int main() { double r1,r2,r3,r4,r5,r6; scanf("%lf%lf%lf%lf%lf%lf",&r1,&r2,&r3,&r4,&r5,&r6); scanf("%lf",&theta); double res = 50.0*calc(0,r1) + 25.0*calc(r1,r2) + 10.5*calc(r2,r3) + 31.5*calc(r3,r4) + 10.5*calc(r4,r5) + 21.0*calc(r5,r6); printf("%lf ",res); return 0; }
K.Cliff Work
(没做出来的以后持续更新)
