提要
通过对上一篇A*寻路算法的学习,我们对A*寻路应该有一定的了解了。但实际应用中,须要对算法进行一些改进和优化。 Iterative Deepening Depth-first search- 迭代深化深度优先搜索
在深度优先搜索中一个比較坑爹情形就是在搜索树的一枝上没有要搜的结果,可是却非常深,甚至深不见底,这样就根本搜索不到结果。为了防止这样的情况出现,就出现了Iterative Deepening的思想。
迭代深化搜索(Iterative deepening search, IDS)或者(迭代深化深度优先搜索,Iterative deepening depth-first search)是一种经常使用的搜索机制,经常使用在深度优先搜索中.通过逐渐地提高深度限制搜索(Depth-limited search)的深度限制(depth limit)——从1開始,然后2,一直到找到目标结点位置为止——迭代深化搜索可以找出最好的深度限制.深度限制搜索指的是在深度优先搜索中,引入深度限制limit,假设从根结点出发到结点N的深度为limit,那么N被当做没有子结点的叶结点那样处理.
找一棵树来详细看一下。
须要找ee节点。
首先把深度限制设置为1。则要搜索的树为
对其进行深度优先搜索。没搜到。添加深度限制为2.
进行DFS还是没搜索到,继续添加深度限制到3.
进行DFS,Bingo,找到。
和直接用DFS一样啊。看起来傻傻的? No!
这种方法首先规避了最開始说的DFS深度的问题,相对于BFS一般须要存储产生的所有结点,占的存储空间要比深度优先大得多。ID-DFS它的内存占用又少非常多。再来看看时间复杂度.
迭代深化搜索或许看起来比較浪费时间,由于状态有可能被多次产生.可是事实并不是如此,由于大多数的结点处在底层,而底层结点的搜索次数非常少.对于一个深度为d,分支因子为b的树,.最多须要搜索的结点个数为: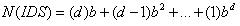
故此迭代深化搜索的时间复杂度和深度优先搜索的一样是O( bk)
So... 这个算法是两种搜索方法的折中,BFS能搜索到的,它就一定能搜到。并且不用那么多的空间,仅仅需牺牲一点点的时间(相同的节点可能要訪问非常多次)。
以下是一个一般一些的样例,包括了三种算法的对照。
Iterative Deepening A*
迭代延伸A*可以简写成IDA*,用的也是迭代延伸的思想,这里的bounding就不再是树的深度了。而是 f(n) 的值。
首先还是从s出发,,bounding的值就是f(s),接下来就是从s进行深度优先搜索,f() 值大约阈值的所有无论。没有找到的话就增大阈值,再进行DFS....直到最后找到终于的节点。
非常明显,IDA*用深度优先搜索替代了Open List 和Close List, 降低了内存上的开销,也少了List维护的花费。尽管每次搜索都要从头開始,这看上去一次重新去搜索相同的节点有点不合理,可是这个代价远远低于原版本号中维护Open List和Close List.
边缘搜索A*
A*算法最大的性能问题就是Open List和Close List的维护,IDA*最大的问题就是无法记忆维护历史。会反复搜寻节点。一个新的寻路算法 - 边缘搜索A*。A*和IDA*的折中。
它维护了两个List。Now和Later来记录搜索的边缘点,同一时候用IDA*的思想来推进。详细看一下伪代码。
now - linked list of search nodes, list order determines order of evaluation later - linked list of search nodes root - start node threshold = root's g() push root into now while now not empty for each node in now if node == goal stop if node's f() > threshold push node onto end of later else insert children of node into now behind node remove node from now and discard push later onto now, clear later set threshold = minimum g() found that is higher than current threshold
now中存放的是当先须要被评估的节点,later中存放的是下一次将要评估的节点。
这个过程以比較弱的排序来维护列表,并且以像IDA*的深度优先的方式来有效地扩展节点。假设一次完毕遍历now之后没有找到目标,则添加threshold值。later列表变成now列表,搜索又从now列表的顶点開始。尽管搜索过程须要now和later列表的维护,却没有排序的开销,并且内存的消耗比A*少太多。
參考
Artificial Intelligence 3.7 - http://www.cs.ubc.ca/~poole/aibook/html/ArtInt_62.html
Iterative Deepening - http://www.comp.lancs.ac.uk/computing/research/aai-aied/people/paulb/old243prolog/subsection3_6_4.html
Game Programming Gems 3.7




