POJ 题目2750 Potted Flower（线段树求环型区间中连续区间的最大和）

Potted Flower

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions: 4470		Accepted: 1698

Description

The little cat takes over the management of a new park. There is a large circular statue in the center of the park, surrounded by N pots of flowers. Each potted flower will be assigned to an integer number (possibly negative) denoting how attractive it is. See the following graph as an example: 

(Positions of potted flowers are assigned to index numbers in the range of 1 ... N. The i-th pot and the (i + 1)-th pot are consecutive for any given i (1 <= i < N), and 1st pot is next to N-th pot in addition.) 



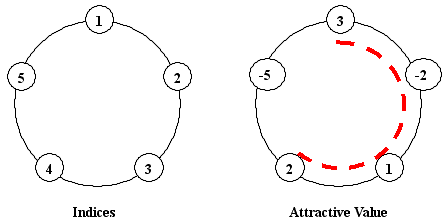
The board chairman informed the little cat to construct "ONE arc-style cane-chair" for tourists having a rest, and the sum of attractive values of the flowers beside the cane-chair should be as large as possible. You should notice that a cane-chair cannot be a total circle, so the number of flowers beside the cane-chair may be 1, 2, ..., N - 1, but cannot be N. In the above example, if we construct a cane-chair in the position of that red-dashed-arc, we will have the sum of 3+(-2)+1+2=4, which is the largest among all possible constructions. 

Unluckily, some booted cats always make trouble for the little cat, by changing some potted flowers to others. The intelligence agency of little cat has caught up all the M instruments of booted cats' action. Each instrument is in the form of "A B", which means changing the A-th potted flowered with a new one whose attractive value equals to B. You have to report the new "maximal sum" after each instruction. 

Input

There will be a single test data in the input. You are given an integer N (4 <= N <= 100000) in the first input line. 

The second line contains N integers, which are the initial attractive value of each potted flower. The i-th number is for the potted flower on the i-th position. 

A single integer M (4 <= M <= 100000) in the third input line, and the following M lines each contains an instruction "A B" in the form described above. 

Restriction: All the attractive values are within [-1000, 1000]. We guarantee the maximal sum will be always a positive integer. 

Output

For each instruction, output a single line with the maximum sum of attractive values for the optimum cane-chair.

Sample Input

5
3 -2 1 2 -5
4
2 -2
5 -5
2 -4
5 -1

Sample Output

4
4
3
5

Source

POJ Monthly--2006.01.22,Zeyuan Zhu

题目大意：求环形的区间中连续区间的最大和。，可是不能都取

maxv连续区间最大和

minv连续区间的最小和

lmax从左最大

lmin从左最小

rmax从右最大

rmin从有最小

sum区间全部数的和

ac代码

#include<stdio.h>
#include<string.h>
#define max(a,b) (a>b?a:b)
#define min(a,b) (a>b?
b:a)
struct s
{
	int sum;
	int maxv,minv;
	int lmin,lmax;
	int rmin,rmax;
}node[100010<<2];
void init(int tr,int num)
{
	node[tr].sum=num;
	node[tr].maxv=node[tr].minv=num;
	node[tr].lmin=node[tr].lmax=num;
	node[tr].rmin=node[tr].rmax=num;
}
void pushup(int tr)
{
	node[tr].sum=node[tr<<1].sum+node[tr<<1|1].sum;
	node[tr].lmax=max(node[tr<<1].lmax,node[tr<<1].sum+node[tr<<1|1].lmax);
	node[tr].rmax=max(node[tr<<1|1].rmax,node[tr<<1|1].sum+node[tr<<1].rmax);
	node[tr].lmin=min(node[tr<<1].lmin,node[tr<<1].sum+node[tr<<1|1].lmin);
	node[tr].rmin=min(node[tr<<1|1].rmin,node[tr<<1|1].sum+node[tr<<1].rmin);
	node[tr].maxv=max(max(node[tr<<1].maxv,node[tr<<1|1].maxv),node[tr<<1].rmax+node[tr<<1|1].lmax);
	node[tr].minv=min(min(node[tr<<1].minv,node[tr<<1|1].minv),node[tr<<1].rmin+node[tr<<1|1].lmin);
}
void build(int l,int r,int tr)
{
	if(l==r)
	{
		int num;
		scanf("%d",&num);
		init(tr,num);
		return;
	}
	int mid=(l+r)>>1;
	build(l,mid,tr<<1);
	build(mid+1,r,tr<<1|1);
	pushup(tr);
	//node[tr].sum=node[tr<<1].sum+node[tr<<1|1].sum;
}
void update(int pos,int num,int l,int r,int tr)
{
	if(l==r)
	{
		init(tr,num);
		return;
	}
	int mid=(l+r)>>1;
	if(pos<=mid)
		update(pos,num,l,mid,tr<<1);
	else
		update(pos,num,mid+1,r,tr<<1|1);
	pushup(tr);
}
int main()
{
	int n;
	while(scanf("%d",&n)!=EOF)
	{
		build(1,n,1);
		int m;
		scanf("%d",&m);
		while(m--)
		{
			int a,b;
			scanf("%d%d",&a,&b);
			update(a,b,1,n,1);
			if(node[1].sum==node[1].maxv)//不能都取
			{
				printf("%d
",node[1].sum-node[1].minv);
			}
			else
				printf("%d
",max(node[1].sum-node[1].minv,node[1].maxv));//环
		}
	}
}