Description
给一个N个点M条边的连通无向图,满足每条边最多属于一个环,有Q组询问,每次询问两点之间的最短路径。
Input
输入的第一行包含三个整数,分别表示N和M和Q 下接M行,每行三个整数v,u,w表示一条无向边v-u,长度为w 最后Q行,每行两个整数v,u表示一组询问
Output
输出Q行,每行一个整数表示询问的答案
Sample Input
9 10 2
1 2 1
1 4 1
3 4 1
2 3 1
3 7 1
7 8 2
7 9 2
1 5 3
1 6 4
5 6 1
1 9
5 7
1 2 1
1 4 1
3 4 1
2 3 1
3 7 1
7 8 2
7 9 2
1 5 3
1 6 4
5 6 1
1 9
5 7
Sample Output
5
6
6
HINT
对于100%的数据,N<=10000,Q<=10000
正解:仙人掌+圆方树。
这道题直接判环好像很不好写的样子。。于是我去学了圆方树。
圆方树其实就是边双连通分量缩点。。把一个环上的点全部连到一个新点上,把这个点称作方点,其他点都是圆点。
不是环上的边就直接按照原图连就行了。
然后我们可以发现,这样得到的树和原来的仙人掌其实是等价的。
参见神犇博客:http://www.cnblogs.com/zzqsblog/p/5851393.html
蒯两个图:
仙人掌:
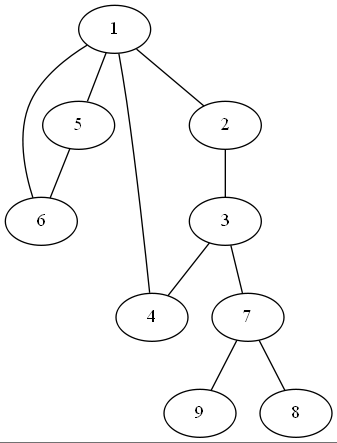
圆方树:
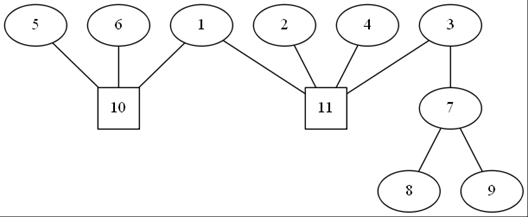
如何给这棵树设边权?如果是两个圆点之间的边,那么边权就是原边权,如果是圆方点之间的边,那么边权就是圆点到那个环顶的最短路径。
如何查询两点间最短路径?首先我们发现,如果两点的$LCA$是圆点,那么最短路就是两点之间距离,否则就要特判一下$LCA$的那两个儿子在环上的最短距离。
于是我们就能成功地解决仙人掌最短路问题了。
150行。。写得我要爽死了。。
1 //It is made by wfj_2048~ 2 #include <algorithm> 3 #include <iostream> 4 #include <complex> 5 #include <cstring> 6 #include <cstdlib> 7 #include <cstdio> 8 #include <vector> 9 #include <cmath> 10 #include <queue> 11 #include <stack> 12 #include <map> 13 #include <set> 14 #define inf (1<<30) 15 #define N (40010) 16 #define il inline 17 #define RG register 18 #define ll long long 19 #define File(s) freopen(s".in","r",stdin),freopen(s".out","w",stdout) 20 21 using namespace std; 22 23 int n,m,q; 24 25 struct edge{ int nt,to,dis; }; 26 27 struct YFtree{ 28 29 edge g[2*N]; int head[N],top[N],fa[N],son[N],dep[N],tid[N],pos[N],sz[N],dis[N],D[N],fg[N],nn,num,cnt; 30 31 il void insert(RG int from,RG int to,RG int dis){ 32 g[++num]=(edge){head[from],to,dis},head[from]=num; swap(from,to); 33 g[++num]=(edge){head[from],to,dis},head[from]=num; return; 34 } 35 36 il void dfs1(RG int x,RG int p){ 37 fa[x]=p,dep[x]=dep[p]+1,sz[x]=1; RG int v; 38 for (RG int i=head[x];i;i=g[i].nt){ 39 v=g[i].to; if (v==p) continue; 40 dis[v]=dis[x]+g[i].dis; 41 dfs1(v,x),sz[x]+=sz[v]; 42 if (sz[son[x]]<=sz[v]) son[x]=v; 43 } 44 return; 45 } 46 47 il void dfs2(RG int x,RG int p,RG int anc){ 48 top[x]=anc,tid[x]=++cnt,pos[cnt]=x; 49 if (son[x]) dfs2(son[x],x,anc); RG int v; 50 for (RG int i=head[x];i;i=g[i].nt){ 51 v=g[i].to; if (v==p || v==son[x]) continue; 52 dfs2(v,x,v); 53 } 54 return; 55 } 56 57 il int lca(RG int u,RG int v){ 58 while (top[u]!=top[v]){ 59 if (dep[top[u]]<dep[top[v]]) swap(u,v); 60 u=fa[top[u]]; 61 } 62 return dep[u]<dep[v] ? u : v; 63 } 64 65 il int jump(RG int u,RG int Lca){ 66 RG int last; 67 while (top[u]!=top[Lca]) 68 last=top[u],u=fa[top[u]]; 69 return u==Lca ? last : pos[tid[Lca]+1]; 70 } 71 72 il int query(RG int u,RG int v){ 73 RG int Lca=lca(u,v); 74 if (Lca<=n) return dis[u]+dis[v]-2*dis[Lca]; 75 RG int uu=jump(u,Lca),vv=jump(v,Lca); 76 RG int du=dis[uu]-dis[Lca],dv=dis[vv]-dis[Lca]; 77 if (!fg[uu]) du=D[Lca]-du; if (!fg[vv]) dv=D[Lca]-dv; 78 if (du>dv) swap(du,dv); 79 return dis[u]-dis[uu]+dis[v]-dis[vv]+min(dv-du,D[Lca]-(dv-du)); 80 } 81 82 }YF; 83 84 struct Graph{ 85 86 edge g[2*N]; int head[N],fa[N],dep[N],dis[N],dfn[N],low[N],st[N],num,cnt; 87 88 il void insert(RG int from,RG int to,RG int dis){ 89 g[++num]=(edge){head[from],to,dis},head[from]=num; return; 90 } 91 92 il void dfs(RG int x,RG int p){ 93 fa[x]=p,dep[x]=dep[p]+1,dfn[x]=low[x]=++cnt; RG int v; 94 for (RG int i=head[x];i;i=g[i].nt){ 95 v=g[i].to; if (v==p) continue; 96 if (!dfn[v]){ 97 dis[v]=dis[x]+g[i].dis,dfs(v,x); 98 low[x]=min(low[x],low[v]); 99 } else low[x]=min(low[x],dfn[v]); 100 if (dfn[x]<low[v]) YF.insert(x,v,g[i].dis); 101 } 102 for (RG int i=head[x];i;i=g[i].nt){ 103 v=g[i].to; if (v==p) continue; 104 if (fa[v]!=x && dfn[x]<dfn[v]) build(x,v,g[i].dis); 105 } 106 return; 107 } 108 109 il void build(RG int rt,RG int x,RG int d){ 110 RG int top=dep[x]-dep[rt]+1,tot=d,Dis=0; 111 for (RG int i=x;i!=rt;i=fa[i]) 112 st[top--]=i,tot+=dis[i]-dis[fa[i]]; 113 YF.D[++YF.nn]=tot,st[1]=rt,top=dep[x]-dep[rt]+1; 114 for (RG int i=1;i<=top;++i){ 115 RG int dd=min(Dis,tot-Dis); 116 YF.fg[st[i]]=dd==Dis; 117 YF.insert(YF.nn,st[i],dd); 118 Dis+=dis[st[i+1]]-dis[st[i]]; 119 } 120 return; 121 } 122 123 }G; 124 125 il int gi(){ 126 RG int x=0,q=1; RG char ch=getchar(); 127 while ((ch<'0' || ch>'9') && ch!='-') ch=getchar(); 128 if (ch=='-') q=-1,ch=getchar(); 129 while (ch>='0' && ch<='9') x=x*10+ch-48,ch=getchar(); return q*x; 130 } 131 132 il void work(){ 133 n=gi(),m=gi(),q=gi(); YF.nn=n; 134 for (RG int i=1,u,v,w;i<=m;++i){ 135 u=gi(),v=gi(),w=gi(); 136 G.insert(u,v,w),G.insert(v,u,w); 137 } 138 G.dfs(1,0); YF.dfs1(1,0); YF.dfs2(1,0,1); 139 for (RG int i=1,u,v;i<=q;++i){ 140 u=gi(),v=gi(); 141 printf("%d ",YF.query(u,v)); 142 } 143 return; 144 } 145 146 int main(){ 147 File("shortest"); 148 work(); 149 return 0; 150 }