题目:
方伯伯在自己的农田边散步,他突然发现田里的一排玉米非常的不美。这排玉米一共有N株,它们的高度参差不齐。方伯伯认为单调不下降序列很美,所以他决定先把一些玉米拔高,再把破坏美感的玉米拔除掉,使得剩下的玉米的高度构成一个单调不下降序列。方伯伯可以选择一个区间,把这个区间的玉米全部拔高1单位高度,他可以进行最多K次这样的操作。拔玉米则可以随意选择一个集合的玉米拔掉。问能最多剩多少株玉米,来构成一排美丽的玉米
n<=10000 , k <= 500
我第一眼想差分,但是发现不可做,因为我不会在差分上跑最长不降子序列╮( ̄⊿ ̄")╭
仔细思考一会之后看了题解好像有个好性质:
对于最优解,拔高区间右界必须为n
其实很显然(那你为什么看题解),如果拔高时不带上右边的玉米,显然对右边的玉米能否加入序列不利,而拔高时带上右边的玉米是“免费的”,
发现这个性质后,这个DP突然变得很简单,我挑出来一个序列,序列中“降”的值不超过k,就像这样
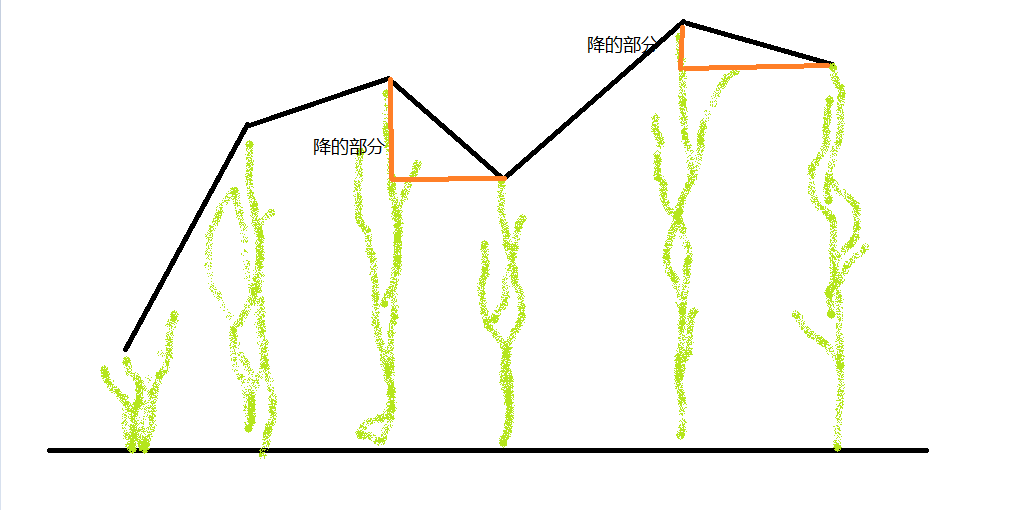
没错 这图是我画的 不然怎么能这么丑
突然很清晰了有没有?
这里我们可以自己可以口胡出来方程,dp[以第i个为结尾的序列][用了k次拔高] = 这个序列的长度
转移为dp[i][k] = max(dp[j][k-q]+1,dp[i][k])其中q为需要拔高多少(如果不用则为0),j为i前的玉米
欢欢喜喜写完过样例一交10pts,剩下全 泰拉E TLE,啥啊?
仔细一想O(10000 * 10000 * 500) = O(500,0000,0000)五百亿.....
孩子只做过矩阵加速DP,但这题不能矩阵啊.....难过的又去看了题解,真就二维树状数组啊.....
赶紧去学习了一下这是个什么高级东西,好像也不太难,就是在二维上干跟一维一样的事,
可以看出我们要快速取出dp[j][k-q]中的最大值,考虑用二维树状数组取出最大值
我们尝试改变dp数组的含义
dp[第i个拔高后的高度j][拔了k次],这样相对爽,因为这样可以直接拽出来高度对应的答案
直接把dp改为二维树状数组,dp[至多到第i个拔高后的高度j][至多拔了k次],发现爆了空间
用01背包思想去掉第一维并在dp时倒序
1 #include<bits/stdc++.h> 2 3 using namespace std ; 4 5 int a[10010],n,m,upl; 6 int dp[5510][510]; 7 8 int lowbit(int x){ 9 return x&-x; 10 } 11 12 void add(int x,int y,int a){ 13 for(int i=x;i<=upl;i+=lowbit(i)){ 14 for(int j=y;j<=m+1;j+=lowbit(j)){ 15 dp[i][j] = max(dp[i][j],a); 16 } 17 } 18 } 19 20 int ask(int x,int y){ 21 int ret = 0; 22 for(int i=x;i>=1;i-=lowbit(i)){ 23 for(int j=y;j>=1;j-=lowbit(j)){ 24 ret = max(dp[i][j],ret); 25 } 26 } 27 return ret; 28 } 29 30 int main(){ 31 ios::sync_with_stdio(false); 32 cin>>n>>m; 33 for(int i=1;i<=n;i++){ 34 cin>>a[i]; 35 upl = max(upl,a[i]); 36 } 37 upl += m; 38 int ans = 0; 39 for(int i=1;i<=n;i++){ 40 for(int k=m;k>=0;k--){ 41 int x = ask(a[i]+k,k + 1) + 1; 42 ans = max(x,ans); 43 add(a[i]+k,k+1,x); 44 } 45 } 46 cout<<ans<<endl; 47 return 0; 48 }