1091. Shortest Path in Binary Matrix

In an N by N square grid, each cell is either empty (0) or blocked (1).

A clear path from top-left to bottom-right has length k if and only if it is composed of cells C_1, C_2, ..., C_k such that:

• Adjacent cells C_i and C_{i+1} are connected 8-directionally (ie., they are different and share an edge or corner)
• C_1 is at location (0, 0) (ie. has value grid[0][0])
• C_k is at location (N-1, N-1) (ie. has value grid[N-1][N-1])
• If C_i is located at (r, c), then grid[r][c] is empty (ie. grid[r][c] == 0).

Return the length of the shortest such clear path from top-left to bottom-right.  If such a path does not exist, return -1.

Example 1:

Input: [[0,1],[1,0]]


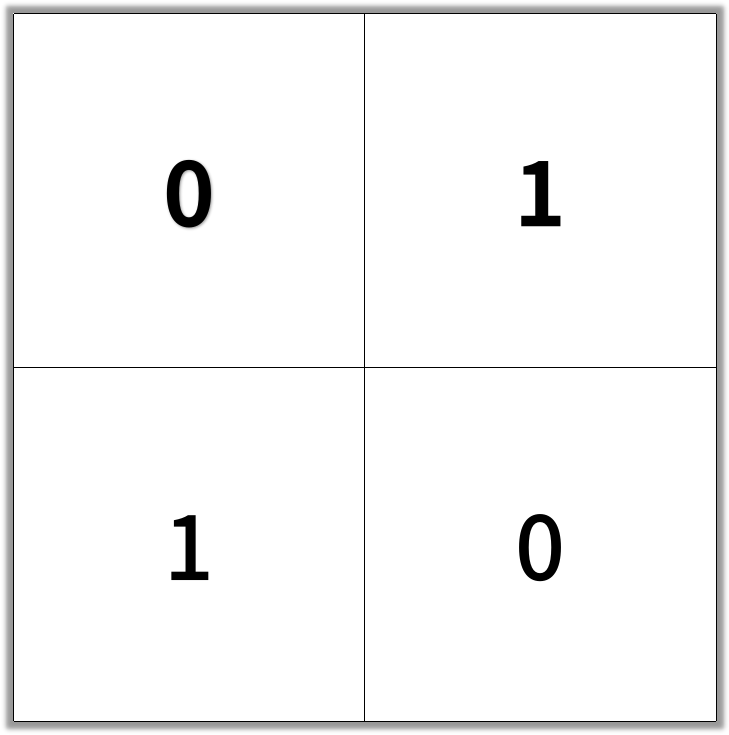Output: 2

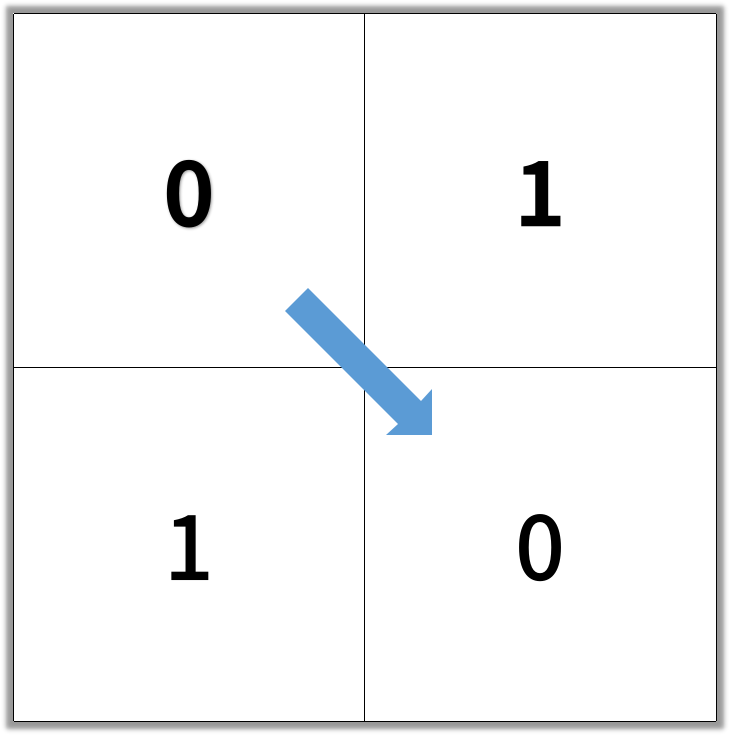
Example 2:

Input: [[0,0,0],[1,1,0],[1,1,0]]


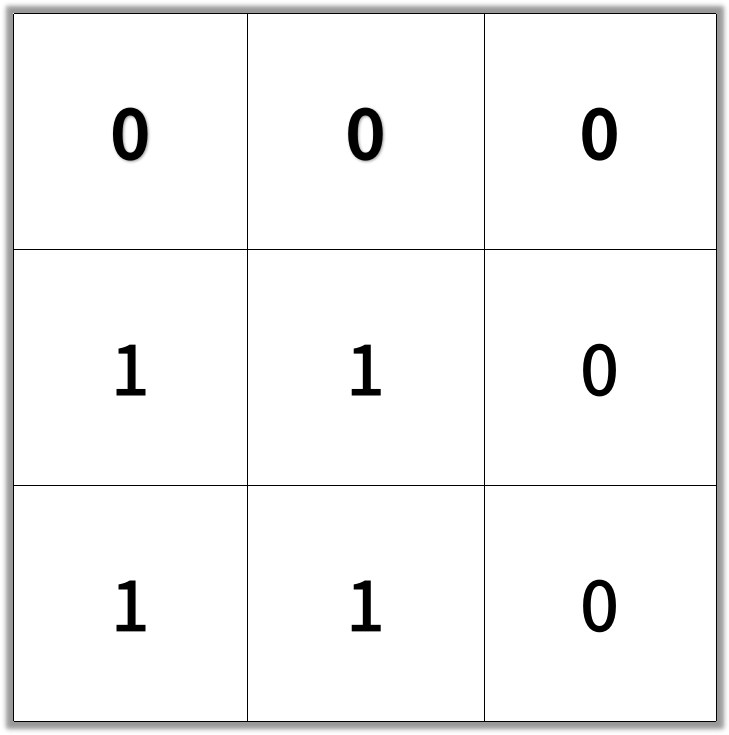Output: 4

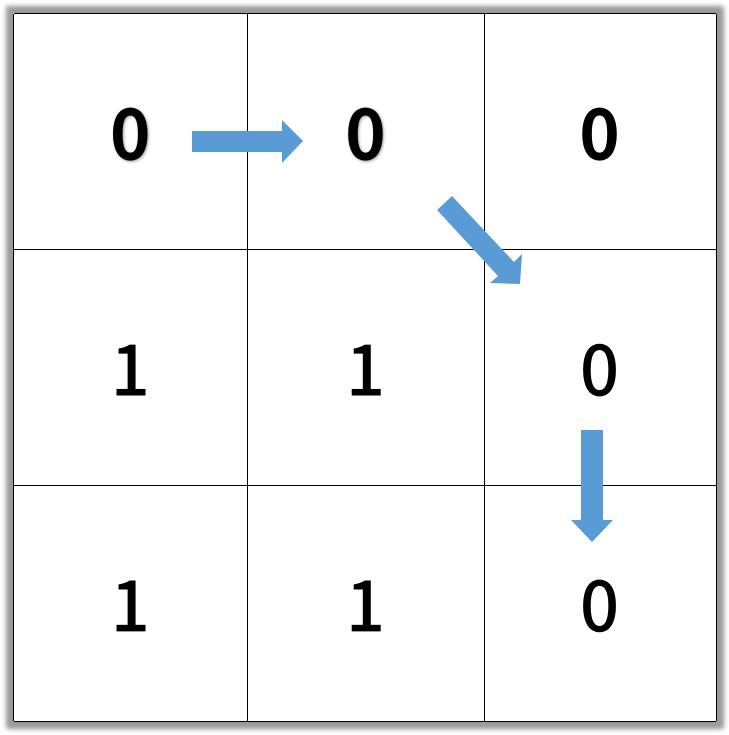
Note:

1. 1 <= grid.length == grid[0].length <= 100
2. grid[r][c] is 0 or 1

class Solution {
    private int dir[][] = new int[][]{{0,1},{0,-1},{1,0},{-1,0},{1,-1},{-1,1},{-1,-1},{1,1}};

        public int shortestPathBinaryMatrix(int[][] grid) {

            int m = grid.length;
            int n = grid[0].length;

            if(grid[0][0]==1 || grid[m-1][n-1]==1) {
                return -1;
            }

            boolean[][] visited = new boolean[m][n];
            visited[0][0] = true;
            Queue<int[]> queue = new LinkedList<>();
            queue.add(new int[]{0,0});

            int ans=0;
            while (!queue.isEmpty()) {
                int size = queue.size();
                for(int i=0;i<size;i++) {
                    int[] pop = queue.remove();
                    if(pop[0]==m-1 && pop[1]==n-1) {
                        return ans+1;
                    }
                    for (int k=0;k<8;k++) {
                        int nextX = dir[k][0]+pop[0];
                        int nextY = dir[k][1]+pop[1];

                        if(nextX>=0 && nextX<m && nextY>=0 && nextY<n && !visited[nextX][nextY] && grid[nextX][nextY]==0) {
                            queue.add(new int[]{nextX,nextY});
                            visited[nextX][nextY]=true;
                        }

                    }
                }
                ans++;
            }

            return -1;
        }
}

bfs处理无向图最短路径问题，dfs会TLE