存款利息的计算。有1000元,想存5年,可按以下5种办法存:
(1)一次存5年期
(2)先存2年期,到期后将本息再存3年期
(3)先存3年期,到期后将本息再存2年期
(4)存1年期,到期后将本息再存1年期,连续存5次
(5)存活期存款,活期利息每一季度结算一次
2017年银行存款利息如下:
1年期定期存款利息为1.5%;
2年期定期存款利息为2.1%;
3年期定期存款利息为2.75%;
5年期定期存款利息为3%;
活期存款利息为0.35%(活期存款每一-季度结算一-次利息)
如果r为年利率,n为存款年数,则计算本息的公式如下:
1年期本息和: P= 1000* (1+r);
n年期本息和: P= 1000* (1+n* r);
存n次1年期的本息和: $P=1000* (1+r)^n$;
活期存款本息和: P= 1000 *(1+$frac{r}{4}$)$^{4n}$;
说明: 1000*(1+$frac{r}{4}$)是一个季度的本息和。
题目解析:
理解题意很关键,其次就是利用数学库math中pow函数进行幂次方计算
代码示例:
#include<stdio.h>
#include <math.h>
int main()
{
float r5, r3, r2, r1, r0, p, p1, p2, p3, p4, p5;
p = 1000;
r5 = 0.0585;
r3 = 0.054;
r2 = 0.0468;
r1 = 0.0414;
r0 = 0.0072;
p1 = p*((1 + r5) * 5); // 一次存5年期
p2 = p*(1 + 2 * r2)*(1 + 3 * r3); // 先存2年期,到期后将本息再存3年期
p3 = p*(1 + 3 * r3)*(1 + 2 * r2); // 先存3年期,到期后将本息再存2年期
p4 = p*pow(1 + r1, 5); // 存1年期,到期后将本息存再存1年期,连续存5次
p5 = p*pow(1 + r0 / 4, 4 * 5); // 存活期存款。活期利息每一季度结算一次
printf("p1=%f
", p1); // 输出按第1方案得到的本息和
printf("p2=%f
", p2); // 输出按第2方案得到的本息和
printf("p3=%f
", p3); // 输出按第3方案得到的本息和
printf("p4=%f
", p4); // 输出按第4方案得到的本息和
printf("p5=%f
", p5); // 输出按第5方案得到的本息和
return 0;
}
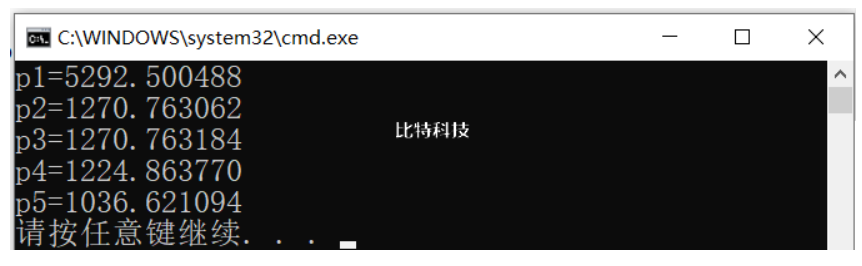
运行结果: