线代笔记
——https://space.bilibili.com/88461692#/
1.线性相关
(1)你有多个向量,并且可以移除其中一个而不减少张成的空间,当这种情况发生时,相关术语称它们是“线性相关”的。另一种表述就是,这个向量可以表示为其它向量的线性组合,因为这个向量已经落在其它向量张成的空间之中。
另一方面,如果所有向量都给张成的空间增添了新的维度,它们就是线性无关的。对于向量而言,两个向量线性无关可以简单的认为,只要两个向量中的各个数字不是成倍的就行。
2.线性变换
(1)如果一个变换具有如下两条性质,我们就称它是线性的,一是直线在变换后仍然保持为直线,不能有所弯曲,二是原点的位置必须保持固定。(猜测:这样才能保证可加性和成比例(数乘性))。应该把线性变换看作是“保持网格线平行且等距分布”的变换。
仿射变换,又称仿射映射,是指在几何中,一个向量空间进行一次线性变换并接上一个平移,变换为另一个向量空间。
(2)矩阵对某一向量进行变换,(a,c)和(b,d)各是进行线性变换过后的一组基向量,(a,c)是x轴,(b,d)是y轴。向量(x,y)则是标准坐标系的一个向量的坐标值,标准坐标系下,向量(x,y)是以(1,0),(0,1)作为基定义的,表达式:(x,y)=x*(1,0)+y*(0,1)。现在基变成了(a,c)和(b,d),由于是线性变换,关系不变,只是在原先的坐标系看来,你的坐标被拉伸了。所以x*(a,c)+y*(b,d)就是(x,y)经此矩阵变换过后的在标准坐标系中的向量坐标。
在变换后的坐标系中,还是按照(x,y)去描述,只不过是基向量不同。而它在标准坐标系中的坐标变成了(ax+by,cx+dy)。


(图:变换过程)
(3)矩阵本质就是变换,如果变换后的基向量是线性相关的。例如下图,以此作为基向量是展开不了空间的。由于两个基向量重合在一条线上,经历此变换的话,会将二维空间压缩到一条直线上,降至一维空间。
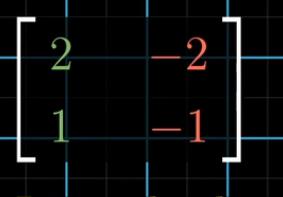
3.矩阵乘法
首先一个向量经历矩阵M1(旋转矩阵)变换,再经历矩阵M2(剪切矩阵)变换。结果而言最是一组新的基向量组成的线性空间。那么这组新的基向量组成的线性空间实际上相当于2次矩阵变换的乘积。
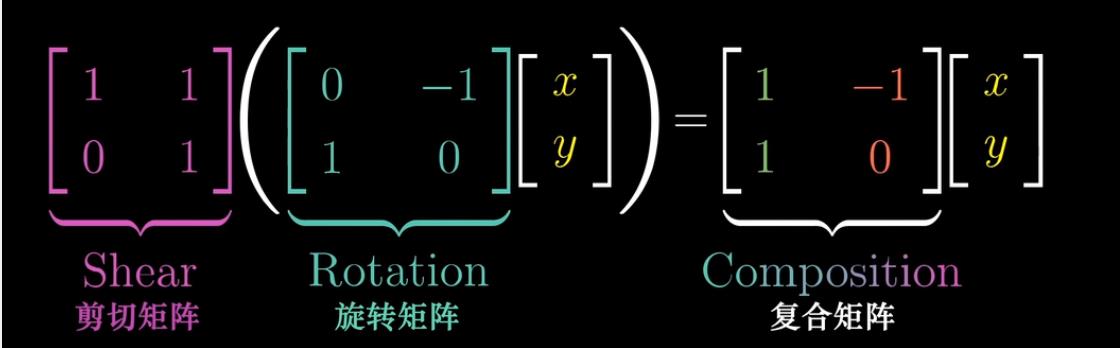
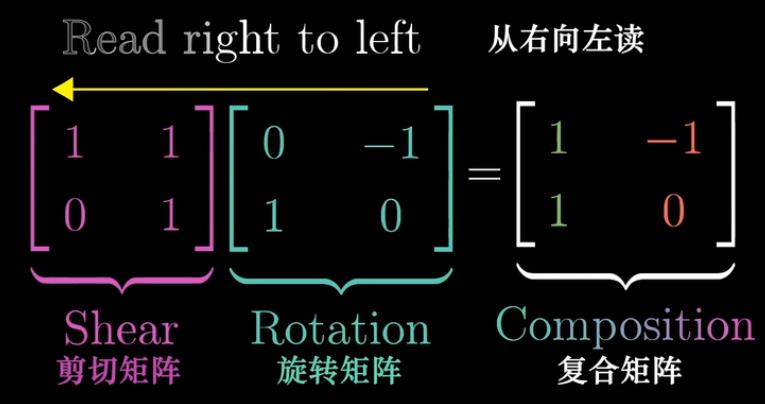
需要注意的是,理解的时候这里需要从右往左读,也就是书写表达式的时候,先应用的变换得写在右面,后应用的变换要写在左面。类似用f(g(x)的函数记号方法。
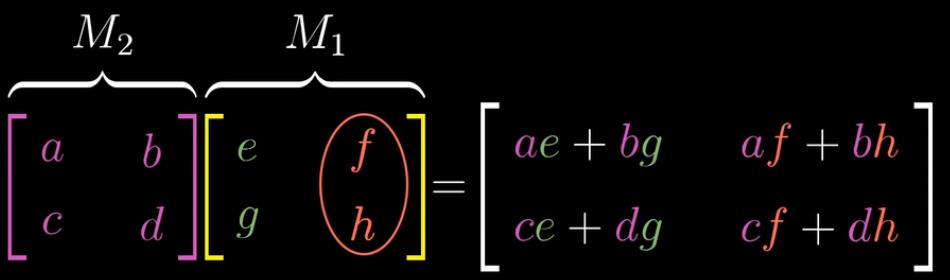
首先想象一下,M1的线性空间内的基向量i:(1,1)和j:(-2,0)要进行矩阵M2的线性变换。
那么先执行i向量的线性变换。
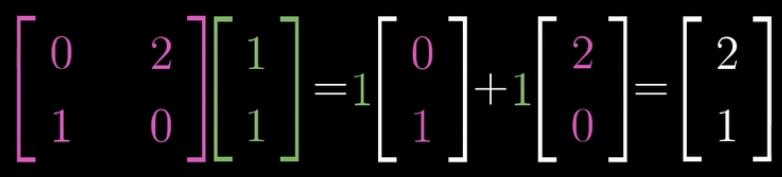
再执行j向量的线性变换。
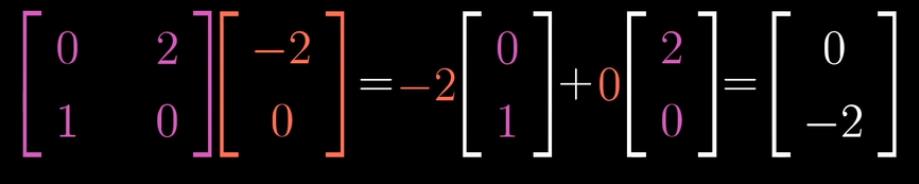
就算出了结果,且推论出矩阵公式。
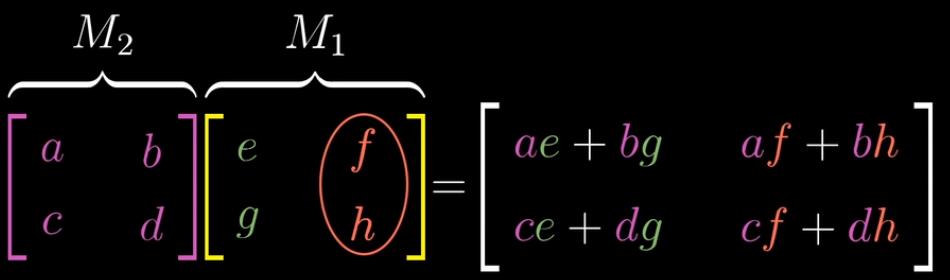
值得注意的是矩阵乘法不满足交换律,想象一下,先进行坐标系逆时针旋转90度的线性变换,然后剪切变换(1,0)(1,1),和先执行剪切变换后逆时针旋转的结果不同,基向量之间的夹角分别是锐角和钝角。

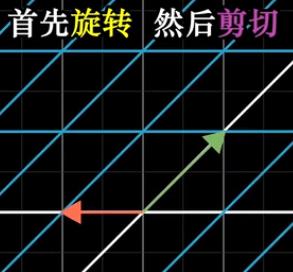
但是矩阵乘法是满足结合律的
想象一下,对一个向量旋转和缩放,然后剪切与先旋转,然后缩放剪切完全没有区别,根本不需要证明。
拓展到三维矩阵乘法
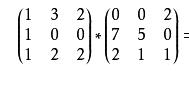
第一组基向量(0,7,2)执行变换,0*(1,1,1)+7*(3,0,2)+2*(2,0,2)就能得到结果的第一列基向量(25,0,18)
4.行列式求值
行列式求值,描述的是经历线性变换后,面积或者体积(二维和三维)的缩放系数首先不经历线性变换,两个单位基向量组成的区域为1,经历矩阵变换后,组成区域的面积就发生了变换,将矩阵写成行列式的形式,求出的值即为线性空间整体的面积缩放。有时候行列式求出的值是0,表示,矩阵的变换的列向量之间必然是线性相关的。让面积蜷缩到了一条线上。有时候行列式求出的值是负数,表示面的朝向发生了变化。
拓展到三维空间中,行列式的值可以看做单位正方体经历线性变换后的平行六面体的体积。行列式为负数,则空间取向翻转了,违反了右手定则,详见 Av6179111,只有方阵才有行列式。
行列式求值的话,几何意义如下,(a,0)和(0,d)构成的区域为长方形,可以直接算作ad。
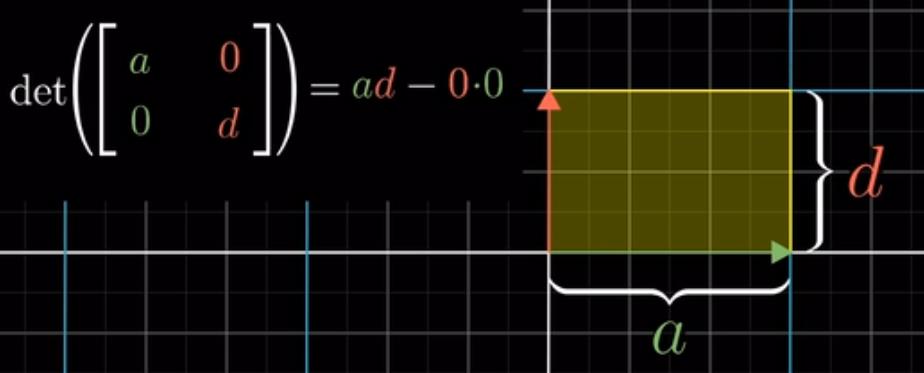
b,c任意一项为0的话,由于组成的是平行四边形,所以还是ad
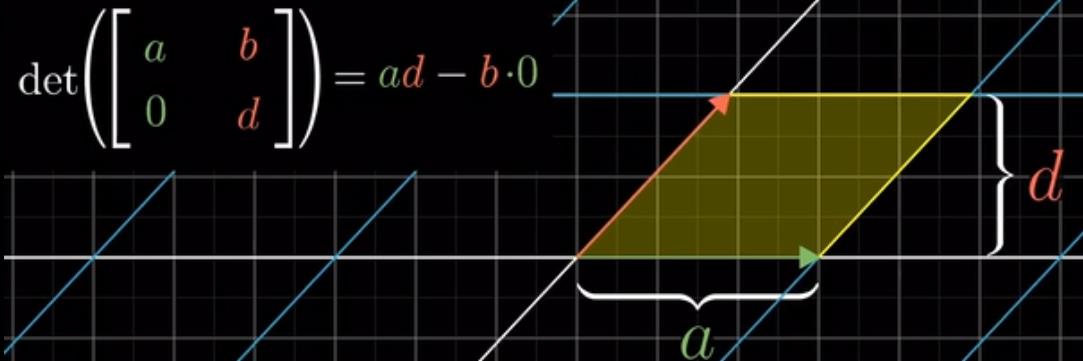
b,c都不为0,就需要靠这张简图了。最终结果精简为ad-bc
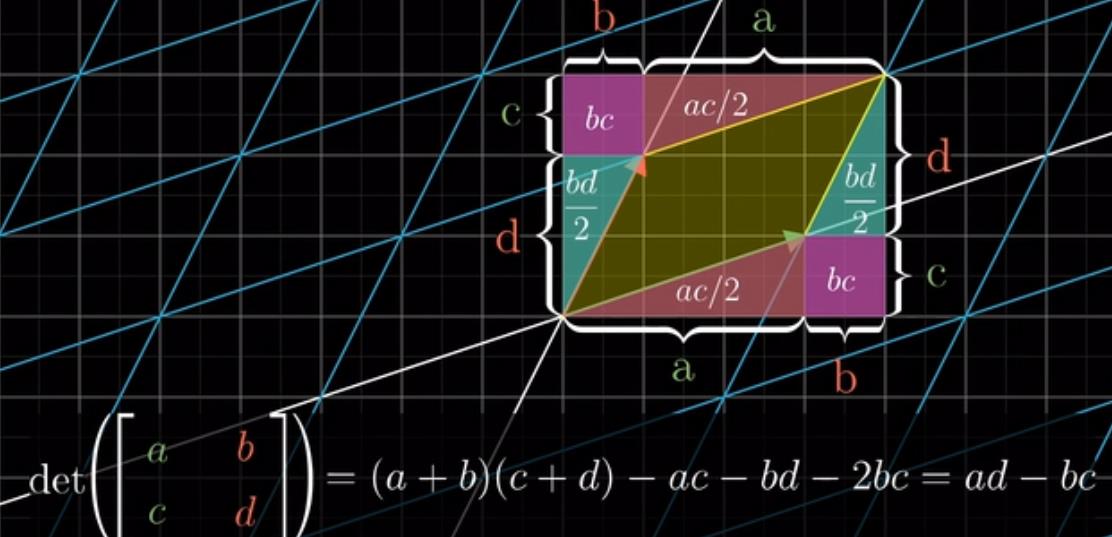
由此还可以推论,两个矩阵的行列式的值的乘积等于其复合矩阵的行列式的积。经历变换后面积还是相同的。
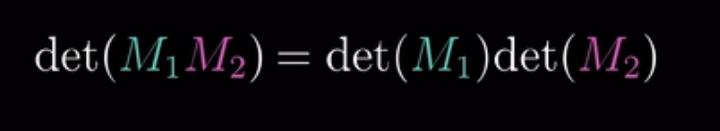
5.线性方程组
线性方程组到矩阵的转换图
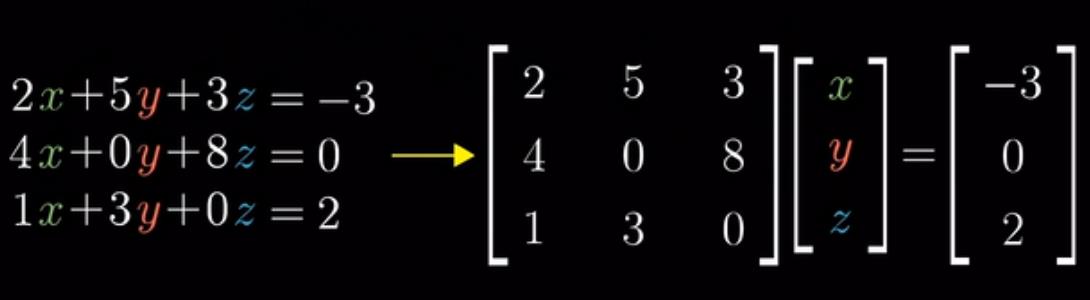
几何意义:已知经历矩阵转换后的向量(-3,0,2)和矩阵,求转换之前的未知向量(x,y,z)
这样只要将矩阵变换反过来就行了,也就是需要求出矩阵的逆,并与转换后的向量(-3,0,2)相乘,就能得到转换之前的未知向量(x,y,z)
为什么矩阵乘以矩阵的逆的结果是单位矩阵?因为先进行一次矩阵变换,再逆回去,相当于什么都不做。那么基向量还是(1,0)和(0,1)也就是所谓的单位矩阵。
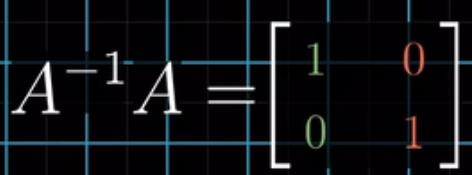
之前说过行列式值如果为0,二维空间就可能被压缩到一条线上,这种情况下,即使给定转换后的向量,也无法求出之前的向量(相当于有无数的解与之对应)。相当于你不能将一条线解压缩到一个平面,所以行列式的值为0的话,矩阵就不存在逆。
拿三维矩阵举例,矩阵的三个基向量最大可以展开空间到三维,也有可能压缩到二维空间(面)或者一维空间(线)中。这个就是矩阵的秩,代表当前矩阵能展开到几维空间。
6.列空间:
对于任意向量而言,矩阵对其变换后的所有解可能是一个空间,或者一个面,或者一条线,对矩阵来说,所有可能的输出向量构成的集合就是矩阵的列空间。所以矩阵的秩相当于其列空间的维数。之所以叫做列空间,是因为矩阵本身每列都是变换后的基向量,所有解本质是基向量的组合。由于矩阵展开的维度是由其列向量中线性无关的数量决定的,也可以用此来求秩。
零向量一定在列空间中,因为原点不变,(0,0)变换后还是(0,0)。在满秩变换中,每个解都有唯一的原向量与之对应。非满秩的情况下,有其他向量会被压缩到零向量里,
在变换后落在原点的原向量集合被称为这个矩阵的零空间或核。
7.非方阵的几何意义
对于3*2的矩阵,可以理解为输入2个基向量,但是变换后的基向量是用三个独立的坐标来描述的,解的维度还是平面,只不过是用空间中的向量坐标去表示这个平面了。将二维空间映射到三维空间上。
需要注意的是,这个矩阵仍然是满秩的,因为,原向量是二维,输出向量还是二维且一一对应,所以是满秩。
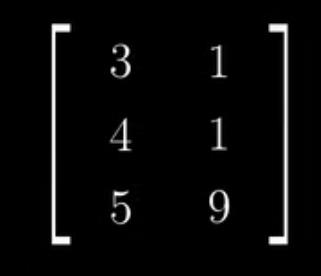
对于2*3的矩阵,原始空间的基向量有3个,但变换后只用两个坐标去描述它,相当于三维空间在二维坐标系上的投影。
(此矩阵的秩应为2,因为输入是3 个基向量,输出是投影到2维空间的)

7.点积
例如:向量(1,2)和向量(3,4)的乘积可以转换为下图,向量可以视作一维矩阵(就像基向量一样,x写在上面,y写在下面)
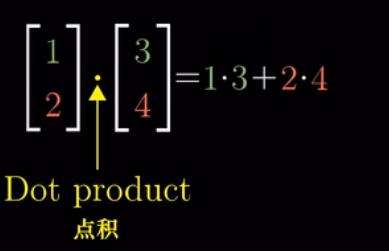
得出公式1:
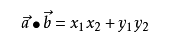
公式2:通常用来算夹角,将两个向量归一化之后,通过点积可以直接算出cosa的值。例如60度0.5,90度0
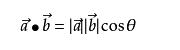
8.叉积
在二维空间中,叉积算出的向量的模实际是在计算两个向量的面积,例如(3,1)和(2,-1)的叉积,可以视作接通过计算两个基向量组成矩阵的面积,从而算其行列式的模。

叉积算垂直于2个向量平面的第三个向量符合右手定则,叉积方向由此确定。
如图所示,叉积的长度是v和w组成的面积。
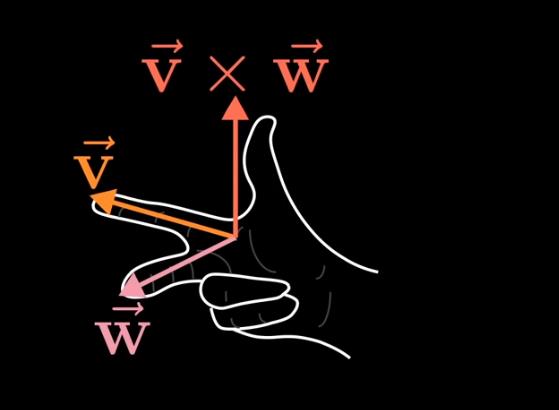
补充:这个是标准坐标系,绿色是x,j红色是y,蓝色是z
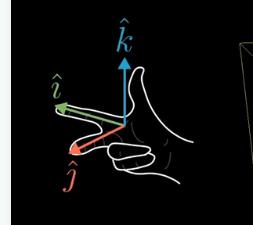
拓展到三维,叉积可以按照行列式的计算方法去推导叉积的计算公式
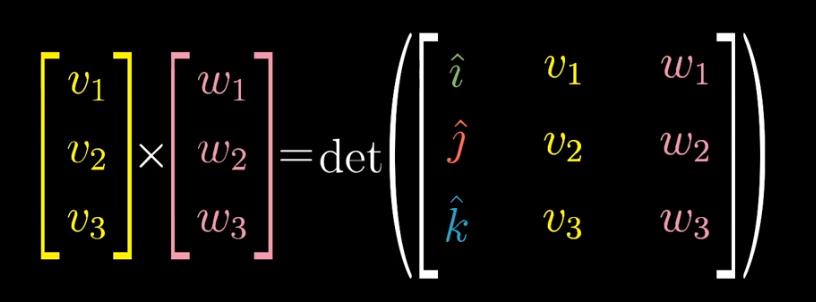
9.基变换
如果以矩阵转换后的空间作为坐标系,我们可以通过矩阵得知该坐标系的基向量的坐标。
(2,1)(-1,1)。

那么在该新的坐标系中,(-1,2)所代表的向量的含义是什么,怎么转换到标准坐标系?
含义就是-1*基向量i+2*基向量j。在它的坐标系中基向量i是(1,0),基向量j是(0.1)。
但由转换矩阵可知在标准坐标系中,它的基向量是(2,1)和(-1,1)。,所以由此可以算出矩阵转换后坐标系(-1,2)在标准坐标系中的坐标(-4,1)。
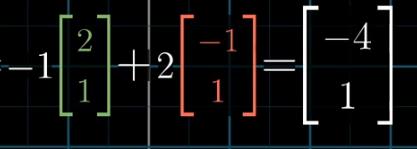
会发现这其实是矩阵和向量的乘法。但是经常给人带来错觉,感觉上这个矩阵是将标准坐标系变换为其它坐标系,这个式子好像是将标准坐标系下的向量(-1,2)线性转换到新的坐标系下,看看新坐标是什么?
实际不是,这里应该将(-1,2)单纯看作是坐标系中对基向量的组合系数,给出基向量组合系数,再给出当前所谓的基向量(即矩阵),就能知道在标准坐标系下,这个(-1,2)的坐标到底是什么。
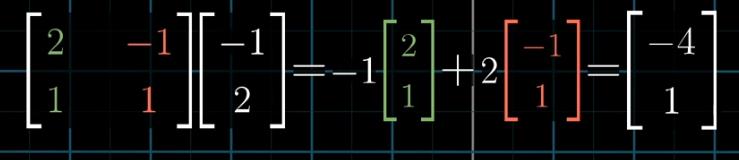
那么如果是标准坐标系下的坐标(如(3,2),给定矩阵的基向量,想知道在这组基向量下,所描述的坐标是多少?
仔细回想一下,之前求线性方程组解的时候,提到了已知转换后的的在标准坐标系下的向量(3,2),求在某组基向量下的未知向量。只需要此向量乘以矩阵的逆即可。
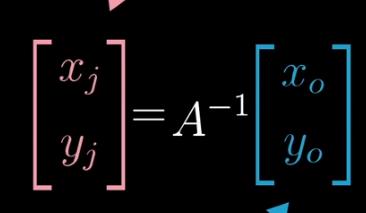
那么如果在标准坐标系下的旋转矩阵,用变换后的矩阵所在的线性空间来描述,该怎么描述?比如旋转矩阵。
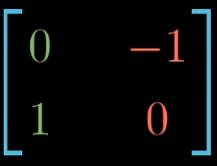
首先如图所示,还是从右往左读,先对空间按矩阵进行一次变换,然后进行旋转了,得到了复合矩阵。然后再乘以此矩阵的逆,就是在此矩阵空间下描述的旋转矩阵。
输入一个用此矩阵空间描述的向量,与等式右端的矩阵相乘,输出的向量就是在此空间下旋转了90度的向量(还是用此空间描述)。
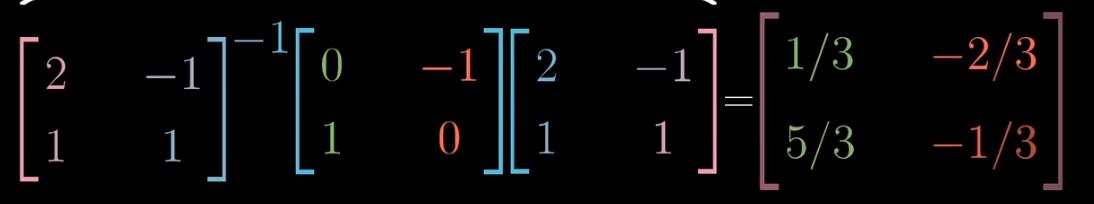
还可以推出如下的表达式。注意矩阵乘法不满足交换律,所以A的逆不能和A先合并成单位矩阵。

10.特征值
在进行线性变换时,有时会存在一条线上的点并不随此变换而偏离其所在的线,这些向量叫做矩阵变换的特征向量,例如坐标的伸缩程度(1,1)到(2,2)为2,叫做该矩阵的特征值。
例如旋转矩阵,如果你找到这么一条线,实际上就是找到了它的旋转轴。但是旋转不缩放任何一个向量,所以特征值为1。(av6540378)
11.抽象向量空间
在线性空间内,函数也可以看做向量,其满足相加性和成比例。(函数的求导也是线性运算)那么对于一个函数来说,其也存在对应的基向量——基函数。任意一个向量可以看作基向量的线性组合,函数也可以看作基函数的线性组合。
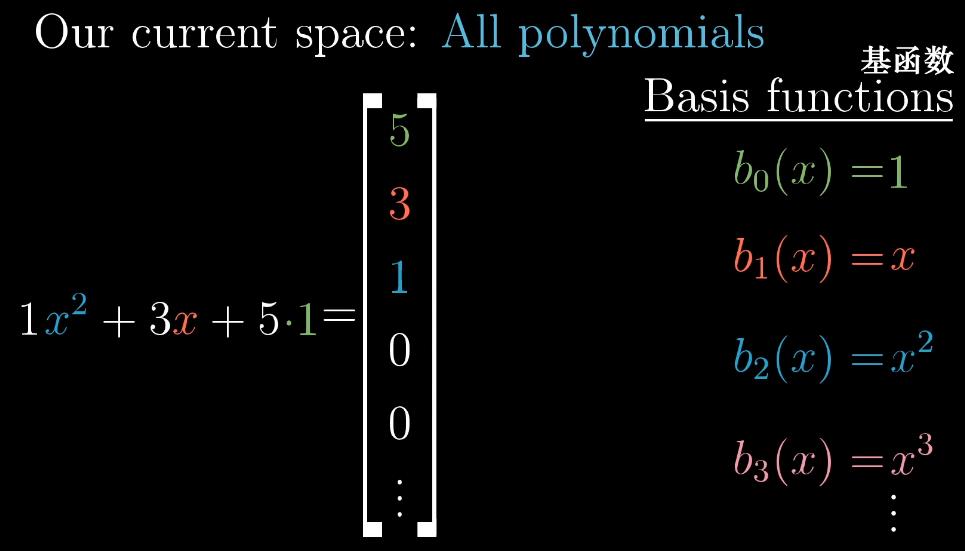
举例来说:求导函数可以视作矩阵转换,对某函数求导,相当于对一个向量进行矩阵变换。如下所示。左边的求导矩阵是将4个基函数每个进行求导得到新基函数组成的矩阵。结果得出了转换后的向量(0,4,10,3)
