LeedCode第 244 场周赛（二）

5776. 判断矩阵经轮转后是否一致

题目链接：https://leetcode-cn.com/problems/determine-whether-matrix-can-be-obtained-by-rotation/

给你两个大小为 n x n 的二进制矩阵 mat 和 target 。现 以 90 度顺时针轮转 矩阵 mat 中的元素 若干次 ，如果能够使 mat 与 target 一致，返回 true ；否则，返回 false 。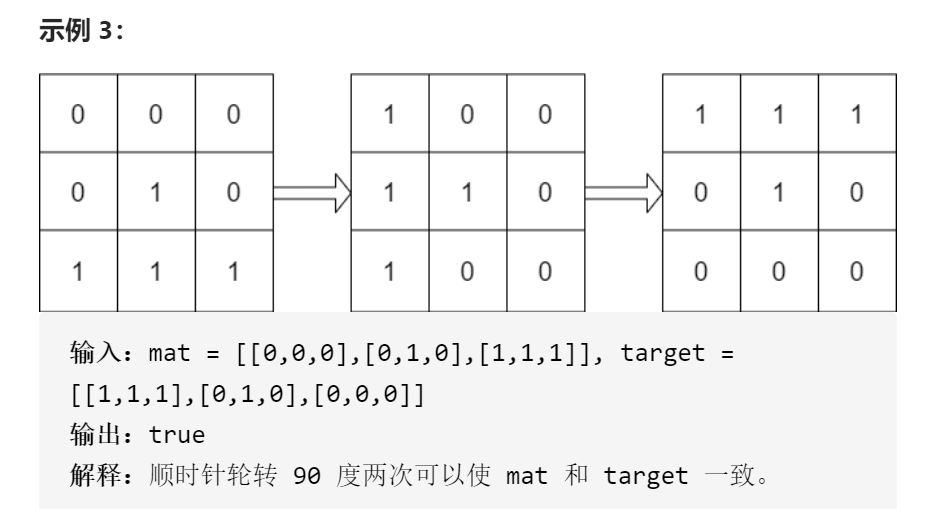

 题目思路：

主要给出转换过程中每个点的横纵坐标的变化表示，比如，设置矩阵中任意一点A的坐标是（i ,j），则顺时针旋转90度后的坐标是(j , n-1-i），继续顺时针旋转90度后的坐标是（n-1-i.n-1-j），接着再顺时针选择90度后的坐标是（n-1-j , i），最后顺时针旋转90度后，回到起点（i ，j）。

C++代码：

class Solution {
public:
    bool findRotation(vector<vector<int>>& mat, vector<vector<int>>& target) {
        int n = mat.size();
        int m = target.size();
        int sum=0;
        int sum1=0;
        int sum2=0;
        int sum3=0;
        if(m==n)
        {
            for(int i=0; i<n ;i++)
            {
                for(int j=0 ;j<n; j++)
                {
                    if(mat[i][j]==target[i][j])
                    {   
                       // printf("%d %d
",i,j);
                        sum++;
                    }
                }
            }
            
          for(int i=0; i<n ;i++)
            {
                for(int j=0 ;j<n; j++)
                {
                    if(mat[i][j]==target[j][n-1-i])
                    {   
                       // printf("%d %d
",i,j);
                        sum1++;
                    }
                }
            }
            
            for(int i=0; i<n ;i++)
            {
                for(int j=0 ;j<n; j++)
                {
                    if(mat[i][j]==target[n-1-i][n-1-j])
                    {   
                       // printf("%d %d
",i,j);
                        sum2++;
                    }
                }
            }
            
             for(int i=0; i<n ;i++)
            {
                for(int j=0 ;j<n; j++)
                {
                    if(mat[i][j]==target[n-1-j][i])
                    {   
                       // printf("%d %d
",i,j);
                        sum3++;
                    }
                }
            }
     
            //if(sum2==sum3)
           // printf("sxiangtong %d %d
",sum2,sum3);
            int ans=n*n;
          //  printf("sum : %d ans: %d
",sum,ans);
            if((sum==ans) || (sum1==ans) || (sum2==ans) || (sum3==ans))
            {
               return true;
            }
            else
            {
              return false;
            }
        }
           
        else 
            return false;
    }
};

 

5777. 使数组元素相等的减少操作次数

题目链接：https://leetcode-cn.com/problems/reduction-operations-to-make-the-array-elements-equal/

给你一个整数数组 nums ，你的目标是令 nums 中的所有元素相等。完成一次减少操作需要遵照下面的几个步骤：

找出 nums 中的 最大 值。记这个值为 largest 并取其下标 i （下标从 0 开始计数）。如果有多个元素都是最大值，则取最小的 i 。
找出 nums 中的 下一个最大 值，这个值 严格小于 largest ，记为 nextLargest 。
将 nums[i] 减少到 nextLargest 。
返回使 nums 中的所有元素相等的操作次数。

 解题思路：

先sort快排，然后采用前缀的思想，也可以理解为后一个数值和相邻的前一个数值有关，并把操作的次数记录下来。

C++代码：

class Solution {
public:
    int reductionOperations(vector<int>& nums) {
        int n=nums.size();
        int ans=0;
        int sum[50005];
        memset(sum, 0, sizeof(sum));
        sort(nums.begin(),nums.end());
        for(int i=0;i<n-1;i++)
        {
            if(nums[i+1]!=nums[i])
            {
                sum[i+1]=sum[i]+1;
            }
            else
            {
                sum[i+1]=sum[i];
            }
        }
        for(int i=0 ; i<n ; i++)
        {
            ans = ans + sum[i];
        }
        return ans;
    }
};

5778. 使二进制字符串字符交替的最少反转次数

题目链接：https://leetcode-cn.com/problems/minimum-number-of-flips-to-make-the-binary-string-alternating/

给你一个二进制字符串 s 。你可以按任意顺序执行以下两种操作任意次：

类型 1 ：删除 字符串 s 的第一个字符并将它 添加 到字符串结尾。
类型 2 ：选择 字符串 s 中任意一个字符并将该字符 反转 ，也就是如果值为 '0' ，则反转得到 '1' ，反之亦然。
请你返回使 s 变成 交替 字符串的前提下， 类型 2 的 最少 操作次数 。

我们称一个字符串是 交替 的，需要满足任意相邻字符都不同。

比方说，字符串 "010" 和 "1010" 都是交替的，但是字符串 "0100" 不是。

 解题思路1：

滑动窗口的方法。

对字符串 s 变成2倍的s。

然后我们用01和10交替创建两个相同长度的不同字符串。例如：s =11100

• • s = 1110011100
  • s1 = 1010101010
  • s2= 0101010101
• 最后，使用滑动窗口（大小 n）将 s 与 s1 和 s2 进行比较。
• 为什么我们可以将 s 加倍来完成第一个操作，让我们看一下相同的示例 s = 11100:`
  • 双 s： 1110011100
  • 大小为n的窗口: |11100|11100 ==> 1|11001|1100 ==> 11|10011|100 以此类推，当我们移动滑动窗口一步时，同样从头开始追加1个元素。

参考链接：https://leetcode.com/problems/minimum-number-of-flips-to-make-the-binary-string-alternating/discuss/1253874/C++-Solution-sliding-window.-O(N)

C++代码：

class Solution {
public:
    int minFlips(string s) {
        int n = s.size();
        s += s;
        string s1, s2;
        
        for(int i = 0; i < s.size(); i++) {
            s1 += i % 2 ? '0' : '1';
            s2 += i % 2 ? '1' : '0';
        }
        int ans1 = 0, ans2 = 0, ans = INT_MAX;
        for(int i = 0; i < s.size(); i++) {
            if(s1[i] != s[i]) ++ans1;
            if(s2[i] != s[i]) ++ans2;
            if(i >= n) { //the most left element is outside of sliding window, we need to subtract the ans if we did `flip` before.
                if(s1[i - n] != s[i - n]) --ans1;
                if(s2[i - n] != s[i - n]) --ans2;
            }
            if(i >= n - 1)
                ans = min({ans1, ans2, ans});
        }
        return ans;
    }
};

解题思路2：

分析+前缀和+后缀和

提示 1
我们可以将所有类型 2的操作安排在类型 1 的操作之前。
提示 1 解释
由于类型 2 的操作是反转任意一个字符，而类型 1 的操作只会改变字符的相对顺序，不会改变字符的值。因此如果我们想要修改某个字符，随时都可以修改。这样我们就可以把所有类型 2 的操作安排到最前面。
提示 2
设字符串 ss 的长度为 n。

如果 n 是偶数，那么在所有类型 2 的操作完成后，s 已经是一个交替字符串了。

提示 2 解释

当 n 是偶数时，交替字符串只可能为 010101⋯01 或者101010⋯10 的形式。对这两个字符串进行类型 2 的操作，只会在它们之间相互转换。

类型 2 的操作是可逆的，这说明交替字符串只可能由交替字符串通过类型 2 的操作得来。因此，在所有类型 2 的操作完成后，s 必须是一个交替字符串。

提示 3

如果 n 是奇数，那么交替字符串为 0100101⋯010 或者 1011010⋯101 的形式。

我们首先考虑 0100101⋯010，如果在所有类型 2 的操作完成后，s 可以通过类型 2 的操作得到该字符串，那么：

要么 s 就是 0100101⋯010；

要么 s 是  0101⋯010∣01⋯01 的形式，或者是  01010⋯10∣01⋯010 的形式。这里我们用竖线 | 标注了类型 2 的操作，在 | 左侧的字符通过类型 2 的操作被移动到字符串的末尾，最终可以得到 0100101⋯010。

因此，s 要么是一个交替字符串（即  0100101⋯010），要么由两个交替字符串拼接而成，其中左侧的交替字符串以 0 结尾，右侧的交替字符串以 0 开头。

同理，如果我们考虑  1011010⋯101，那么 s 要么就是 1011010⋯101，要么由两个交替字符串拼接而成，其中左侧的交替字符串以 1 结尾，右侧的交替字符串以 1 开头。


我们用pre[i][j] 表示对于字符串的前缀 s[0..i]s[0..i]，如果我们希望通过类型 2 的操作修改成「以 j 结尾的交替字符串」，那么最少需要的操作次数。这里 j 的取值为 0 或 1。根据定义，有递推式：
pre[i][0]=pre[i−1][1]+I(s[i],1)
pre[i][1]=pre[i−1][0]+I(s[i],0)


其中 I(x,y) 为示性函数，如果 x=y，那么函数值为 1，否则为 0。例如 I(s[i],1) 就表示：如果s[i] 为 1，那么我们需要通过类型 2 的操作将其修改为 0，否则无需操作。

同理，我们用suf[i][j] 表示对于字符串的后缀 s[0..i]s[0..i]，如果我们希望通过类型 2 的操作修改成「以 j 开头的交替字符串」，那么最少需要的操作次数。这里 j 的取值为 0 或 1，同样有递推式：
suf[i][0]=suf[i+1][1]+I(s[i],1)
suf[i][1]=suf[i+1][0]+I(s[i],0)

在求解完数组 pre 和suf 后：

答案可以为 pre[n−1][0] 或者 pre[n−1][1]，对应着将 s 本身变为一个交替字符串；

如果 n 是奇数，那么答案还可以为 pre[i][0]+suf[i+1][0] 以及pre[i][1]+suf[i+1][1]，对应着将 s 变为两个交替字符串的拼接。

所有可供选择的答案中的最小值即为类型 2 的操作的最少次数。

细节：如果 n 是偶数，我们无需求出 suf 。

参考链接：https://leetcode-cn.com/problems/minimum-number-of-flips-to-make-the-binary-string-alternating/solution/shi-er-jin-zhi-zi-fu-chuan-zi-fu-jiao-ti-i52p/

C++代码：

class Solution {
public:
    int minFlips(string s) {
        //示性函数
        auto I = [](char ch, int x) -> int {
            return ch - '0' == x;
        };

        int n = s.size();
        vector<vector<int>> pre(n, vector<int>(2));

        //注意 i=0 的边界情况
        for(int i=0 ; i<n ;++i)
        {
            pre[i][0]=(i==0 ? 0 : pre[i-1][1])+I(s[i],1);
            pre[i][1]=(i==0 ? 0 : pre[i-1][0])+I(s[i],0);
        }
        int ans = min(pre[n - 1][0], pre[n - 1][1]);

        //如果n是奇数，还需要求出suf
        if (n % 2 == 1) {
            // 如果 n 是奇数，还需要求出 suf
            vector<vector<int>> suf(n, vector<int>(2));
            // 注意 i=n-1 的边界情况
            for (int i = n - 1; i >= 0; --i) {
                suf[i][0] = (i == n - 1 ? 0 : suf[i + 1][1]) + I(s[i], 1);
                suf[i][1] = (i == n - 1 ? 0 : suf[i + 1][0]) + I(s[i], 0);
            }
            for (int i = 0; i + 1 < n; ++i) {
                ans = min(ans, pre[i][0] + suf[i + 1][0]);
                ans = min(ans, pre[i][1] + suf[i + 1][1]);
            }
        }

        return ans;
    }
};