十大经典排序算法

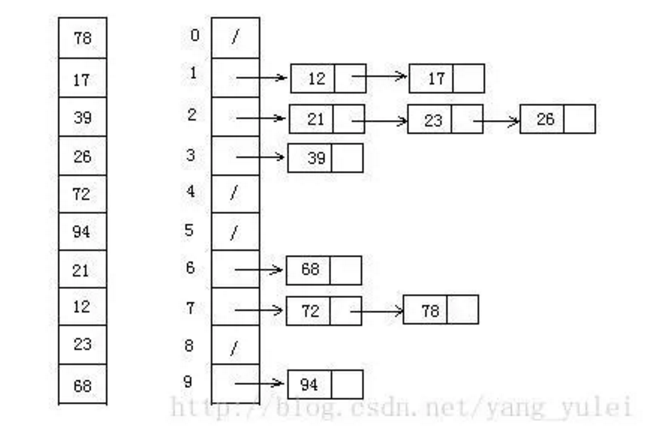
0.1 排序的定义

对一序列对象根据某个关键字进行排序。

0.2 术语说明

• 稳定：如果a原本在b前面，而a=b，排序之后a仍然在b的前面；

• 不稳定：如果a原本在b的前面，而a=b，排序之后a可能会出现在b的后面；

• 内排序：所有排序操作都在内存中完成；

• 外排序：由于数据太大，因此把数据放在磁盘中，而排序通过磁盘和内存的数据传输才能进行；

• 时间复杂度：一个算法执行所耗费的时间。

• 空间复杂度：运行完一个程序所需内存的大小。                                                                                                                                                                                         

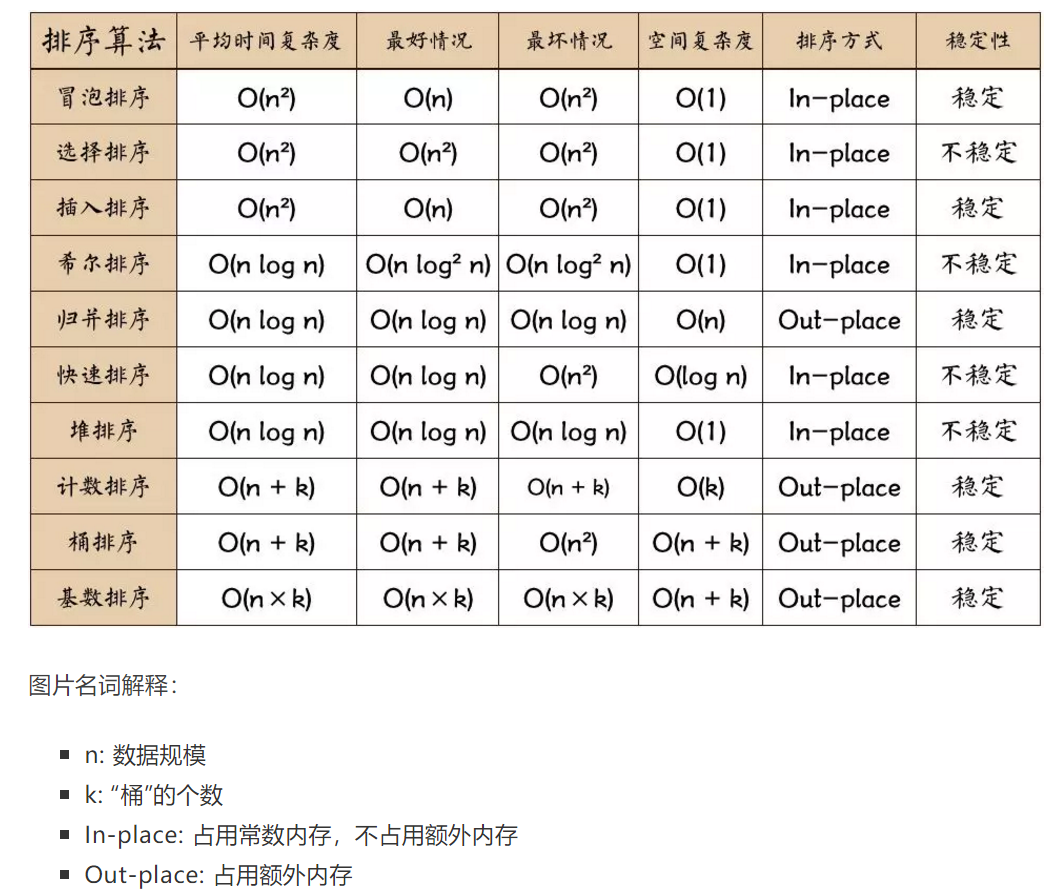
  0.3 算法总结

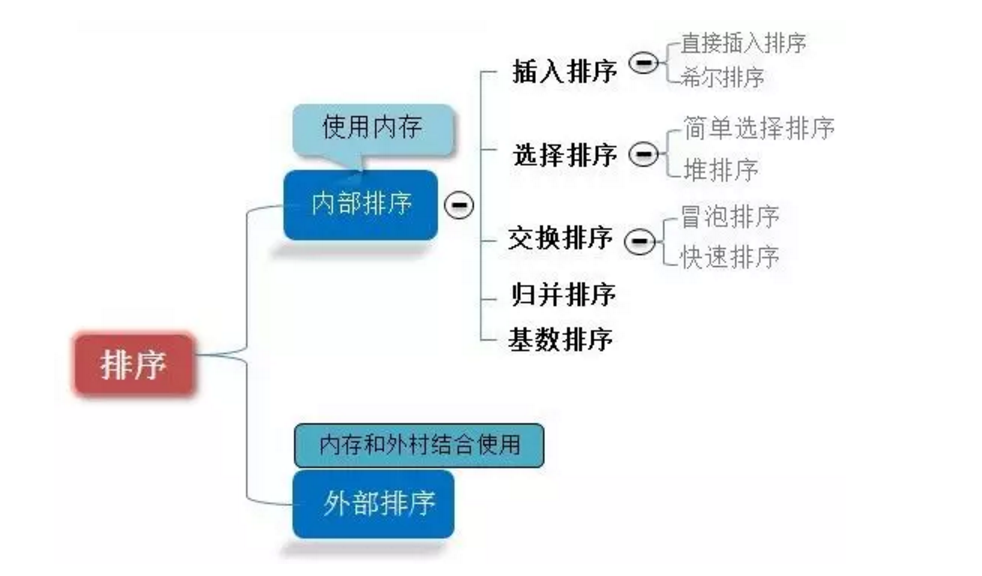
  0.4 算法分类

1、冒泡排序（Bubble Sort）

冒泡排序是一种简单的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。

这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。冒泡排序介绍：冒泡排序

1.1 算法描述

• 比较相邻的元素。如果第一个比第二个大，就交换它们两个；

• 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对，这样在最后的元素应该会是最大的数；

• 针对所有的元素重复以上的步骤，除了最后一个；

• 重复步骤1~3，直到排序完成。                                                                                                                                                                                                                   

  代码实现

  

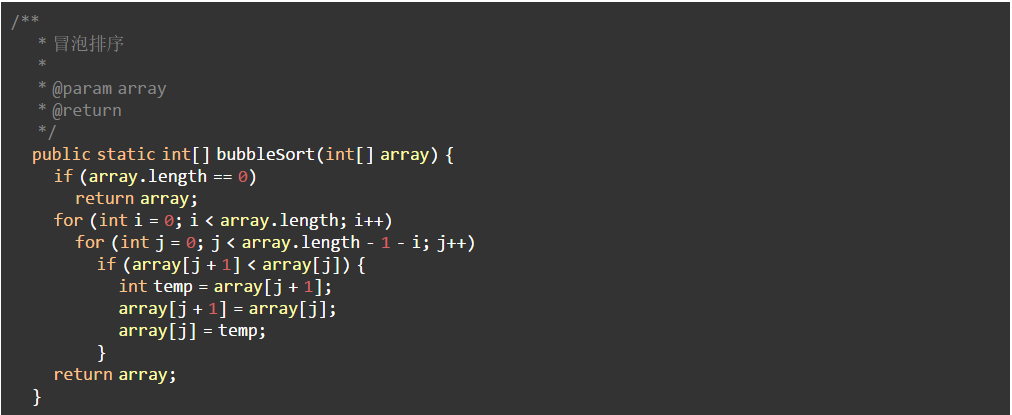
  2、选择排序（Selection Sort）

• 2.1 算法描述

  n个记录的直接选择排序可经过n-1趟直接选择排序得到有序结果。具体算法描述如下：

  • 初始状态：无序区为R[1..n]，有序区为空；

  • 第i趟排序(i=1,2,3…n-1)开始时，当前有序区和无序区分别为R[1..i-1]和R(i..n）。该趟排序从当前无序区中-选出关键字最小的记录 R[k]，将它与无序区的第1个记录R交换，使R[1..i]和R[i+1..n)分别变为记录个数增加1个的新有序区和记录个数减少1个的新无序区；

  • n-1趟结束，数组有序化了。                                                                                                                                                                                                         

    2.3 代码实现   

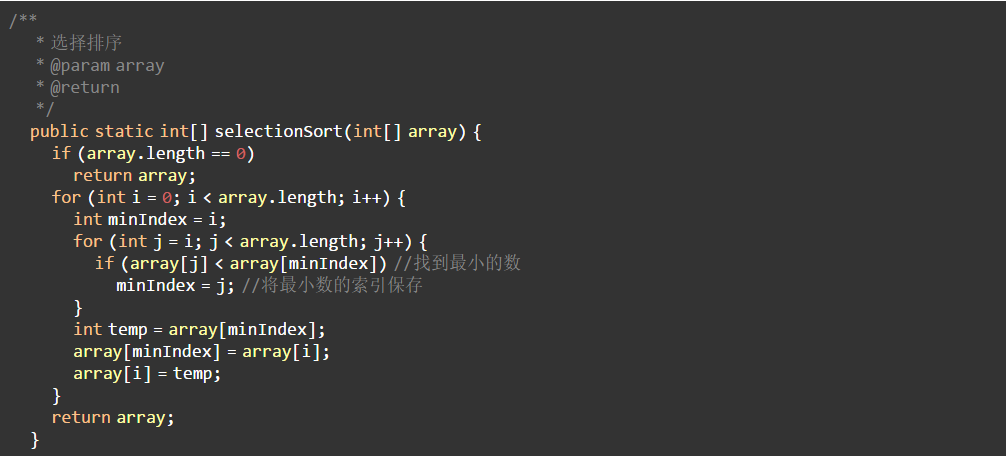
    3、插入排序（Insertion Sort）

    3.1 算法描述

    一般来说，插入排序都采用in-place在数组上实现。具体算法描述如下：

    • 从第一个元素开始，该元素可以认为已经被排序；

    • 取出下一个元素，在已经排序的元素序列中从后向前扫描；

    • 如果该元素（已排序）大于新元素，将该元素移到下一位置；

    • 重复步骤3，直到找到已排序的元素小于或者等于新元素的位置；

    • 将新元素插入到该位置后；

    • 重复步骤2~5。

      3.2 代码实现

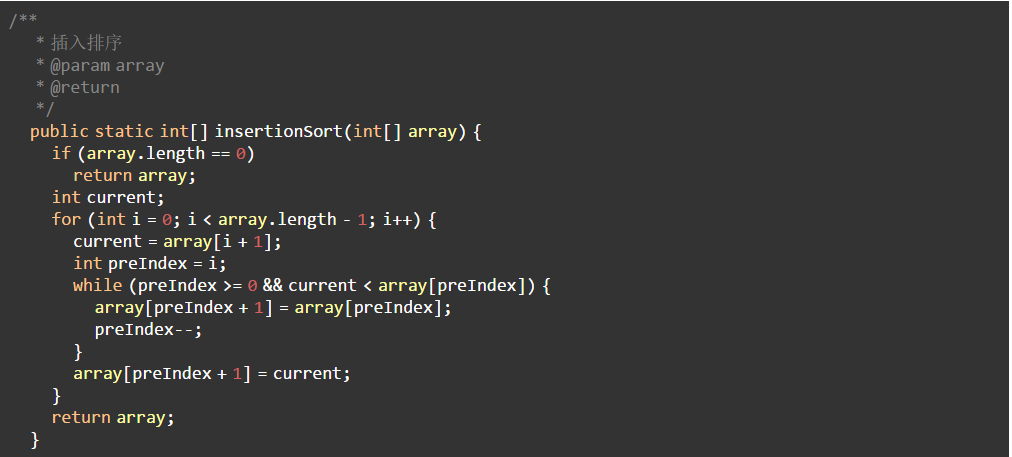
      4、希尔排序（Shell Sort）

      4.1 算法描述

      我们来看下希尔排序的基本步骤，在此我们选择增量gap=length/2，缩小增量继续以gap = gap/2的方式，这种增量选择我们可以用一个序列来表示，{n/2,(n/2)/2…1}，称为增量序列。希尔排序的增量序列的选择与证明是个数学难题，我们选择的这个增量序列是比较常用的，也是希尔建议的增量，称为希尔增量，但其实这个增量序列不是最优的。此处我们做示例使用希尔增量。

      先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序，具体算法描述：

      • 选择一个增量序列t1，t2，…，tk，其中ti>tj，tk=1；

      • 按增量序列个数k，对序列进行k 趟排序；

      • 每趟排序，根据对应的增量ti，将待排序列分割成若干长度为m 的子序列，分别对各子表进行直接插入排序。仅增量因子为1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。

        4.2 过程演示

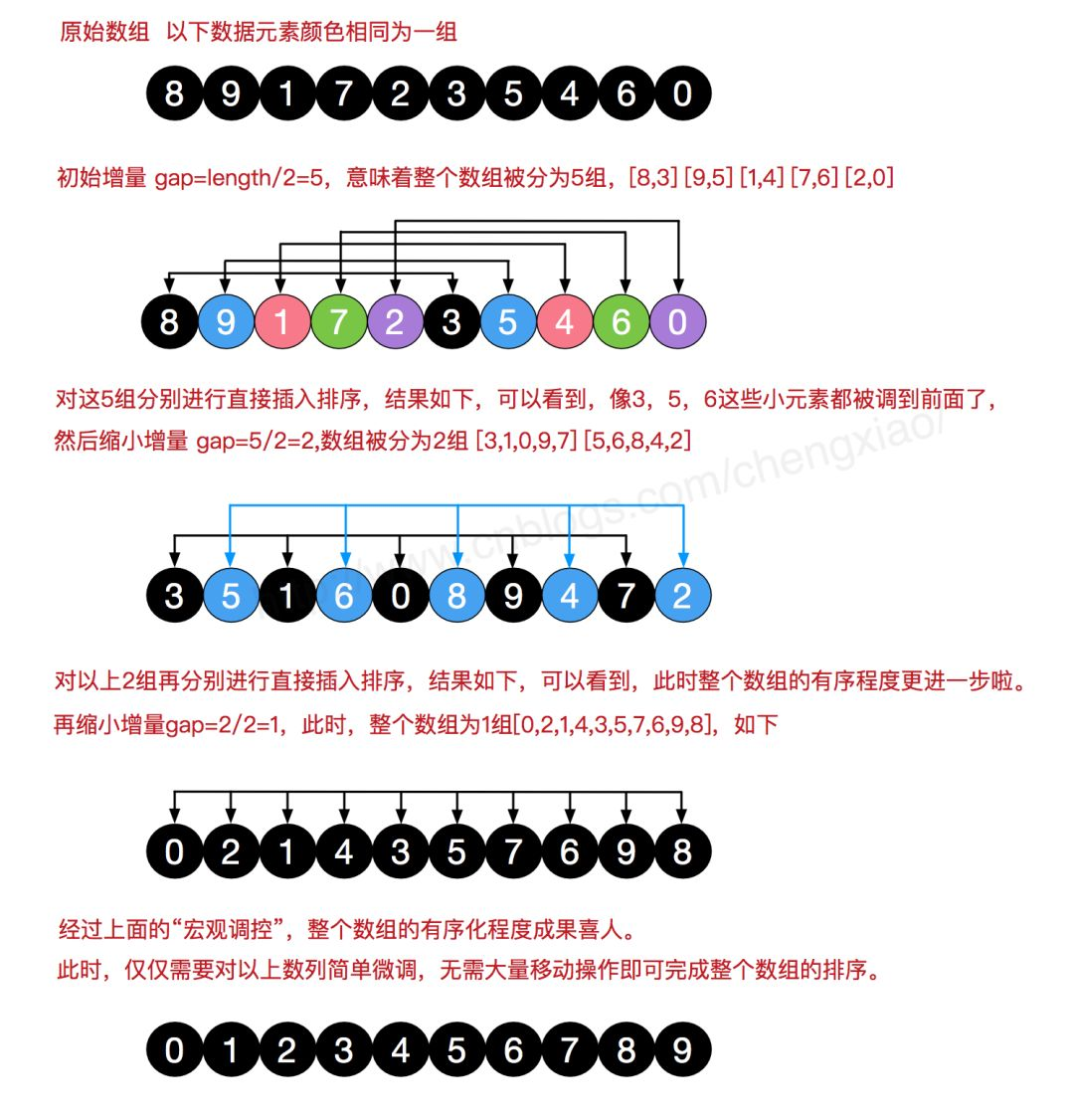
        4.3 代码实现

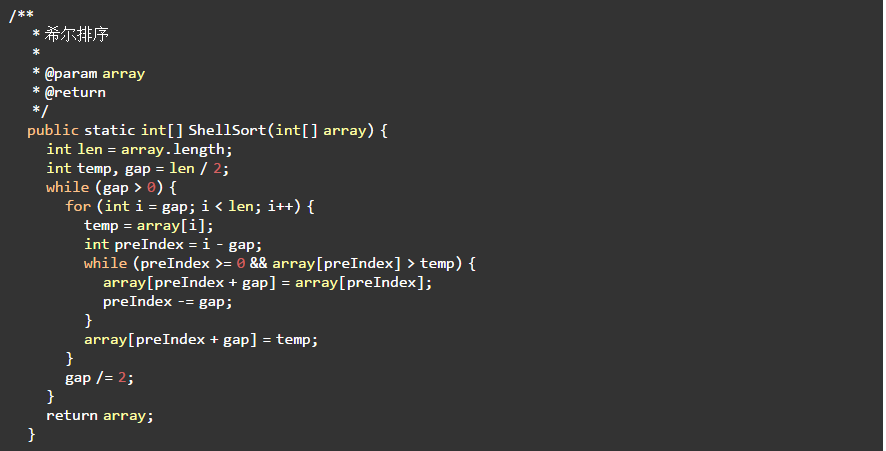
        5、归并排序（Merge Sort）

        5.1 算法描述

        • 把长度为n的输入序列分成两个长度为n/2的子序列；

        • 对这两个子序列分别采用归并排序；

        • 将两个排序好的子序列合并成一个最终的排序序列。

          5.2代码实现

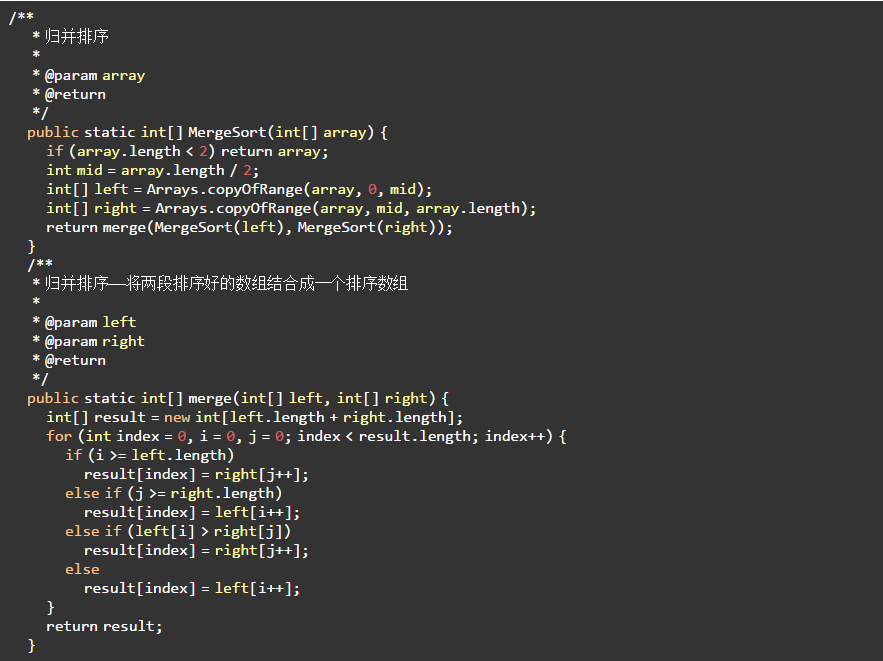
          6、快速排序（Quick Sort）

        6.1 算法描述

        快速排序使用分治法来把一个串（list）分为两个子串（sub-lists）。具体算法描述如下：

        • 从数列中挑出一个元素，称为 “基准”（pivot）；

        • 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；

        • 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

          6.2 代码实现

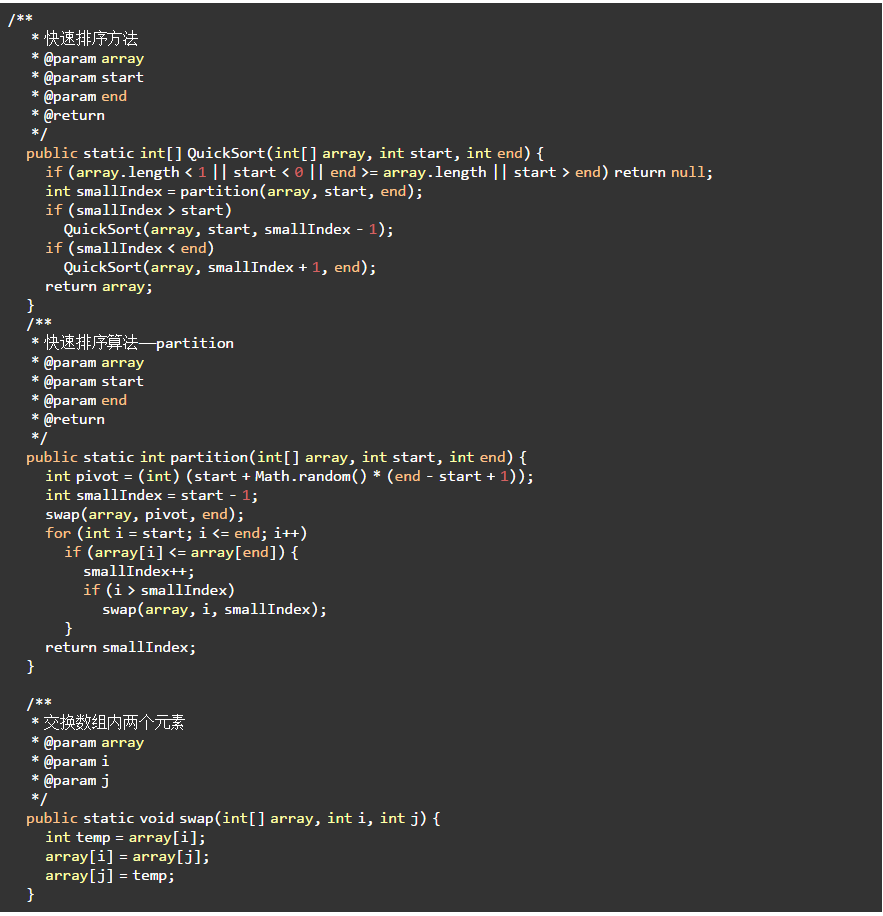
          7、堆排序（Heap Sort）

          7.1 算法描述

          • 将初始待排序关键字序列(R1,R2….Rn)构建成大顶堆，此堆为初始的无序区；

          • 将堆顶元素R[1]与最后一个元素R[n]交换，此时得到新的无序区(R1,R2,……Rn-1)和新的有序区(Rn),且满足R[1,2…n-1]<=R[n]；

          • 由于交换后新的堆顶R[1]可能违反堆的性质，因此需要对当前无序区(R1,R2,……Rn-1)调整为新堆，然后再次将R[1]与无序区最后一个元素交换，得到新的无序区(R1,R2….Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1，则整个排序过程完成。

            7.2 代码实现

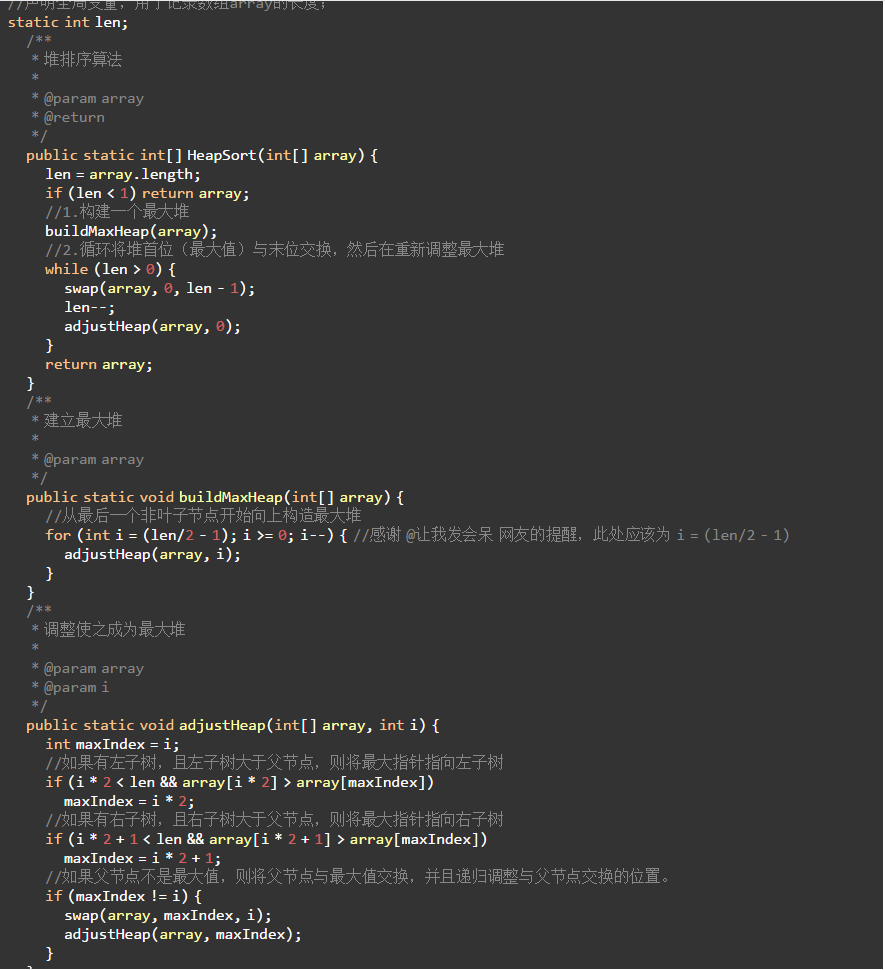
            8、计数排序（Counting Sort）

            8.1 算法描述

            • 找出待排序的数组中最大和最小的元素；

            • 统计数组中每个值为i的元素出现的次数，存入数组C的第i项；

            • 对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）；

            • 反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1。

              8.2 代码实现

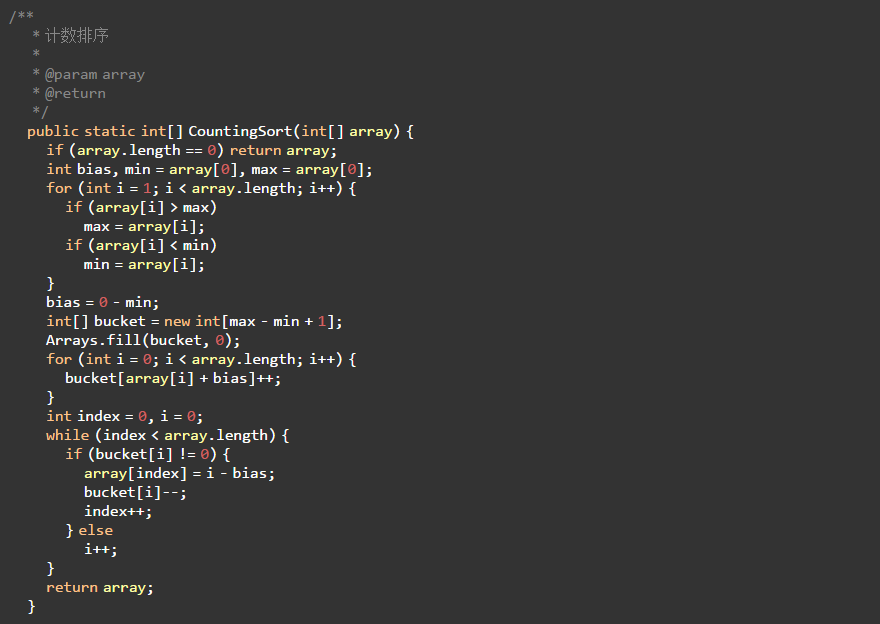
              9、桶排序（Bucket Sort）

              9.1 算法描述

              • 人为设置一个BucketSize，作为每个桶所能放置多少个不同数值（例如当BucketSize==5时，该桶可以存放｛1,2,3,4,5｝这几种数字，但是容量不限，即可以存放100个3）；

              • 遍历输入数据，并且把数据一个一个放到对应的桶里去；

              • 对每个不是空的桶进行排序，可以使用其它排序方法，也可以递归使用桶排序；

              • 从不是空的桶里把排好序的数据拼接起来。

              注意，如果递归使用桶排序为各个桶排序，则当桶数量为1时要手动减小BucketSize增加下一循环桶的数量，否则会陷入死

              循环，导致内存溢出。

              9.2 图片演示

            • 

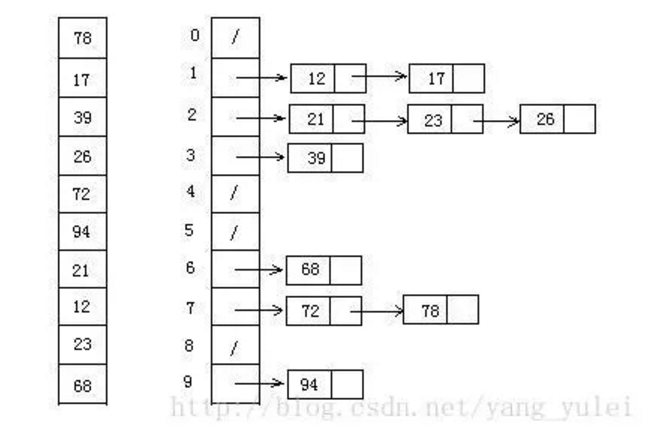
          9.3 代码实现

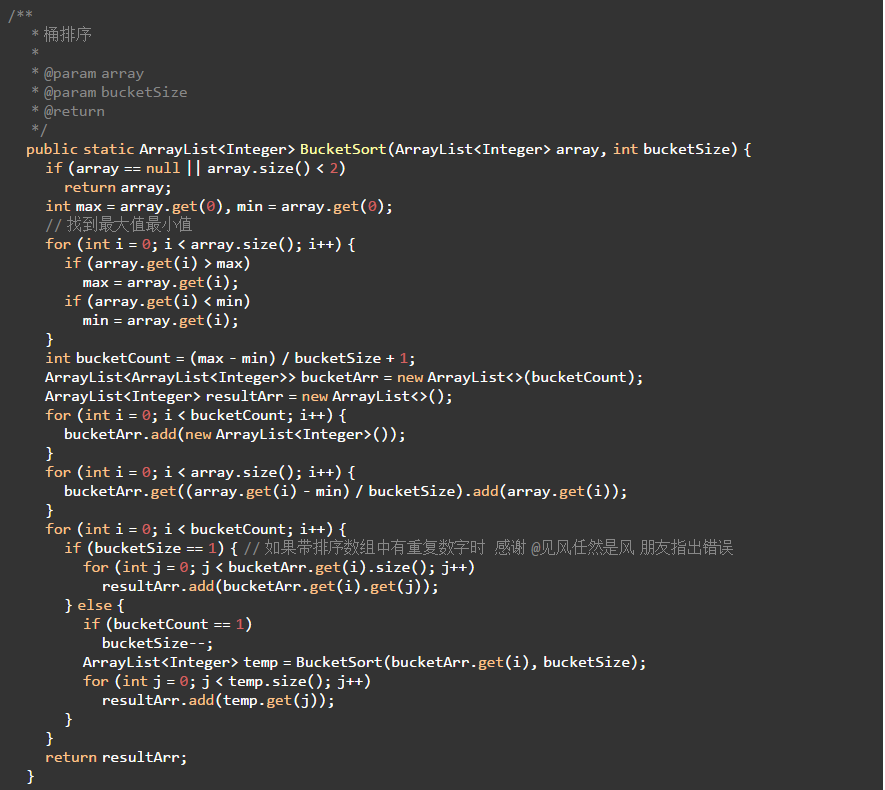
          10、基数排序（Radix Sort）

          10.1 算法描述

          • 取得数组中的最大数，并取得位数；

          • arr为原始数组，从最低位开始取每个位组成radix数组；

          • 对radix进行计数排序（利用计数排序适用于小范围数的特点）；

            10.2 代码实现
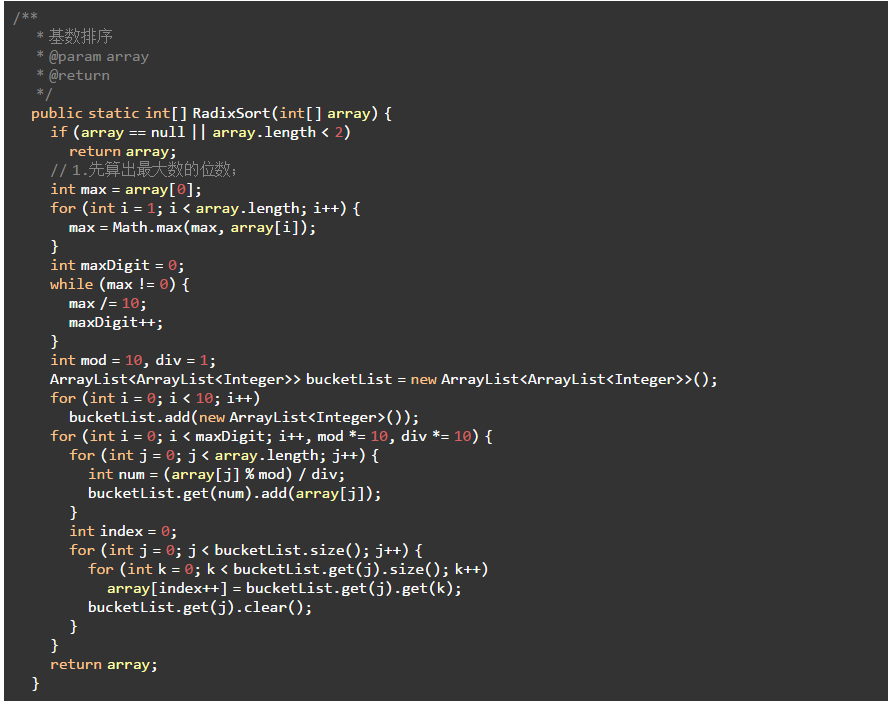