机器学习实战第9章树回归

CART(classificatiion and regression trees)分类回归树

• CART既能用于分类，也能用于回归
• CART是二叉树

CART算法由决策树的生成和决策树的剪枝两步组成。

1 CART生成

1.1回归树

回归树采用平方误差最小化准则，分类树采用基尼指数最小化准则，进行特征选择，生成二叉树。

 　　　　

1.2 分类树

分类树采用基尼指数选择最优特征，同时决定该值的最优二值切分点。

　　

 

     

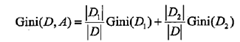
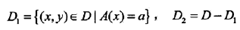
2 CART剪枝

首先从生成算法产生的决策树T₀底端开始不断剪枝，直到T0的根节点，形成一个子树序列{T0,T1,…,Tn}；然后通过交叉验证法在独立的验证数据集上对子树序列进行测试，从中选择最优子树

1.剪枝，形成子树序列

剪枝过程中，计算子树的损失函数：

　　　　

其中T为任意子树，|T|为树T的节点个数，参数a权衡训练数据的拟合程度与模型的复杂度。

可以用递归的方法对树进行剪枝，将a从小增大，a₀<a₁<...<a_n<+无穷，产生一系列的区间[a_i，a_i+1)，i =0,1,...,n；剪枝得到的子树序列对应着区间[a_i，a_i+1)，i =0,1,...,n的最优子树序列{T_0, T_{1, ... ,} Tn}，序列中的子树是嵌套的。

对T₀中每一内部结点t，计算

　　　　　　

3 CART算法实现
3.1 CART算法在回归中的应用

3.1.1构建树

算法：

对每个特征：

　　对特征的每个取值：

　　　　将数据集切分成两部分

　　　　计算切分的误差

　　　　如果当前误差小于当前最小误差，则更新当前最小误差，并更新最佳切分属性和切分值

返回最佳切分的特征和切分值

import numpy as np
from matplotlib import pyplot as plt

def loadDataSet(fileName):
    dataMat = []
    fr = open(fileName)
    for line in fr.readlines():
        curLine = line.strip().split('\t')
        fltLine = map(float, curLine)   #将数据映射成浮点型,返回的是map的地址
        dataMat.append(list(fltLine))
    return dataMat


def plotData(dataMat):
    x = dataMat[:,0].tolist()
    y = dataMat[:,1].tolist()
    plt.scatter(x,y)
    plt.title('DataSet')
    plt.xlabel('x')
    plt.ylabel('y')
    plt.show()


def plotData2(dataMat):
    x = dataMat[:, 1].tolist()
    y = dataMat[:, 2].tolist()
    plt.scatter(x, y)
    plt.title('DataSet')
    plt.xlabel('x')
    plt.ylabel('y')
    plt.show()


def binSplitDataSet(dataSet, feature, value):
    """
     函数说明：根据某个特征及值对数据集进行切分
    :param dataSet: 数据集
    :param feature: 特征
    :param value: 特征值
    :return: 切分后的数据
    """
    mat0 = dataSet[np.nonzero(dataSet[:,feature] > value),:][0]
    mat1 = dataSet[np.nonzero(dataSet[:,feature] <= value),:][0]
    return mat0, mat1


"""
    下面构建回归树
"""
def regLeaf(dataSet):
    """
    函数说明：生成叶节点
    :param dataSet: 数据集
    :return: 使用均值作为叶节点的值
    """
    # print(dataSet)
    return np.mean(dataSet[:,-1])


def regErr(dataSet):
    """
    函数说明：误差估计函数
    :param dataSet: 数据集
    :return: 总方差
    """
    return np.var(dataSet[:-1]) * np.shape(dataSet)[0]


def chooseBestSplit(dataSet, leafType=regLeaf, errType=regErr, ops=(1,4)):
    """
    函数说明：找到数据的最佳二元切分方式函数
    :param dataSet: 数据将
    :param leafType: 生成叶节点
    :param errType: 误差估计函数
    :param ops:用户自定义参数构成的元组
    :return:
        bestIndex :最佳切分特征的下标
        bestValue： 最优切分值
    """
    """
    伪代码：
         首先判断是否所有值相等：
         否：计算误差值，初始化最佳误差，最优切分特征下标，最优切分值
            遍历每个特征：
                遍历特征的每个值：
                    将数据切分为两部分
                    判断是否小于最少切分样本值：
                    是：跳出循环
                    否：计算切分后误差
                        如果切分后误差小于当前最佳误差，则更新最优切分特征下标，最优切分值，最优误差
            如果误差下降值小于最小误差值,则返回最佳切分特征值和最优切分值
    """
    tolS = ops[0];  tolN = ops[1]   #tolS是允许的最小误差下降值,tolN是切分的最少样本
    if len(set(dataSet[:,-1].T.tolist()[0])) == 1: #如果所有值相等则退出，根据set特性
        return None, leafType(dataSet)
    m,n = np.shape(dataSet)
    #the choice of the best feature is driven by Reduction in RSS error from mean
    S = errType(dataSet)    #计算误差值
    bestS = np.inf; bestIndex = 0; bestValue = 0
    for featIndex in range(n-1):    #遍历每个特征值
        for splitVal in set((dataSet[:,featIndex].T.tolist())[0]):  #遍历特征的每个值
            # print(featIndex, splitVal)
            mat0, mat1 = binSplitDataSet(dataSet, featIndex, splitVal)  #将数据集切分为两部分
            if (np.shape(mat0)[0] < tolN) or (np.shape(mat1)[0] < tolN): continue   #如果小于切分的最少样本数则直接跳到下一次循环
            newS = errType(mat0) + errType(mat1)    #计算新的误差
            if newS < bestS: #如果小于最佳误差则更新
                bestIndex = featIndex
                bestValue = splitVal
                bestS = newS
    #如果误差下降值小于允许的最小误差下降值，则不需要切分
    if (S - bestS) < tolS:
        return None, leafType(dataSet) #exit cond 2
    #切分数据集
    mat0, mat1 = binSplitDataSet(dataSet, bestIndex, bestValue)
    #如果切分后的数据集个数小于tolN,则不进行切分
    # if (np.shape(mat0)[0] < tolN) or (np.shape(mat1)[0] < tolN):
    #     return None, leafType(dataSet)
    return bestIndex, bestValue#返回最佳切分特征的下标和最优切分值


def createTree(dataSet, leafType = regLeaf, errType = regErr, ops=(1,4)):
    """
    函数说明：建树
    :param dataSet: 数据集
    :param leafType: 生成叶子节点函数
    :param errType: 误差函数
    :param ops: 用户自定义参数，对树进行预剪枝
    :return: 树
    """
    feat, val = chooseBestSplit(dataSet, leafType, errType, ops)
    if feat == None: return val
    retTree = {}
    retTree['spInd'] = feat
    retTree['spVal'] = val
    lSet, rSet = binSplitDataSet(dataSet, feat, val)
    retTree['left'] = createTree(lSet, leafType, errType, ops)
    retTree['right'] = createTree(rSet, leafType, errType, ops)
    return retTree

if __name__ == '__main__':

    ex00Data = loadDataSet('txt/ex00.txt')
    ex00Mat = np.mat(ex00Data)
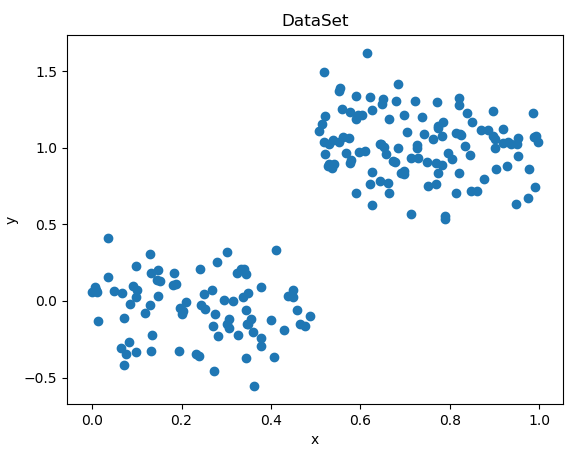
    plotData(ex00Mat)
    myTree1 = createTree(ex00Mat)
    print(myTree1)

    ex0Data = loadDataSet('txt/ex0.txt')
    ex0Mat = np.mat(ex0Data)
    plotData2(ex0Mat)
    myTree2 = createTree(ex0Mat)
    print(myTree2)
    print(createTree(ex0Mat, ops=(0,1)))　　#tolS为0，tolN为1

生成结果如下：　　

     

       

 3.1.2 树剪枝

 为了防止过拟合，需要对树进行剪枝

（1）预剪枝

if __name__ == '__main__':
    ex2Data = loadDataSet('txt/ex2.txt')
    ex2Mat = np.mat(ex2Data)
    plotData(ex2Mat)
    ex2Tree = createTree(ex2Mat)
    print(ex2Tree)   #非常多的叶子节点
    print(createTree(ex2Mat,ops=(10000,4))) #只有两个叶子节点，tolS对误差的数据集非常敏感

在生成树的过程中进行剪枝，如前面设置的最低下降误差值tolS和最小节点数tolN

使用ex2.txt来构建树，ex2.txt的数量级是ex0.txt的100倍

可以看出停止条件tolS对误差的数量级十分敏感。

 （2）后剪枝

 使用后剪枝需要将数据集分成测试集和训练集。

剪枝函数的伪代码：

代码如下：

import numpy as np
from matplotlib import pyplot as plt

def loadDataSet(fileName):
    dataMat = []
    fr = open(fileName)
    for line in fr.readlines():
        curLine = line.strip().split('\t')
        fltLine = map(float, curLine)   #将数据映射成浮点型,返回的是map的地址
        dataMat.append(list(fltLine))
    return dataMat


def plotData(dataMat):
    x = dataMat[:,0].tolist()
    y = dataMat[:,1].tolist()
    plt.scatter(x,y)
    plt.title('DataSet')
    plt.xlabel('x')
    plt.ylabel('y')
    plt.show()


def plotData2(dataMat):
    x = dataMat[:, 1].tolist()
    y = dataMat[:, 2].tolist()
    plt.scatter(x, y)
    plt.title('DataSet')
    plt.xlabel('x')
    plt.ylabel('y')
    plt.show()


def binSplitDataSet(dataSet, feature, value):
    """
     函数说明：根据某个特征及值对数据集进行切分
    :param dataSet: 数据集
    :param feature: 特征
    :param value: 特征值
    :return: 切分后的数据
    """
    mat0 = dataSet[np.nonzero(dataSet[:,feature] > value),:][0]
    mat1 = dataSet[np.nonzero(dataSet[:,feature] <= value),:][0]
    return mat0, mat1


"""
    下面构建回归树
"""
def regLeaf(dataSet):
    """
    函数说明：生成叶节点
    :param dataSet: 数据集
    :return: 使用均值作为叶节点的值
    """
    # print(dataSet)
    return np.mean(dataSet[:,-1])


def regErr(dataSet):
    """
    函数说明：误差估计函数
    :param dataSet: 数据集
    :return: 总方差
    """
    return np.var(dataSet[:-1]) * np.shape(dataSet)[0]


def chooseBestSplit(dataSet, leafType=regLeaf, errType=regErr, ops=(1,4)):
    """
    函数说明：找到数据的最佳二元切分方式函数
    :param dataSet: 数据将
    :param leafType: 生成叶节点
    :param errType: 误差估计函数
    :param ops:用户自定义参数构成的元组
    :return:
        bestIndex :最佳切分特征的下标
        bestValue： 最优切分值
    """
    """
    伪代码：
         首先判断是否所有值相等：
         否：计算误差值，初始化最佳误差，最优切分特征下标，最优切分值
            遍历每个特征：
                遍历特征的每个值：
                    将数据切分为两部分
                    判断是否小于最少切分样本值：
                    是：跳出循环
                    否：计算切分后误差
                        如果切分后误差小于当前最佳误差，则更新最优切分特征下标，最优切分值，最优误差
            如果误差下降值小于最小误差值,则返回最佳切分特征值和最优切分值
    """
    tolS = ops[0];  tolN = ops[1]   #tolS是允许的最小误差下降值,tolN是切分的最少样本
    if len(set(dataSet[:,-1].T.tolist()[0])) == 1: #如果所有值相等则退出，根据set特性
        return None, leafType(dataSet)
    m,n = np.shape(dataSet)
    #the choice of the best feature is driven by Reduction in RSS error from mean
    S = errType(dataSet)    #计算误差值
    bestS = np.inf; bestIndex = 0; bestValue = 0
    for featIndex in range(n-1):    #遍历每个特征值
        for splitVal in set((dataSet[:,featIndex].T.tolist())[0]):  #遍历特征的每个值
            # print(featIndex, splitVal)
            mat0, mat1 = binSplitDataSet(dataSet, featIndex, splitVal)  #将数据集切分为两部分
            if (np.shape(mat0)[0] < tolN) or (np.shape(mat1)[0] < tolN): continue   #如果小于切分的最少样本数则直接跳到下一次循环
            newS = errType(mat0) + errType(mat1)    #计算新的误差
            if newS < bestS: #如果小于最佳误差则更新
                bestIndex = featIndex
                bestValue = splitVal
                bestS = newS
    #如果误差下降值小于允许的最小误差下降值，则不需要切分
    if (S - bestS) < tolS:
        return None, leafType(dataSet) #exit cond 2
    #切分数据集
    mat0, mat1 = binSplitDataSet(dataSet, bestIndex, bestValue)
    #如果切分后的数据集个数小于tolN,则不进行切分
    # if (np.shape(mat0)[0] < tolN) or (np.shape(mat1)[0] < tolN):
    #     return None, leafType(dataSet)
    return bestIndex, bestValue#返回最佳切分特征的下标和最优切分值


def createTree(dataSet, leafType = regLeaf, errType = regErr, ops=(1,4)):
    """
    函数说明：建树
    :param dataSet: 数据集
    :param leafType: 生成叶子节点函数
    :param errType: 误差函数
    :param ops: 用户自定义参数，对树进行预剪枝
    :return: 树
    """
    feat, val = chooseBestSplit(dataSet, leafType, errType, ops)
    if feat == None: return val
    retTree = {}
    retTree['spInd'] = feat
    retTree['spVal'] = val
    lSet, rSet = binSplitDataSet(dataSet, feat, val)
    retTree['left'] = createTree(lSet, leafType, errType, ops)
    retTree['right'] = createTree(rSet, leafType, errType, ops)
    return retTree


def isTree(obj):
    """
    函数说明：判断是否是一棵树
    :param obj:
    :return:
    """
    return (type(obj).__name__=='dict')


def getMean(tree):
    """
    函数说明：递归函数，对树进行塌陷处理（返回树平均值）
    :param tree: 树
    :return: 树的左右子树的均值
    """
    if isTree(tree['left']): tree['left'] = getMean(tree['left'])
    if isTree(tree['right']): tree['right'] = getMean(tree['right'])
    return (tree['left'] + tree['right']) / 2.0


def prnue(tree, testData):
    """
    函数说明：后剪枝函数，使用测试数据对树进行剪枝
    :param tree:  待剪枝的树
    :param testData:   测试数据
    :return: 剪枝后的树
    """
    """
        树的后剪枝：
        伪代码:
            基于已有的树切分测试数据：
                如果存在任一子集是一棵树，则在该子集递归剪枝过程
                计算将当前两个叶节点合并后的误差
                计算没有合并时的误差
                如果合并可以降低误差则进行合并
    """
    #如果测试数据集为空，进行塌陷处理
    if(np.shape(testData[0]) == 0): return getMean(tree)
    # if isTree(tree['left']) and isTree(tree['right']):
    lSet, rSet = binSplitDataSet(testData, tree['spInd'], tree['spVal'])
    if isTree(tree['left']): tree['left'] = prnue(tree['left'], lSet)  #左子集不是单个节点，则对左子树进行剪枝
    if isTree(tree['right']): tree['right'] = prnue(tree['right'], rSet) #右子集不是单个节点，则对右子树进行剪枝
    if not isTree(tree['left']) and not isTree(tree['right']):  #左右子集都是单个节点
        errNoMerge = sum(np.power((lSet[:,-1] - tree['left']),2)) + sum(np.power((rSet[:,-1] - tree['right']),2)) #未合并的误差
        treeMean = getMean(tree)
        errMerge = sum(np.power(testData[:,-1] - treeMean, 2))   #合并后误差
        print(errNoMerge, errMerge)
        if errMerge < errNoMerge:   #如果合并后误差小于合并前误差则合并
            print("merging")
            return treeMean
        else: return tree
    else: return tree

if __name__ == '__main__':
    ex2Data = loadDataSet('txt/ex2.txt')
    ex2Mat = np.mat(ex2Data)
    plotData(ex2Mat)
    ex2Tree = createTree(ex2Mat)
    print(ex2Tree) 

    ex2TestData = loadDataSet('txt/ex2test.txt')
    prnueTree = prnue(ex2Tree, np.mat(ex2TestData))　　#对ex2Tree进行剪枝
    print(prnueTree)

 3.2 模型树

模型树的节点是线性回归函数

模型树的代码：

def loadDataSet(fileName):
    dataMat = []
    fr = open(fileName)
    for line in fr.readlines():
        curLine = line.strip().split('\t')
        fltLine = map(float, curLine)   #将数据映射成浮点型,返回的是map的地址
        dataMat.append(list(fltLine))
    return dataMat

def binSplitDataSet(dataSet, feature, value):
    """
     函数说明：根据某个特征及值对数据集进行切分
    :param dataSet: 数据集
    :param feature: 特征
    :param value: 特征值
    :return: 切分后的数据
    """
    mat0 = dataSet[np.nonzero(dataSet[:,feature] > value),:][0]
    mat1 = dataSet[np.nonzero(dataSet[:,feature] <= value),:][0]
    return mat0, mat1


def linearSolve(dataSet):
    """
    函数说明：生成数据集的线性模型
    :param dataSet: 数据集
    :return: 系数,X,Y
    """
    m, n = np.shape(dataSet)
    X = np.mat(np.ones((m, n))); Y = np.mat(np.zeros((m, 1)))
    X[:,1:n] = dataSet[:,0:n-1]
    Y = dataSet[:,-1]
    xTx = X.T * X
    # linalg.det()计算行列式，若为0，则不可逆
    if np.linalg.det(xTx) == 0.0:
        print("This matrix is singular, cannot do inverse")
        return
    # 回归系数ws = (X^TX)^-1X^Ty
    ws = xTx.I * (X.T * Y)
    return ws, X, Y


def modelLeaf(dataSet):
    """
    函数说明：线性模型树的叶节点生成函数
    :param dataSet:
    :return:
    """
    ws, X, Y = linearSolve(dataSet)
    return ws


def modelErr(dataSet):
    """
    函数说明：线性模型误差计算函数
    :param dataSet: 数据集
    :return: 误差
    """
    ws, X, Y = linearSolve(dataSet)
    yHat = X * ws
    return sum(np.power((Y - yHat), 2))

def chooseBestSplit(dataSet, leafType=regLeaf, errType=regErr, ops=(1,4)):
    """
    函数说明：找到数据的最佳二元切分方式函数
    :param dataSet: 数据将
    :param leafType: 生成叶节点
    :param errType: 误差估计函数
    :param ops:用户自定义参数构成的元组
    :return:
        bestIndex :最佳切分特征的下标
        bestValue： 最优切分值
    """
    """
    伪代码：
         首先判断是否所有值相等：
         否：计算误差值，初始化最佳误差，最优切分特征下标，最优切分值
            遍历每个特征：
                遍历特征的每个值：
                    将数据切分为两部分
                    判断是否小于最少切分样本值：
                    是：跳出循环
                    否：计算切分后误差
                        如果切分后误差小于当前最佳误差，则更新最优切分特征下标，最优切分值，最优误差
            如果误差下降值小于最小误差值,则返回最佳切分特征值和最优切分值
    """
    tolS = ops[0];  tolN = ops[1]   #tolS是允许的最小误差下降值,tolN是切分的最少样本
    if len(set(dataSet[:,-1].T.tolist()[0])) == 1: #如果所有值相等则退出，根据set特性
        return None, leafType(dataSet)
    m,n = np.shape(dataSet)
    #the choice of the best feature is driven by Reduction in RSS error from mean
    S = errType(dataSet)    #计算误差值
    bestS = np.inf; bestIndex = 0; bestValue = 0
    for featIndex in range(n-1):    #遍历每个特征值
        for splitVal in set((dataSet[:,featIndex].T.tolist())[0]):  #遍历特征的每个值
            # print(featIndex, splitVal)
            mat0, mat1 = binSplitDataSet(dataSet, featIndex, splitVal)  #将数据集切分为两部分
            if (np.shape(mat0)[0] < tolN) or (np.shape(mat1)[0] < tolN): continue   #如果小于切分的最少样本数则直接跳到下一次循环
            newS = errType(mat0) + errType(mat1)    #计算新的误差
            if newS < bestS: #如果小于最佳误差则更新
                bestIndex = featIndex
                bestValue = splitVal
                bestS = newS
    #如果误差下降值小于允许的最小误差下降值，则不需要切分
    if (S - bestS) < tolS:
        return None, leafType(dataSet) #exit cond 2
    #切分数据集
    mat0, mat1 = binSplitDataSet(dataSet, bestIndex, bestValue)
    #如果切分后的数据集个数小于tolN,则不进行切分
    # if (np.shape(mat0)[0] < tolN) or (np.shape(mat1)[0] < tolN):
    #     return None, leafType(dataSet)
    return bestIndex, bestValue#返回最佳切分特征的下标和最优切分值

　　
　def createTree(dataSet, leafType = regLeaf, errType = regErr, ops=(1,4)):
    """
    函数说明：建树
    :param dataSet: 数据集
    :param leafType: 生成叶子节点函数
    :param errType: 误差函数
    :param ops: 用户自定义参数，对树进行预剪枝
    :return: 树
    """
    feat, val = chooseBestSplit(dataSet, leafType, errType, ops)
    if feat == None: return val
    retTree = {}
    retTree['spInd'] = feat
    retTree['spVal'] = val
    lSet, rSet = binSplitDataSet(dataSet, feat, val)
    retTree['left'] = createTree(lSet, leafType, errType, ops)
    retTree['right'] = createTree(rSet, leafType, errType, ops)
    return retTree

if __name__ == '__main__':
    exp2Data = loadDataSet('txt/exp2.txt')
    exp2Mat = np.mat(exp2Data)
    exp2Tree = createTree(exp2Mat, modelLeaf, modelErr, (1,10)) #模型树
     print(exp2Tree)

3.3 进行预测——简单线性回归 回归树 模型树的对比

使用决定系数R^2值来判断预测效果，越接近于1越好

#!/usr/bin/env python
# encoding: utf-8
'''
@author: shuhan Wei 
@software: pycharm
@file: treeFore.py
@time: 18-9-13 下午6:33
@desc:树回归预测
'''
import regTrees
import numpy as np


def regTreeEval(model, inDat):
    """
    函数说明：回归树的单个节点预测值
    :param model: 某一节点的值
    :param inDat: 空值
    :return: 预测的浮点数
    """
    return float(model)


def modelTreeEval(model, inDat):
    """
    函数说明：模型树的预测值
    :param model: 预测节点的回归系数
    :param inDat: 某个测试数据
    :return: 预测值
    """
    n = np.shape(inDat)[1]
    X = np.mat(np.ones((1, n + 1)))
    X[:, 1:n + 1] = inDat
    return float(X * model)


def treeForeCast(tree, inData, modelEval=regTreeEval):
    if not regTrees.isTree(tree): return modelEval(tree, inData)
    if inData[tree['spInd'],0] > tree['spVal']:
        if regTrees.isTree(tree['left']):
            return treeForeCast(tree['left'], inData, modelEval)
        else:
            return modelEval(tree['left'], inData)
    else:
        if regTrees.isTree(tree['right']):
            return treeForeCast(tree['right'], inData, modelEval)
        else:
            return modelEval(tree['right'], inData)


def createForeCast(tree, testData, modelEval=regTreeEval):
    m = len(testData)
    yHat = np.mat(np.zeros((m, 1)))
    for i in range(m):
        yHat[i, 0] = treeForeCast(tree, np.mat(testData[i]), modelEval)
    return yHat


if __name__ == '__main__':
    trainMat = np.mat(regTrees.loadDataSet('txt/bikeSpeedVsIq_train.txt'))
    testMat = np.mat(regTrees.loadDataSet('txt/bikeSpeedVsIq_test.txt'))
    regTrees.plotData(trainMat)
    # 使用回归树模型进行预测
    regTree = regTrees.createTree(trainMat, ops=(1,20))
    yHat = createForeCast(regTree, testMat, regTreeEval)
    #计算R^2值,越接近于1越好
    cor1 = np.corrcoef(yHat, testMat[:, 1], rowvar=0)[0,1]
    print(cor1)

    #使用模型树进行预测
    modelTree = regTrees.createTree(trainMat, regTrees.modelLeaf, regTrees.modelErr, (1,20))
    yHat = createForeCast(modelTree, testMat[:, 0], modelTreeEval)
    col2 = np.corrcoef(yHat, testMat[:, 1], rowvar=0)[0, 1]
    print(col2)

　　#使用简单线性模型
　　ws, X, Y = regTrees.linearSolve(trainMat)
　　for i in range(np.shape(testMat)[0]):
   　　yHat[i] = testMat[i, 0] * ws[1, 0] + ws[0, 0]
　　col3 = np.corrcoef(yHat, testMat[:, 1], rowvar=0)[0, 1]
　　print(col3)

　　　　

　　　　　　

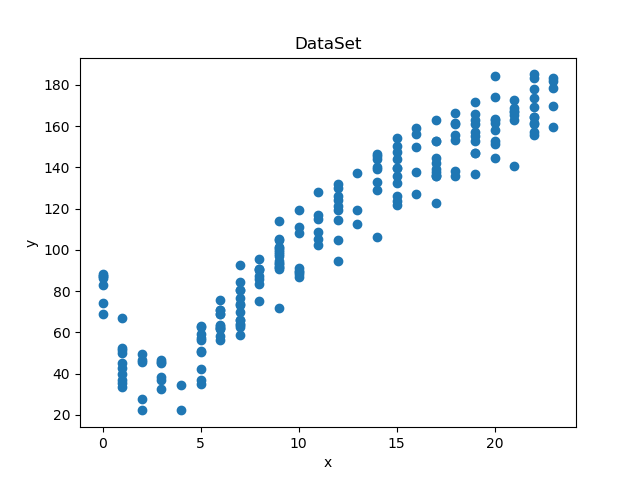
　　　　可以看到数据集的分布像两段线性函数，从R^2值可以看出模型树的预测效果最好。