将不同的分类器组合起来,这种组合结果被称为集成方法或元算法(meta-algorithm)。
使用集成方法时会有多种形式:(1)可以是不同算法的集成(2)可以是同一种算法在不同设置下的集成(3)数据集不同部分分配给不同分类器之后的集成,等等
接下来介绍基于同一种分类器多个不同实例的两种不同计算方法bagging和boosting
1. bagging
原理:从原始数据集选择S次后得到S个新数据集的一种技术。新数据集和原数据集的大小相等。每个数据集都是通过在原始数据集中随机选择一个样本来进行替换而得到的。这里的替换就意味着可以多次地选择同一样本,允许重复。(取出,放回)。将某个学习算法分别作用于每个数据集就得到S个分类器。每个分类器的权值相同
2. boosting
原理:集中关注被已有分类器错分的那些数据来获得新的分类器。是所有分类器加权求和结果,每个分类器的权值不同。
从弱学习算法出发,反复学习,得到一系列弱分类器(又称为基本分类器),然后组合这些弱分类器,构成一个强分类器。大多的boosting方法都是改变训练数据的概率分布(训练数据的权值分布),针对不同的训练数据分布调用弱学习算法学习一系列弱分类器。
那么对于boosting方法,有两个问题需要回答:(1) 在每一轮如何改变训练数据的权值或者概率分布?
(2)如何将弱分类器组合成一个强分类器?
接下来介绍boosting中一个最流行的算法AdaBoost,在AdaBoost是如何解决上面两个问题的呢?对于第一个问题,AdaBoost的做法是,提高那些被前一轮弱分类器错误分类样本的权值,而降低被正确分类样本的权值。对于第二个问题,AdaBoost采取加权多数表决的方法,加大分类误差率小的弱分类器的权值,减小分类误差率大的弱分类器的权值
3. AdaBoost算法
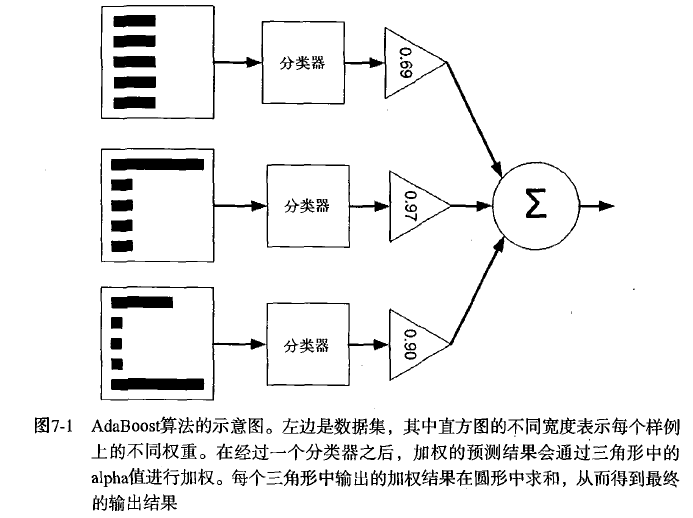
下面是具体的算法:


对于(2)中的(d)根据下式得到
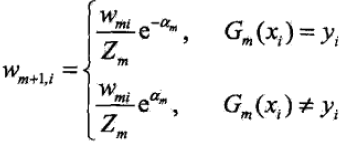
具体代码如下:
import numpy as np from math import log def loadSimpData(): datMat = np.matrix([ [1. , 2.1], [2, 1.1], [1.3, 1.], [1., 1.], [2., 1.] ]) classLabels = [1.0, 1.0, -1.0, -1.0, 1.0] return datMat, classLabels def loadDataSet(fileName): #general function to parse tab -delimited floats numFeat = len(open(fileName).readline().split('\t')) #get number of fields dataMat = []; labelMat = [] fr = open(fileName) for line in fr.readlines(): lineArr =[] curLine = line.strip().split('\t') for i in range(numFeat-1): lineArr.append(float(curLine[i])) dataMat.append(lineArr) labelMat.append(float(curLine[-1])) return dataMat,labelMat """ 函数说明:通过阈值比较对数据进行分类 Parameters: dataMatrix -输入数据 dimen -第几列 threshVal -阈值 threshIneq -不等号 return: 分类结果 """ def stumpClassify(dataMatrix, dimen, threshVal, threshIneq): retArray = np.ones((np.shape(dataMatrix)[0],1)) if threshIneq == 'lt': retArray[dataMatrix[:,dimen] <= threshVal] = -1.0 else: retArray[dataMatrix[:,dimen] <= threshVal] = 1.0 return retArray """ 函数说明:建立单层决策树 Parameters: dataArr -输入数据集 classLabels -分类 D -权重向量 return: bestStump -最佳单层决策树字典 minError -最小错误率 bestClassEst -最佳类别估计值 """ def buildStump(dataArr, classLabels, D): dataMatrix = np.mat(dataArr) labelMat = np.mat(classLabels).T m, n = np.shape(dataMatrix) #numSteps:步数; bestStump:保存最佳单层决策树的相关信息; bestClassEst:最佳预测结果 numSteps = 10.0; bestStump = {}; bestClassEst = np.mat(np.zeros((m, 1))) minError = np.inf # 对每个特征进行遍历 for i in range(n): rangeMin = dataMatrix[:,i].min(); rangeMax = dataMatrix[:,i].max(); stepSize = (rangeMax - rangeMin) / numSteps # 遍历所有步长,阈值设置为整个取值范围之外也可以 for j in range(-1, int(numSteps)+1): # 在大于和小于之间切换 for inequal in ['lt', 'gt']: threshVal = (rangeMin + float(j) * stepSize) predictedVals = stumpClassify(dataMatrix, i, threshVal, inequal) errArr = np.mat(np.ones((m, 1))) errArr[predictedVals == labelMat] = 0 weightError = D.T * errArr #计算加权错误率 print("split:dim %d,thresh %.2f,thresh inequal: %s,the weighted error is %.3f"%(i,threshVal,inequal,weightError)) # 找到最小错误率的最佳单层决策树,并保存相关信息 if weightError < minError: minError = weightError bestClassEst = predictedVals.copy() bestStump['dim'] = i bestStump['thresh'] = threshVal bestStump['ineq'] = inequal return bestStump, minError, bestClassEst """ 函数说明:基于单层决策树的AdaBoost训练过程 Patameters: dataArr -数据集 classLabels -数据标签 numIt -迭代次数 return: weakClassArr -所有的最佳分类器决策树 aggClassEst -累计分类估计 """ def adaBoostTrainDS(dataArr,classLabels,numIt=40): weakClassArr = [] m = np.shape(dataArr)[0] D = np.mat(np.ones((m,1))/m) #init D to all equal aggClassEst = np.mat(np.zeros((m,1))) for i in range(numIt): bestStump,error,classEst = buildStump(dataArr,classLabels,D)#build Stump print("D:",D.T) # alpha公式:alpha=1/2*ln((1-error)/error) # max(error, 1e-16)是为了防止error=0的情况 alpha = float(0.5 * log((1.0 - error) / max(error, 1e-16))) bestStump['alpha'] = alpha weakClassArr.append(bestStump) #保存最优单层决策树 print("classEst: ",classEst.T) #更新D,D是一个概率分布向量,总和为1 # D=(D*exp(-alpha*classLabels*classEst))/D.sum() # classEst是分类器预测的分类结果,classEst是 # np.multiply是矩阵对应元素相乘,返回和矩阵大小一样,classLabels是m*1,classEst是1*m expon = np.multiply(-1 * alpha * np.mat(classLabels).T,classEst) #exponent for D calc, getting messy D = np.multiply(D, np.exp(expon)) #Calc New D for next iteration D = D / D.sum() #更新累计估计类别 #aggClassEst记录每个类别的累计估计值,最终分类函数为f(x) = sign(aggClassEst) aggClassEst += alpha*classEst print("aggClassEst: ",aggClassEst.T) #计算错误率 aggErrors = np.multiply(np.sign(aggClassEst) != np.mat(classLabels).T,np.ones((m,1))) errorRate = aggErrors.sum() / m print("total error: ",errorRate) #误差为0时退出循环 if errorRate == 0.0: break return weakClassArr,aggClassEst
""" 函数说明:测试算法,AdaBoost分类函数 Parameters: datToClass -待分类样例 classifierArr -多个弱分类器组成的数组 return: 类别 """ def adaClassify(datToClass,classifierArr): dataMatrix = np.mat(datToClass) m = np.shape(dataMatrix)[0] aggClassEst = np.mat(np.zeros((m,1))) for i in range(len(classifierArr)): #基于每个分类器得到一个类别值 print(classifierArr[i]) classEst = stumpClassify(dataMatrix,classifierArr[i]['dim'],\ classifierArr[i]['thresh'],\ classifierArr[i]['ineq'])#call stump classify aggClassEst += classifierArr[i]['alpha']*classEst print(aggClassEst) return np.sign(aggClassEst)
if __name__ == '__main__': datMat, classLabels = loadSimpData() D = np.mat(np.ones((5,1)) / 5) buildStump(datMat, classLabels, D) classifierArr, aggClassEst = adaBoostTrainDS(datMat, classLabels) print(adaClassify([0,0],classifierArr)) print(adaClassify([[0,0],[1,0],[2,2]],classifierArr)) #将第5章的马疝病数据应用到AdaBoost算法中 datArr, labelArr = loadDataSet('horseColicTraining2.txt') classifierArr,aggClassEst = adaBoostTrainDS(datArr, labelArr, 10) testArr, testLableArr = loadDataSet('horseColicTest2.txt') prediction = adaClassify(testArr, classifierArr) errArr = np.mat(np.ones((67,1))) errRate = errArr[prediction!= np.mat(testLableArr).T].sum() / 67 print(errRate)
4. 非均衡分类问题
非均衡分类问题是指,在很多情况下不同类别的分类代价并不相等。例如对于垃圾邮件过滤的例子,如果我们把所有的邮件都预测为垃圾邮件,则用户可能会错过重要的合法邮件,如果我们把所有的邮件都预测为合法邮件,则会影响到用户体验,但是这两种代价是不一样的。
性能度量
性能度量是指衡量模型泛化能力的评价标准。在回归问题中常用的性能度量是“均方误差”(mean squared error)。而在分类问题中错误率是一种常用的性能度量,错误率是指分类错误的样本占样本总数的比例,实际上这样的度量错误掩盖了样例如何被错分的事实。在机器学习中,有一个普遍使用的称为混淆矩阵的工具,它可以帮助人们更好的了解分类中的错误。
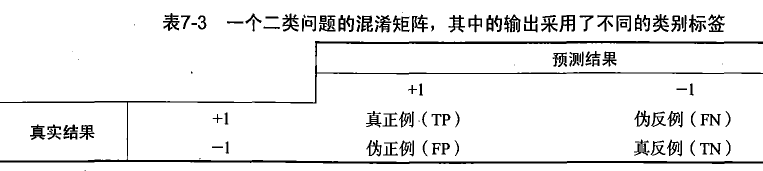
正确率/查准率(precision):预测为正例的样本中真正正例的比例
![]()
召回率/查全率(recall):预测为正例的真正例占所有正例的比例
![]()
通常查准率和查全率是一对矛盾的度量。一般来说查准率高的时候,查全率会偏低;而查全率高的时候,查准率会偏低。通常只有在一些简单任务中查准率和查全率都很高。
P-R图能直观的显示出学习器在样本总体上的查全率、查准率。

图中的平衡点(BEP)是查准率=查全率时的取值,BEP高则更优,对于图中的三个学习器,A优于B优于C。
但BEP还是过于简化了,通常使用的是F1度量:

对于有偏好的情况:
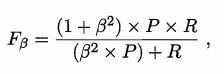
其中ß>O 度量了查全率对查准率的相对重要性. ß = 1时退化为标准的F1; ß> 1 时查全率有更大影响; ß < 1 时查准率有更大影响
接下来介绍ROC曲线
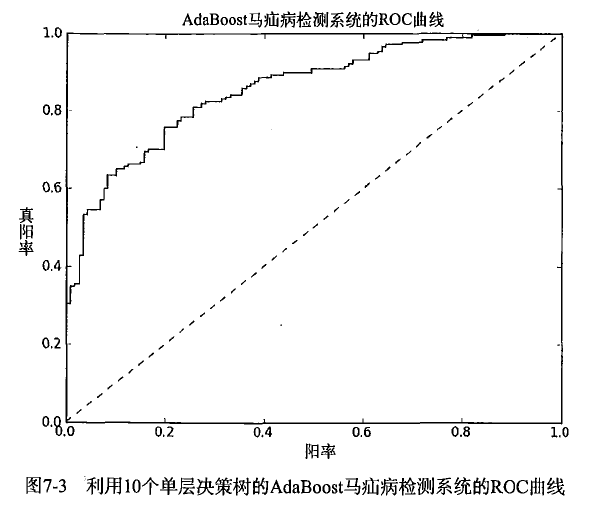
纵坐标为真阳率(真正例率):
![]()
横坐标为假阳率(假正例率):
![]()
AUC(area under the curve):ROC曲线下的面积,对不同的ROC曲线进行比较的一个指标,给出的是分类器的平均性能值。一个完美的分类器的AUC是1,而随机猜测的AUC则为0.5。若一个学习器的ROC曲线能把另一个学习器的ROC曲线完全包住,则这个学习器的性能比较好。
实现代码如下,书中是以(1.0,1.0)点为起点来画曲线的,我改成了以(0.0,0.0)为起点,这样更好理解一些。
绘制过程:给定m+个正例,m-个反例,将分类器的预测强度进行排序,然后把分类阈值设为最大,即把所有的样例都预测为反例,此时真阳率和假阳率均为0,在坐标(0,0)处标记一个点。然后将分类阈值依次设置为每个样例的预测值,即依次将每个样例划分为正例。设前一个坐标点为(x,y),若当前点为真正例,则它的坐标为(x,y+1/m+),真阳率变大;若当前点为假正例,则坐(x+1/m-,y),假阳率变大。
""" 函数说明:ROC曲线绘制及AUC计算函数 Parameters: predStrengths -分类器的预测强度,马疝病数据集中为1*299 classLabels -分类标签 """ def plotROC(predStrengths, classLabels): import matplotlib.pyplot as plt # cur = (1.0,1.0) #绘制光标的位置 cur = (0.0,0.0) #绘制光标的位置 ySum = 0.0 #用于计算AUC的值 numPosClas = sum(np.array(classLabels)==1.0) #保存正例的数目 yStep = 1/float(numPosClas); xStep = 1/float(len(classLabels)-numPosClas) #y轴的步长、x轴的步长 sortedIndicies = predStrengths.argsort()#获取排好序的索引,从小到大 fig = plt.figure() fig.clf() ax = plt.subplot(111) #loop through all the values, drawing a line segment at each point for index in sortedIndicies.tolist()[0][::-1]: #改为从大到小 if classLabels[index] == 1.0: #标签为1修改真阳率 delX = 0; delY = yStep; else: #标签不为1,修改假阳率 delX = xStep; delY = 0; ySum += cur[1] #保存纵坐标为之后计算面积 #draw line from cur to (cur[0]-delX,cur[1]-delY) # ax.plot([cur[0],cur[0]-delX],[cur[1],cur[1]-delY], c='b') ax.plot([cur[0],cur[0]+delX],[cur[1],cur[1]+delY], c='b') # cur = (cur[0]-delX,cur[1]-delY) cur = (cur[0]+delX,cur[1]+delY) ax.plot([0,1],[0,1],'b--') plt.xlabel('False positive rate'); plt.ylabel('True positive rate') plt.title('ROC curve for AdaBoost horse colic detection system') ax.axis([0,1,0,1]) plt.show() print("the Area Under the Curve is: ",ySum*xStep) #AUC,小矩形面积之和 if __name__ == '__main__': datArr, labelArr = loadDataSet('horseColicTraining2.txt') classifierArr,aggClassEst = adaBoostTrainDS(datArr, labelArr, 50) #testArr, testLableArr = loadDataSet('horseColicTest2.txt') #prediction = adaClassify(testArr, classifierArr) #errArr = np.mat(np.ones((67,1))) #errRate = errArr[prediction!= np.mat(testLableArr).T].sum() / 67 #print(errRate) plotROC(aggClassEst.T, labelArr)
结果如下:
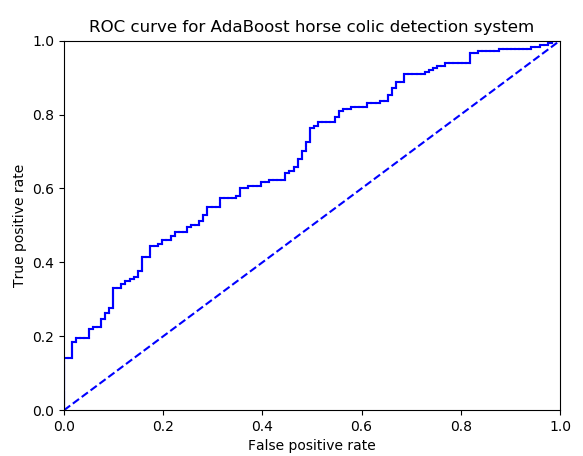
参考:
《机器学习实战》
《机器学习》周志华
《统计学习方法》