地址:http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemCode=3965
题目:
iven two depth-first-search (DFS) sequences of a binary tree, can you find a binary tree which satisfies both of the DFS sequences?
Recall that a binary tree is a tree in which each vertex has at most two children, and the depth-first search is a tree traversing method which starts at the root and explores as far as possible along each branch before backtracking.
Input
There are multiple test cases. The first line of input contains an integer T, indicating the number of test cases. For each test case:
The first line contains an integer n (1 ≤ n ≤ 105), indicating the number of vertices in the binary tree.
The second line contains n integers a1, a2, ..., an (1 ≤ ai ≤ n, ∀ 1 ≤ i < j ≤ n, ai ≠ aj), indicating the first DFS sequence of the binary tree.
The third line of each test case contains n integers b1, b2, ..., bn (1 ≤ bi ≤ n, ∀ 1 ≤ i < j ≤ n, bi ≠ bj), indicating the second DFS sequence of the binary tree.
It is guaranteed that the sum of n over all test cases does not exceed 106, and there always exists at least one possible binary tree.
We kindly remind you that this problem contains large I/O file, so it's recommended to use a faster I/O method. For example, you can use scanf/printf instead of cin/cout in C++.
Output
For each test case, output one line which contains n integers seperated by one space. The i-th integer indicates the father of the i-th vertex in the binary tree which satisfies both of the DFS sequence. If the i-th vertex is the root of the binary tree, output 0 as its father. If there are multiple valid answers, you can output any of them.
Please, DO NOT print extra spaces at the end of each line, or your program may get a "wrong answer" verdict as this problem is special judged.
Sample Input
2
6
3 4 2 5 1 6
3 4 5 2 1 6
3
1 2 3
1 2 3
Sample Output
3 4 0 3 4 1 0 1 2
思路:

通过上图(第一个dfs序列记为a,第二个记为b)
可以看出对于一个没有兄弟节点的节点x,他必然是紧跟在x的父亲节点f的后面。
对于一个有兄弟节点的节点x(兄弟节点记为y),节点x或y必然紧跟在父亲节点f的后面。
所以可以得出结论:通过对比父亲节点后面第一个点是否相同,我们可以判断这父亲节点有几个儿子节点。
如果父亲节点f有两个子节点,但在ab数列中都是先访问左儿子,后访问右儿子,这时似乎结论错了,通过结论只能判断出只有一个子节点。
但这时可以把右儿子当左儿子的子孙节点的儿子节点,这时构造出的树依旧符合两个dfs序列。
这时怎么判断是知道了,但是怎么确定父亲节点呢?
对于在数列ab中f的下一个位置的数相同,则f有一个儿子,那么在数列ab中f的下一个位置就是下一个父亲节点。
如果在数列ab中f的下一个位置的数不同,则f有两个儿子x,y,把x,y当做下一个父亲节点进行递归就好了。
那怎么确定x和y在ab数列中的位置呢?哈希一下即可。
现在可以通过函数solve(int x,int y,int fa),进行递归判断fa后面的节点a[x],b[y]是否相同来确定fa的子节点个数。
void solve(int x,int y,int fa)
{
ans[a[x]]=ans[b[y]]=fa;
if(x>=n||y>=n)return ;
if(a[x]==b[y])
solve(x+1,y+1,a[x]);
else
{
solve(x+1,hb[a[x]]+1,a[x]);//hb是哈希x在b中位置
solve(ha[b[y]]+1,y+1,b[y]);//ha同理
}
}
但是如果有如下数列:
ab.....c......xxxxxx
ac.....b......xxxxxx
上面的代码会出现问题,其递归过程是
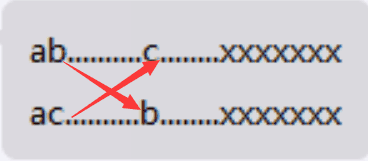
这时从第一数列递归访问完区间bc内的数后,本应该直接return,但代码却还是会继续访问
所以函数还需要加入一个参数,访问的最远距离,可以sz代表第一个数列中能访问到的最远位置。
并且当a[x]!=b[y]时还应递归访问xxxxx。
最终代码如下:
1 void solve(int x,int y,int fa,int sz)
2 {
3 if(x>sz)return;
4 ans[a[x]]=ans[b[y]]=fa;
5 if(a[x]==b[y]) sum[fa]+=1;
6 else sum[fa]+=2;
7 if(x==sz)return;
8 if(a[x]==b[y])
9 solve(x+1,y+1,a[x],sz);
10 else
11 {
12 int ta,tb;
13 ta=ha[b[y]]-1,tb=hb[a[x]]-y+ta;
14 if(x!=ta)
15 solve(x+1,hb[a[x]]+1,a[x],ta);
16 if(y!=hb[a[x]]-1)
17 solve(ta+2,y+1,b[y],tb);
18 if(tb!=sz)
19 solve(tb+1,tb+1-x+y,fd(ans[a[x]]),sz);
20 }
21 }
完整代码:
1 #include <bits/stdc++.h>
2
3 using namespace std;
4
5 #define MP make_pair
6 #define PB push_back
7 #define ll first
8 #define rr second
9 typedef long long LL;
10 typedef pair<int,int> PII;
11 const double eps=1e-8;
12 const double pi=acos(-1.0);
13 const int K=1e6+7;
14 const int mod=1e9+7;
15
16
17 int n,a[K],b[K],sum[K],ans[K];
18 int ha[K],hb[K];
19
20 int fd(int x)
21 {
22 return sum[x]==2?fd(ans[x]):x;
23 }
24 void solve(int x,int y,int fa,int sz)
25 {
26 if(x>sz)return;
27 ans[a[x]]=ans[b[y]]=fa;
28 if(a[x]==b[y]) sum[fa]+=1;
29 else sum[fa]+=2;
30 if(x==sz)return;
31 if(a[x]==b[y])
32 solve(x+1,y+1,a[x],sz);
33 else
34 {
35 int ta,tb;
36 ta=ha[b[y]]-1,tb=hb[a[x]]-y+ta;
37 if(x!=ta)
38 solve(x+1,hb[a[x]]+1,a[x],ta);
39 if(y!=hb[a[x]]-1)
40 solve(ta+2,y+1,b[y],tb);
41 if(tb!=sz)
42 solve(tb+1,tb+1-x+y,fd(ans[a[x]]),sz);
43 }
44 }
45 int main(void)
46 {
47 std::ios::sync_with_stdio(false);
48 std::cin.tie(0);
49 int t;
50 cin>>t;
51 while(t--)
52 {
53 cin>>n;
54 for(int i=1;i<=n;i++)
55 cin>>a[i],ha[a[i]]=i,sum[i]=0;
56 for(int i=1;i<=n;i++)
57 cin>>b[i],hb[b[i]]=i;
58 solve(1,1,0,n);
59 for(int i=1;i<n;i++)
60 cout<<ans[i]<<" ";
61 cout<<ans[n]<<endl;
62 }
63 return 0;
64 }