在上一篇中已经介绍了用链表实现约瑟夫环的问题,博文:http://www.cnblogs.com/webor2006/p/7102568.html
其实它还有一种更加简便更加容易理解的实现方式,那就是用数组,当然这两种实现方式的时间复杂度一样,其实现思路跟用链表的基本上类似,下面整理一下:
首先用数组表达一个环,这就没有链表那么麻烦了,还是用四个人围着一个桌子在做淘汰游戏为例:
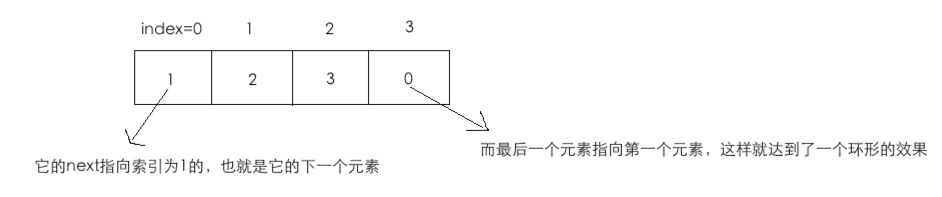

具体生成的伪代码比较简单:
for(int i = 0; i < 数组长度; i++){ next_persons[i] = (i + 1) % 数组长度; //为什么要取模,因为最后一个元素得链到第一个元素达到环形的效果 }
所以先把代码框架可以先写好:

接着来整理一下最核心的淘汰逻辑,其实基本上跟用链表实现的思路类似:
这里还是以数3就淘汰的规则来整理【从第一个元素开始数数】:

1、首先判断边界条件:如果数组只剩最后一个元素时,则没必要进行数数了,因为数组不可能为null,不像链表一样,而用代码如何来表示呢?
2、首先数3-1=2下,原因跟链表实现类似,是为了取出真正要淘汰的元素:

3、获得要淘汰的元素next_persons[当前数数的index],并将next_persion[当前数数的index]=next_persion[2]=next_persion[next_persion[当前数数的index]]。
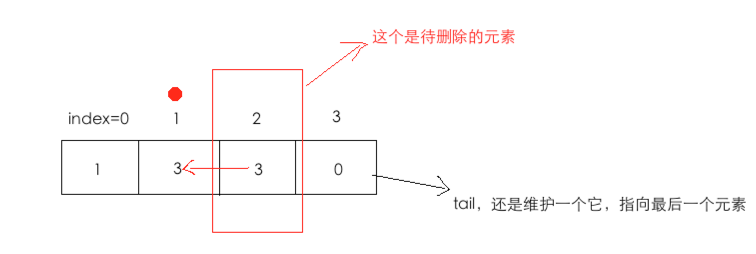
4、在删除index=2之前,有一种特珠情况需要注意,如图:

那在删除index=3之前,首先需要将tail指向p,也就是index=2,不然到的把index=3删掉了tail整个状态就不对了,这是需要注意到的。
5、由于是数组,所以不涉及到链表真正的delete操作,只要将其孤立起来既可,不用做任何一些释放的操作。
纵观以上步骤跟链表的实现思路真的大同小异,下面具体看实现代码:
#include<iostream> class joseph_circle { int* next_persons;//主要是用来记录下一个节点 int circle_length;//总元素个数 int tail;//尾结点,默认指向元素最后一位 public: joseph_circle(int circle_length): circle_length(circle_length) { next_persons = new int[circle_length]; //生成环形数据 for (int i = 0; i < circle_length; ++i){ next_persons[i] = (i + 1) % circle_length; } tail = circle_length - 1; } ~joseph_circle() { } void output() { int p = tail; while(true){ p = next_persons[p]; std::cout << p << " "; if(p == tail) break; //reach the last element of the circle } std::cout << std::endl; } //淘汰逻辑的核心方法,动态根据传的值来进行淘汰 void eliminate(int step) { int p = tail; while(next_persons[p] != p) { //1、首先进行数数,只要step-1既可,因为要在淘汰之前将要淘汰的数据先拿到 for (int i = 0; i < step - 1; ++i){ p = next_persons[p]; } //2、将要淘汰的元素孤立起来 int eliminated_node = next_persons[p]; next_persons[p] = next_persons[next_persons[p]]; //3、在淘汰之前需要注意一种特珠情况 if(eliminated_node == tail) { tail = p; } std::cout << "deleting:" << eliminated_node <<std::endl; output(); } } }; int main(void) { joseph_circle circle(6); circle.eliminate(3);//数到3就淘汰 return 0; }
编译运行:

而时间复杂度由于跟用链表实现的一样,所以这里不分析了,具体可以参考上篇博客。