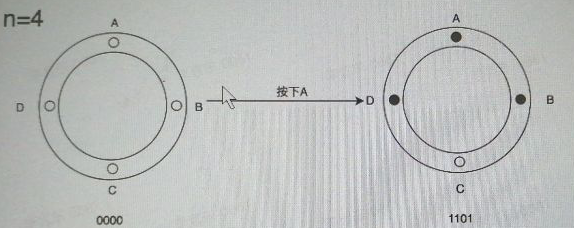
已知圆环上均匀分布着n个开关,开关按下后,按下的开关和其相邻的开关状态会同时发生切换(1->0/0->1),给定各开关的初始状态,输出将开关全部置为1所需的最少操作数
输入
第一行输入为时,N表示圆环上的开关数量,第二行有N个数字,表示每个开关的状态x (顺时针),1< N <- 16, x为0或1
输出
对于每组测试数据,输出最少所需的操作次数,如果无法将开关全部置为1请输出-1, 输出中不要包含多余
输入
10
0110001001
输出
4
说明
0110001001->
1000001001->
1111001001->
1111110001->
1111111111
思路:枚举所有能全亮的翻转方案,逐个检查
#include<bits/stdc++.h>
using namespace std;
const int N=17;
int n, ans=INT_MAX, a[N], rev[N];
void dfs(int d) {
if (d == n) {
int t[n]; for (int i=0; i<n; i++) t[i]=a[i];
for (int i=0; i<n; i++) {
if (rev[i]) {
t[(i-1+n)%n]^=1;
t[i]^=1;
t[(i+1)%n]^=1;
}
}
if (all_of(t,t+n,[&](int st){return st==1;})) {
ans=min(ans, accumulate(rev,rev+n,0));
}
return;
}
rev[d]=false;
dfs(d+1);
rev[d]=true;
dfs(d+1);
}
int main() {
std::ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
cin>>n; string s; cin>>s; //注意:输入数字是连着的
for (int i=0; i<n; i++) a[i]=s[i]-'0';
dfs(0);
if (ans==INT_MAX) cout<<-1;
else cout<<ans;
return 0;
}