• 5. Longest Palindromic Substring

    Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.

    寻找最长回文子串

    Example:

    Input: "babad"

Output: "bab"

Note: "aba" is also a valid answer.

    Example:

    Input: "cbbd"

Output: "bb"

    Brute Force

    Time complexity O(n3)
    判断每个子串是否是回文字符串，遍历每个子串O(n2)，判断是否回文串O(n)

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    class Solution {
    public:
        string longestPalindrome(string s) {
            int max = 0, maxi = 0, maxc = 0;
            for (int i = 0; i< s.size(); ++i) {
                for (int j = 1; i + j - 1< s.size(); ++j) {
                    if (isPalindromic(s.substr(i, j)))
                        if (j> max) {
                            max = j;
                            maxi = i;
                            maxc = j;
                        }
                }
            }
            return s.substr(maxi, maxc);
        }
        bool isPalindromic(string s) {
            for (int i = 0; i < s.size() / 2; ++i) {
                if (s[i] != s[s.size() - 1- i])
                    return false;
            }
            return true;
        }
    };

    但是字符串过长，会超时

    Dynamic Programming

    time O(n2), Space O(n2)
    递推关系，描述如下：
    1. 定义 P[ i, j ] ← 如果子串Si … Sj 是一个回文，那么该项为true, 否则为false
    因此递推如下：
    1. P[ i, j ] 为 true ← ( P[ i+1, j-1 ]为true，并且Si = Sj )
    基本条件是：
    1. P[ i, i ] 一定是true
    2. P[ i, i+1 ] 为true ← ( Si = Si+1 )
    这便是一个典型的DP问题解法。首先初始化长度为1,2的回文字符判断表，即P。然后以它为基础，逐个找出长度为3,4,5……的回文。
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    string longestPalindromeDP(string s) {
      int n = s.length();
      int longestBegin = 0;
      int maxLen = 1;
      bool table[1000][1000] = {false};
      for (int i = 0; i < n; i++) {
        table[i][i] = true;
      }
      for (int i = 0; i < n-1; i++) {
        if (s[i] == s[i+1]) {
          table[i][i+1] = true;
          longestBegin = i;
          maxLen = 2;
        }
      }
      for (int len = 3; len <= n; len++) {//对长度为3,4,5……的子串进行遍历
        for (int i = 0; i < n-len+1; i++) {//以len为窗口，在s上进行平移，判断是否符合递推条件
          int j = i+len-1;
          if (s[i] == s[j] && table[i+1][j-1]) {
            table[i][j] = true;
            longestBegin = i;
            maxLen = len;
          }
        }
      }
      return s.substr(longestBegin, maxLen);
    }

    举例：cabccbad

    第一次循环以后，table值如下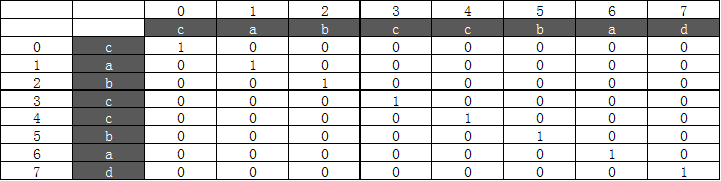

    第二次循环以后，table值如下：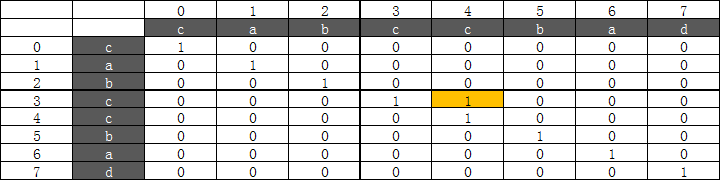

    下面开始长度为3,4,5……的循环：
    1. len=3：
    　　
         窗口里的子串为cab，i=0，j=2，这时候判断 Table[1][1] 是否 true（是），并且 s[0] 和 s[2] 是否相等（ 不相等）所以不满足。窗口平移：
    　　
         一样的判断，同理还是不满足。
    ……
    len=3循环结束，table值不变，因为没有长度为3的回文串。

    2. len=4：
     　 
         窗口子串为”cabc“，此时i=0，j=3，Table[1][2] false，不匹配。窗口平移。
         
         窗口子串为”abcc“，此时i=1，j=4，Table[2][3] false，不匹配。窗口平移。
    　  
         窗口子串为”bccb“，此时i=2，j=5，Table[3][4] true，且 s[2]==s[5]，maxlen=4，longestBegin=2，Table更新
    　　

    3. 后面都不更新。
    4. len=6：
         当窗口滑到
    　
         串口子串为”abccba“，此时i=1，j=6，Table[2][5] true，且 s[1]==s[6]，maxlen=6，longestBegin=1，Table更新
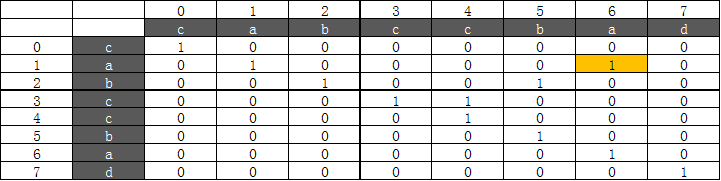
    5. len=7：
        不更新。

    DP改进

    事实上我们可以在O(N2)时间复杂度的前提下，不使用额外的存储空间。
    可以观察到，一个回文是以中心点，镜像对称的。因此，一个回文可以从中心点展开，而这个中心点，有2N-1个。
    可能你会问，为什么是2N-1个中心点，而不是N个。这是因为偶数串中心点是两个数中间，奇数串中心点是中间的数字。
    因为在一个中心点展开回文，需要耗时O(N)，总共时间复杂度也就是O(N2).
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    class Solution {
    public:
        string longestPalindrome(string s) {
            int len = s.size();
            if (len == 0) return "";
            string longest;
            for(int i = 0; i < len; ++i){
                string s1 = expand(s,i,i);
                if(s1.size() > longest.size()) longest = s1;
                string s2 = expand(s,i,i+1);
                if(s2.size() > longest.size()) longest = s2;
            }
            return longest;
        }
        string expand(string s, int l, int r){
            int len = s.size();
            while(l>=0 && r < len && s[l] == s[r]){
                --l;
                ++r;
            }
            return s.substr(l+1, r - l -1);
        }
    };

    举例：cabccbad

    初始时，i=0 （奇 代表奇数长子串，偶 代表偶数长子串）

    　 奇：
              一次循环，l=-1，r=1
              s.substr(l+1,r-l-1)==s.substr(0,1)，即”c“->longest
         偶：
              不满足循环条件，l=0，r=1
              substr(1,0) null.
    i=1:
         奇：
               同上
         偶：
               同上
    ……
    i=3：
         奇：
              同上
         偶：
              可以看出这是回文的对称点。
              循环三次，第四次判断结束。
              l=0，r=7
              substr(1，6）：”abccba“ -> longest
    ……

    Manacher算法

    time complexity O(n)
    space comlexity O(n)
    1. 计算P[i]
    2. 扩展P[i]
    3. 扩展边界R，C
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    // Transform S into T.
    // For example, S = "abba", T = "^#a#b#b#a#$".
    // ^ and $ signs are sentinels appended to each end to avoid bounds checking
    string preProcess(string s) {
      int n = s.length();
      if (n == 0) return "^$";
      string ret = "^";
      for (int i = 0; i < n; i++)
        ret += "#" + s.substr(i, 1);
      
      ret += "#$";
      return ret;
    }
      
    string longestPalindrome(string s) {
      string T = preProcess(s);
      int n = T.length();
      int *P = new int[n];
      int C = 0, R = 0;
      for (int i = 1; i < n-1; i++) {
        int i_mirror = 2*C-i; // equals to i' = C - (i-C)
         
        P[i] = (R > i) ? min(R-i, P[i_mirror]) : 0;
         
        // Attempt to expand palindrome centered at i
        if(i + P[i] >= R) // There's no need to expand palindrome when i + P[i] < R
        while (T[i + 1 + P[i]] == T[i - 1 - P[i]])
          P[i]++;
      
        // If palindrome centered at i expand past R,
        // adjust center based on expanded palindrome.
        if (i + P[i] > R) {
          C = i;
          R = i + P[i];
        }
      }
      
      // Find the maximum element in P.
      int maxLen = 0;
      int centerIndex = 0;
      for (int i = 1; i < n-1; i++) {
        if (P[i] > maxLen) {
          maxLen = P[i];
          centerIndex = i;
        }
      }
      delete[] P;
       
      return s.substr((centerIndex - 1 - maxLen)/2, maxLen);
    }

    初始化：
    1.    R       
    2.    C
    3.      i
    4. T: ^ # b # a # b # c #  b  #  a  #  b  #  c  #  b  #  a  #  c  #  c  #  b  #  a  # $
    5. P: 
    6.    0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
    i = 1
    1.      R       
    2.      C
    3.      i
    4. T: ^ # b # a # b # c #  b  #  a  #  b  #  c  #  b  #  a  #  c  #  c  #  b  #  a  # $
    5. P:   0
    6.    0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
    i = 2
    计算P[i]
    1.    R       
    2.    C
    3.        i
    4. T: ^ # b # a # b # c #  b  #  a  #  b  #  c  #  b  #  a  #  c  #  c  #  b  #  a  # $
    5. P:   0 0
    6.    0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
    扩展P[i]
    1.    R       
    2.    C
    3.        i
    4. T: ^ # b # a # b # c #  b  #  a  #  b  #  c  #  b  #  a  #  c  #  c  #  b  #  a  # $
    5. P:   0 1
    6.    0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
    扩展边界
    1.          R       
    2.        C
    3.        i
    4. T: ^ # b # a # b # c #  b  #  a  #  b  #  c  #  b  #  a  #  c  #  c  #  b  #  a  # $
    5. P:   0 1
    6.    0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
    i = 3
    1.          R       
    2.        C
    3.          i
    4. T: ^ # b # a # b # c #  b  #  a  #  b  #  c  #  b  #  a  #  c  #  c  #  b  #  a  # $
    5. P:   0 1 0
    6.    0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
    i = 4
    1.                  R       
    2.            C
    3.            i
    4. T: ^ # b # a # b # c #  b  #  a  #  b  #  c  #  b  #  a  #  c  #  c  #  b  #  a  # $
    5. P:   0 1 0 3
    6.    0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
    i = 5
    1.                  R       
    2.            C
    3.          i'  i
    4. T: ^ # b # a # b # c #  b  #  a  #  b  #  c  #  b  #  a  #  c  #  c  #  b  #  a  # $
    5. P:   0 1 0 3 0
    6.    0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
    i = 6
    1.                  R       
    2.            C
    3.        i'      i
    4. T: ^ # b # a # b # c #  b  #  a  #  b  #  c  #  b  #  a  #  c  #  c  #  b  #  a  # $
    5. P:   0 1 0 3 0 1
    6.    0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
    i = 8
    1.                                        R       
    2.                    C
    3.                    i
    4. T: ^ # b # a # b # c #  b  #  a  #  b  #  c  #  b  #  a  #  c  #  c  #  b  #  a  # $
    5. P:   0 1 0 3 0 1 0 7
    6.    0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
    i = 9
    1.                                        R       
    2.                    C
    3.            i'                 i
    4. T: ^ # b # a # b # c #  b  #  a  #  b  #  c  #  b  #  a  #  c  #  c  #  b  #  a  # $
    5. P:   0 1 0 3 0 1 0 7 0  1  0  9
    6.    0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
  • 相关阅读:
    线性表单链表的实现
    线性表顺序存储结构
    【C语言】产生随机数
    TCP/IP协议
    【bfs】奇怪的电梯（P1135）
    【DFS】取数游戏(P1123)
    【DFS】圣诞夜的极光（P1454）
    【贪心】骑士的工作(P2695)
    【贪心】纪念品分组（P1094）
    生活的那么一点反思
  • 原文地址：https://www.cnblogs.com/zhxshseu/p/94882e9ef7cddcc48293c9e617c81284.html
Copyright © 2020-2023  润新知