Sorting Slides
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 5390 | Accepted: 2095 |
Description
Professor Clumsey is going to give an important talk this afternoon. Unfortunately, he is not a very tidy person and has put all his transparencies on one big heap. Before giving the talk, he has to sort the slides. Being a kind of minimalist, he wants to do this with the minimum amount of work possible.
The situation is like this. The slides all have numbers written on them according to their order in the talk. Since the slides lie on each other and are transparent, one cannot see on which slide each number is written.
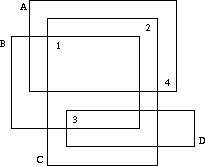
Well, one cannot see on which slide a number is written, but one may deduce which numbers are written on which slides. If we label the slides which characters A, B, C, ... as in the figure above, it is obvious that D has number 3, B has number 1, C number 2 and A number 4.
Your task, should you choose to accept it, is to write a program that automates this process.
The situation is like this. The slides all have numbers written on them according to their order in the talk. Since the slides lie on each other and are transparent, one cannot see on which slide each number is written.

Well, one cannot see on which slide a number is written, but one may deduce which numbers are written on which slides. If we label the slides which characters A, B, C, ... as in the figure above, it is obvious that D has number 3, B has number 1, C number 2 and A number 4.
Your task, should you choose to accept it, is to write a program that automates this process.
Input
The input consists of several heap descriptions. Each heap descriptions starts with a line containing a single integer n, the number of slides in the heap. The following n lines contain four integers xmin, xmax, ymin and ymax, each, the bounding coordinates of the slides. The slides will be labeled as A, B, C, ... in the order of the input.
This is followed by n lines containing two integers each, the x- and y-coordinates of the n numbers printed on the slides. The first coordinate pair will be for number 1, the next pair for 2, etc. No number will lie on a slide boundary.
The input is terminated by a heap description starting with n = 0, which should not be processed.
This is followed by n lines containing two integers each, the x- and y-coordinates of the n numbers printed on the slides. The first coordinate pair will be for number 1, the next pair for 2, etc. No number will lie on a slide boundary.
The input is terminated by a heap description starting with n = 0, which should not be processed.
Output
For each heap description in the input first output its number. Then print a series of all the slides whose numbers can be uniquely determined from the input. Order the pairs by their letter identifier.
If no matchings can be determined from the input, just print the word none on a line by itself.
Output a blank line after each test case.
If no matchings can be determined from the input, just print the word none on a line by itself.
Output a blank line after each test case.
Sample Input
4
6 22 10 20
4 18 6 16
8 20 2 18
10 24 4 8
9 15
19 17
11 7
21 11
2
0 2 0 2
0 2 0 2
1 1
1 1
0
Sample Output
Heap 1
(A,4) (B,1) (C,2) (D,3)
Heap 2
none
Source
Southwestern European Regional Contest 1998
Solution
题意就是找所有可以唯一对应起来的矩形和数字。
看起来这种对应关系很像二分图匹配??
建成二分图后就变成判定哪些边是必须的了。必须的意思是删掉这条边最大匹配数会变小,所以对所有边删边后做一次最大匹配,与最初始的最大匹配数进行比较即可。
Code
#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> using namespace std; int n, vis[2005], to[2005], pi[2005]; int xi[1005], xa[1005], yi[1005], ya[1005]; bool check(int x, int y, int i) { if(x >= xi[i] && x <= xa[i] && y >= yi[i] && y <= ya[i]) return 1; return 0; } int G[1005][2005]; bool dfs(int u) { for(int v = 1; v <= n; v ++) { if(G[u][v]) { if(!vis[v]) { vis[v] = 1; if(!pi[v] || dfs(pi[v])) { pi[v] = u; to[u] = v; return 1; } } } } return 0; } int match() { memset(to, 0, sizeof(to)); memset(pi, 0, sizeof(pi)); int ans = 0; for(int i = 1; i <= n; i ++) { if(!to[i]) { memset(vis, 0, sizeof(vis)); ans += dfs(i); } } return ans; } int main() { int ti = 0; while(~scanf("%d", &n)) { if(n == 0) break; memset(G, 0, sizeof(G)); for(int i = 1; i <= n; i ++) scanf("%d%d%d%d", &xi[i], &xa[i], &yi[i], &ya[i]); for(int i = 1; i <= n; i ++) { int x, y; scanf("%d%d", &x, &y); for(int j = 1; j <= n; j ++) { if(!check(x, y, j)) continue; G[j][i] = 1; } } int ma = match(); int flag = 0; printf("Heap %d ", ++ ti); for(int i = 1; i <= n; i ++) { for(int j = 1; j <= n; j ++) if(G[i][j]) { G[i][j] = 0; if(match() < ma) { printf("(%c,%d) ", i + 64, j); flag = 1; } G[i][j] = 1; } } if(!flag) printf("none "); else printf(" "); } return 0; }