经典传染病传播模型

目前阅读的论文里都少不了对动力学的研究，而其中最经典的当属传染病传播动力学，本篇文章对此做一个简单的模型构建记录。

首先了解群体中有三种状态的个体：

（1）易感状态 S （Susceptible），处于该状态的个体是有可能被感染的个体。

（ 2）感染状态 I （Infected），处于该状态的个体是已经被病毒感染的个体，同时该个体还有可能将病毒传播给易感状态的个体。

（3）移除状态 R（Recovered），处于该状态的个体是已经治愈的个体，同时该个体获得了免疫力，不会再被同种病毒再感染。

下面建立 SI、SIS、SIR 三种经典的传染病模型。

构建模型可以参考以下3篇文章：

[1] https://www.kesci.com/mw/project/60161bf6ac79f40016b7d7d9

[2] https://blog.csdn.net/qq_42839893/article/details/113464402

[3] https://zhuanlan.zhihu.com/p/104091330

1、SI传染病模型

SI模型图及其微分方程表示：

import scipy.integrate as spi
import numpy as np
import matplotlib.pyplot as plt

# N为人群总数
N = 10000
# β为传染率系数
beta = 0.25
# gamma为恢复率系数
gamma = 0
# I_0为感染者的初始人数
I_0 = 1
# S_0为易感者的初始人数
S_0 = N - I_0
# T为传播时间
T = 150

# INI为初始状态下的数组
INI = (S_0,I_0)


def funcSI(inivalue,_):
    Y = np.zeros(2)
    X = inivalue
    # 易感个体变化
    Y[0] = - (beta * X[0] * X[1]) / N + gamma * X[1]
    # 感染个体变化
    Y[1] = (beta * X[0] * X[1]) / N - gamma * X[1]
    return Y

T_range = np.arange(0,T + 1)

RES = spi.odeint(funcSI,INI,T_range)


plt.plot(RES[:,0],color = 'darkblue',label = 'Susceptible',marker = '.')
plt.plot(RES[:,1],color = 'red',label = 'Infection',marker = '.')
plt.title('SI Model')
plt.legend()
plt.xlabel('Day')
plt.ylabel('Number')
plt.show()

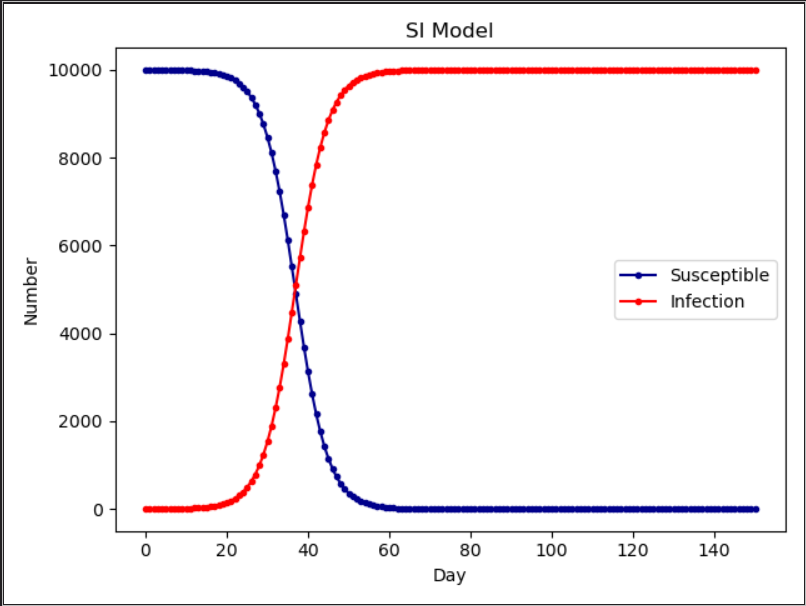
2、SIS传染病模型

SIS模型图及其微分方程表示：

import scipy.integrate as spi
import numpy as np
import matplotlib.pyplot as plt

# N为人群总数
N = 10000
# β为传染率系数
beta = 0.25
# gamma为恢复率系数
gamma = 0.05
# I_0为感染者的初始人数
I_0 = 1
# S_0为易感者的初始人数
S_0 = N - I_0
# T为传播时间
T = 150

# INI为初始状态下的数组
INI = (S_0,I_0)


def funcSIS(inivalue,_):
    Y = np.zeros(2)
    X = inivalue
    # 易感个体变化
    Y[0] = - (beta * X[0]) / N * X[1] + gamma * X[1]
    # 感染个体变化
    Y[1] = (beta * X[0] * X[1]) / N - gamma * X[1]
    return Y

T_range = np.arange(0,T + 1)

RES = spi.odeint(funcSIS,INI,T_range)


plt.plot(RES[:,0],color = 'darkblue',label = 'Susceptible',marker = '.')
plt.plot(RES[:,1],color = 'red',label = 'Infection',marker = '.')
plt.title('SIS Model')
plt.legend()
plt.xlabel('Day')
plt.ylabel('Number')
plt.show()

3、SIR传染病模型

SIR模型图及其微分方程表示：

import scipy.integrate as spi
import numpy as np
import matplotlib.pyplot as plt

# N为人群总数
N = 10000
# β为传染率系数
beta = 0.25
# gamma为恢复率系数
gamma = 0.05
# I_0为感染者的初始人数
I_0 = 1
# R_0为治愈者的初始人数
R_0 = 0
# S_0为易感者的初始人数
S_0 = N - I_0 - R_0
# T为传播时间
T = 150

# INI为初始状态下的数组
INI = (S_0,I_0,R_0)


def funcSIR(inivalue,_):
    Y = np.zeros(3)
    X = inivalue
    # 易感个体变化
    Y[0] = - (beta * X[0] * X[1]) / N
    # 感染个体变化
    Y[1] = (beta * X[0] * X[1]) / N - gamma * X[1]
    # 治愈个体变化
    Y[2] = gamma * X[1]
    return Y

T_range = np.arange(0,T + 1)

RES = spi.odeint(funcSIR,INI,T_range)


plt.plot(RES[:,0],color = 'darkblue',label = 'Susceptible',marker = '.')
plt.plot(RES[:,1],color = 'red',label = 'Infection',marker = '.')
plt.plot(RES[:,2],color = 'yellow',label = 'Recovery',marker = '.')
plt.title('SIR Model')
plt.legend()
plt.xlabel('Day')
plt.ylabel('Number')
plt.show()