一、认识拓扑排序
在一个有向图中找到一个拓扑序列的过程称之为拓扑排序
即对有向图的顶点排成一个线性序列
结合李春葆数据结构延伸一个非常好的例子,学习Java系列的教程
| 代号 | 科目 | 学前需掌握 |
|---|---|---|
| A1 | java基础 | |
| A2 | html | |
| A3 | Jsp | A1,A2 |
| A4 | servlet | A1 |
| A5 | ssm | A3,A4 |
| A6 | springboot | A5 |
就比如学习java系列要从java基础,到jsp/servlet,到ssm,到springboot,springcloud等是个循序渐进且有依赖的过程。在jsp学习要首先掌握java基础和html基础。学习框架要掌握jsp/servlet和jdbc之类才行。那么,这个学习过程即构成一个拓扑序列。当然这个序列也不唯一,你可以对不关联的学科随意选择顺序(比如html和java可以随便先开始哪一个。)
那上述序列可以简单表示为:
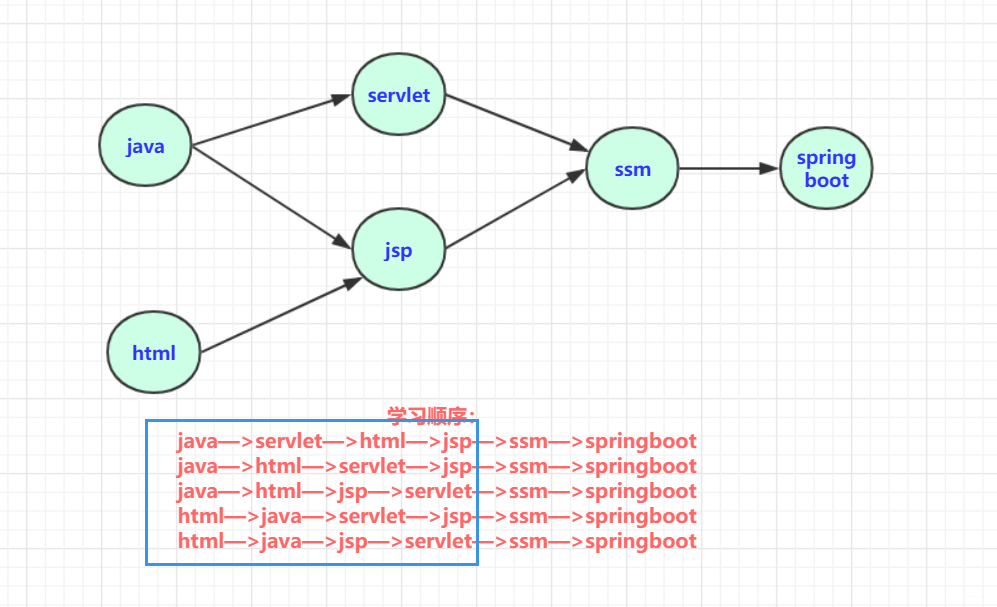
其中五种均为可以选择的学习方案,对课程安排可以有参考作用,当然,五个都是拓扑序列。只是选择的策略不同!
DGA:有向无环图(Directed Acyclic Graph,DGA)
AOV网:这种用顶点表示活动,用有向边表示活动之间有点关系的有向图称为顶点表示活动的网(activity on vertex network ,AOV网)
二、拓扑排序算法分析和实现
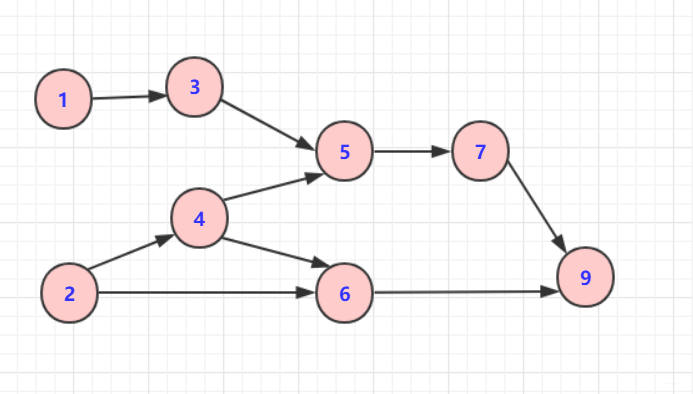
正常步骤为(方法不一定唯一):
- 从DGA图中找到一个
没有前驱的顶点(入度为0)输出。(可以遍历,也可以用优先队列维护) - 删除以这个点为起点的边。(它的指向的边删除,为了找到下个没有前驱的顶点)
- 重复上述,直到最后一个顶点被输出。如果还有顶点未被输出,则说明有环!
对于上图的简单序列,可以简单描述步骤为:
1:删除1或2输出

2:删除2或3以及对应边
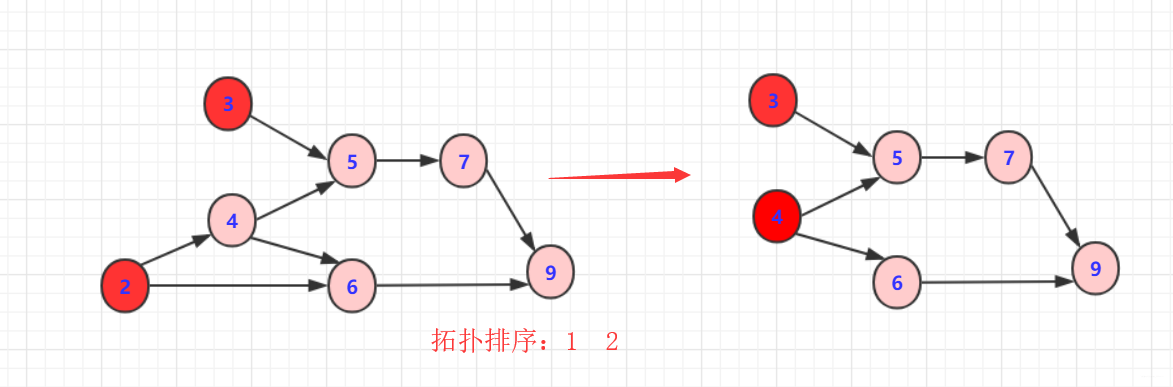
3:删除3或者4以及对应边
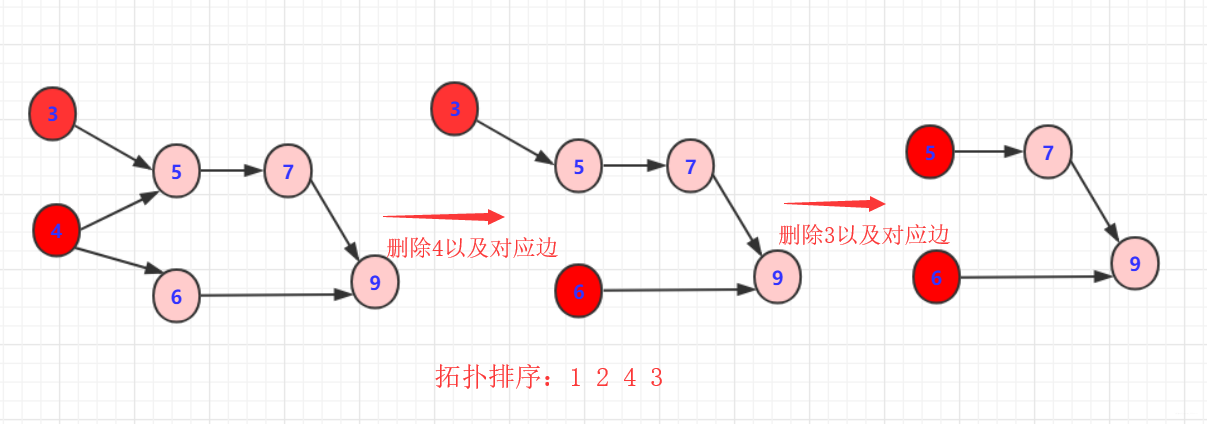
4:重复以上规则步骤
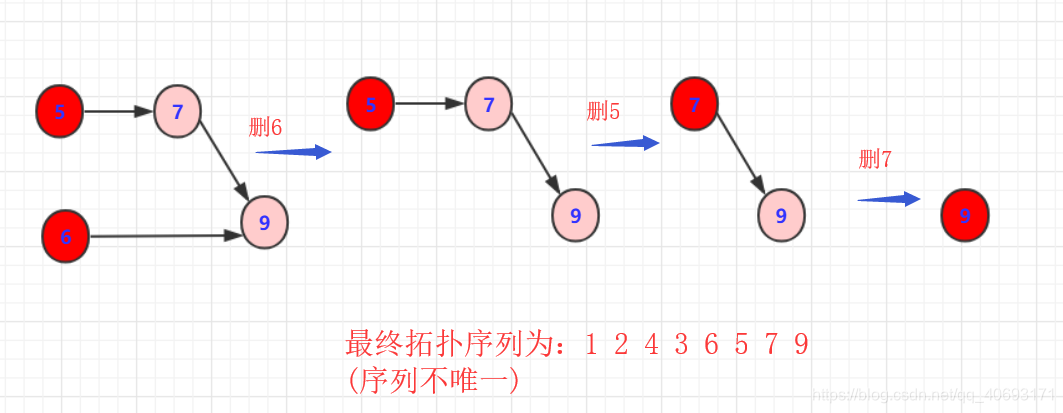
这样就完成一次拓扑排序,得到一个拓扑序列,但是这个序列并不唯一!从过程中也看到有很多选择方案,具体得到结果看你算法的设计了。但只要满足即是拓扑排序序列。
Java代码实现:
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.List;
import java.util.Queue;
import java.util.Stack;
/**
* 实现流程参考博客园博主bigsai
*
*/
public class TuoPu {
static class node
{
int value; //结点数值
List<Integer> next; //list集合替代链表
public node(int value) {
this.value=value;
next=new ArrayList<Integer>();
}
public void setnext(List<Integer>list) { //指向
this.next=list;
}
}
public static void main(String[] args) {
node []nodes=new node[9];//储存节点
int a[]=new int[9];//储存入度
List<Integer>list[]=new ArrayList[10];//临时空间,为了存储指向的集合
for(int i=1;i<9;i++)
{
nodes[i]=new node(i);
list[i]=new ArrayList<Integer>();
}
initmap(nodes,list,a);
//主要流程
//Queue<node>q1=new ArrayDeque<node>();
Stack<node>s1=new Stack<node>();
for(int i=1;i<9;i++)
{
//System.out.print(nodes[i].next.size()+" 55 ");
//System.out.println(a[i]);
if(a[i]==0) {s1.add(nodes[i]);} //扫描一遍所有node 将所有入度为0的点加入一个栈
}
//当栈(队列)不空的时候,抛出其中任意一个node(栈就是尾,队就是头,顺序无所谓,上面分析了只要同时入度为零可以随便选择顺序)
//将node输出,并且node指向的所有元素入度减一。如果某个点的入度被减为0,那么就将它加入栈
while(!s1.isEmpty())
{
node n1=s1.pop();//抛出输出
System.out.print(n1.value+" ");
List<Integer>next=n1.next;
for(int i=0;i<next.size();i++)
{
a[next.get(i)]--;//入度减一
if(a[next.get(i)]==0)//如果入度为0
{
s1.add(nodes[next.get(i)]);
}
}
}
}
private static void initmap(node[] nodes, List<Integer>[] list, int[] a) {
list[1].add(3);
nodes[1].setnext(list[1]);
a[3]++;
list[2].add(4);list[2].add(6);
nodes[2].setnext(list[2]);
a[4]++;a[6]++;
list[3].add(5);
nodes[3].setnext(list[3]);
a[5]++;
list[4].add(5);list[4].add(6);
nodes[4].setnext(list[4]);
a[5]++;a[6]++;
list[5].add(7);
nodes[5].setnext(list[5]);
a[7]++;
list[6].add(8);
nodes[6].setnext(list[6]);
a[8]++;
list[7].add(8);
nodes[7].setnext(list[7]);
a[8]++;
}
}
//output:
//
//2 4 6 1 3 5 7 8
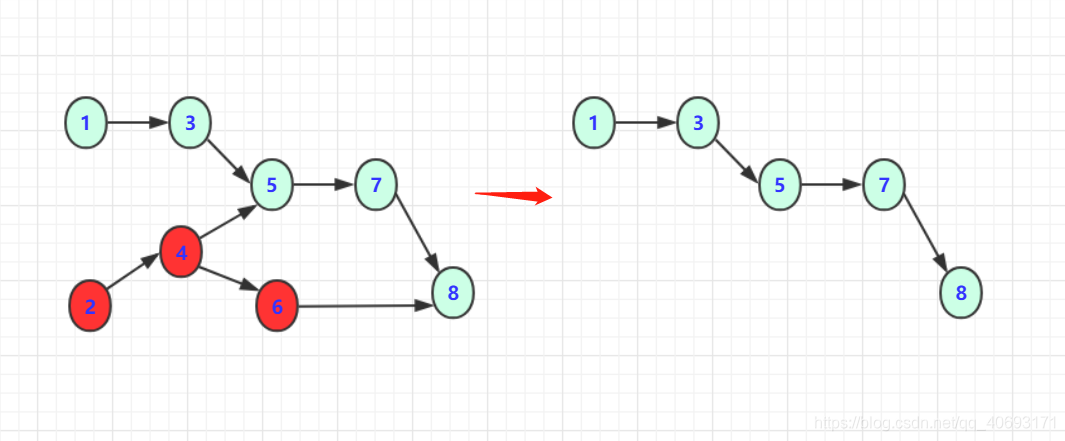
上面说过用栈和队列都可以!如果使用队列就会得到1 2 3 4 5 6 7 8的拓扑序列
三、C语言核心代码
代码学习于王道数据结构,仅供参考。
1、TuoPu
bool TopologicalSort(Graph G){
InitStack(S); //初始化栈,存储入度为0的顶点
for(int i=0;i<G.vexnum;i++)
if(indegree[i]==0)Push(S,i); //将所有入度为0的顶点进栈
int count=0; //计数,记录当前已经输出的顶点数
while(!IsEmpty(S)){ //栈不空,则存在入度为0的顶点
Pop(S,i); //栈顶元素出栈
pritnf(“%d”,G.adjlist[i]);
for(ArcNode *p=G.vertices[i].firstarc; p; p=p->nextarc){
v=p->adjvex; //取这条弧指向的顶点
if(!(--indegree[v]))Push(S,v); //入度减1为0,则入栈
}
}
if(count<G.vexnum)return false; //排序失败,有向图中有回路
else return true; //拓扑排序成功
}
拓扑排序对AOV图需要打印图中所有顶点,而且由于要删除边(实际没有删除,只是寻找入度为0的顶点)所以对所有边也要进行扫描,所以这个算法的时间复杂度为O (|V|+|E|)
2、扩展
对于一般的图,如果它的邻接矩阵是三角矩阵,则存在拓扑序列;反之则不一定成立
只要按照序号从小到大或者从大到小的顺序就能得到这个邻接矩阵为三角矩阵的图的拓扑序列。
上三角:0 1 2 3 下三角:3 2 1 0
