复习数据结构的二叉树遍历时,想到以前对这一块真的是头晕,有一部分原因是上课没好好听讲,也有一部分原因是自己研究代码不透彻,大概就知道是先序DLR、中序LDR、后序LRD,今天沉下心就来搞清楚这个问题。
1、二叉树顺序存储方式
想搞清楚二叉树的遍历就要从二叉树的顺序存储开始,我在前面的有写过:二叉树的顺序存储结构就是使用一维数组存储二叉树中的结点,并且结点的存储位置,就是数组的下标索引。(建议直接看图,清晰明了)
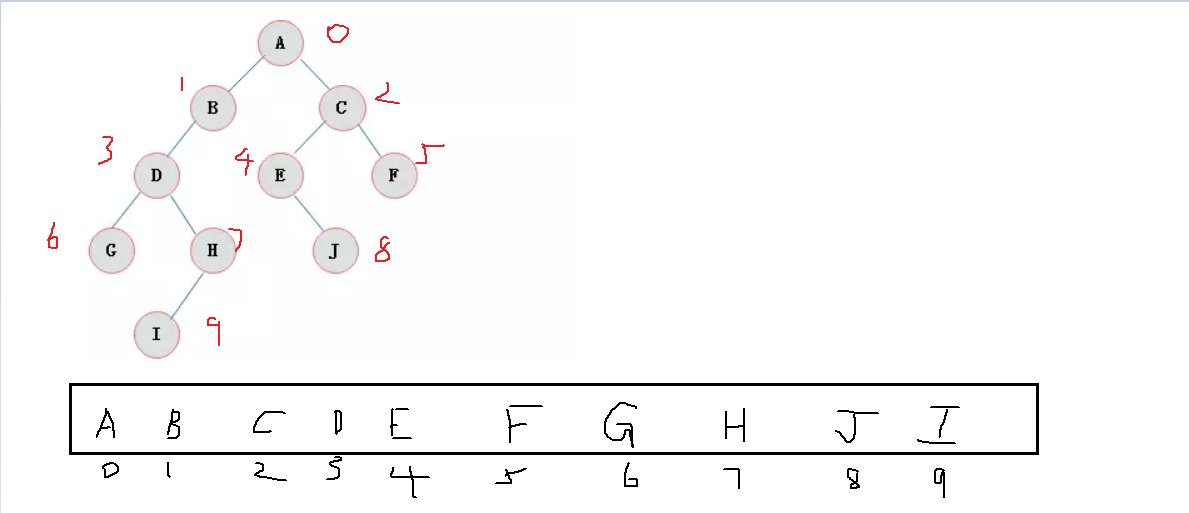
这里我们要记住:子节点的表示方法(左节点,右节点):(2i+1,2i+2)
2、递归实现
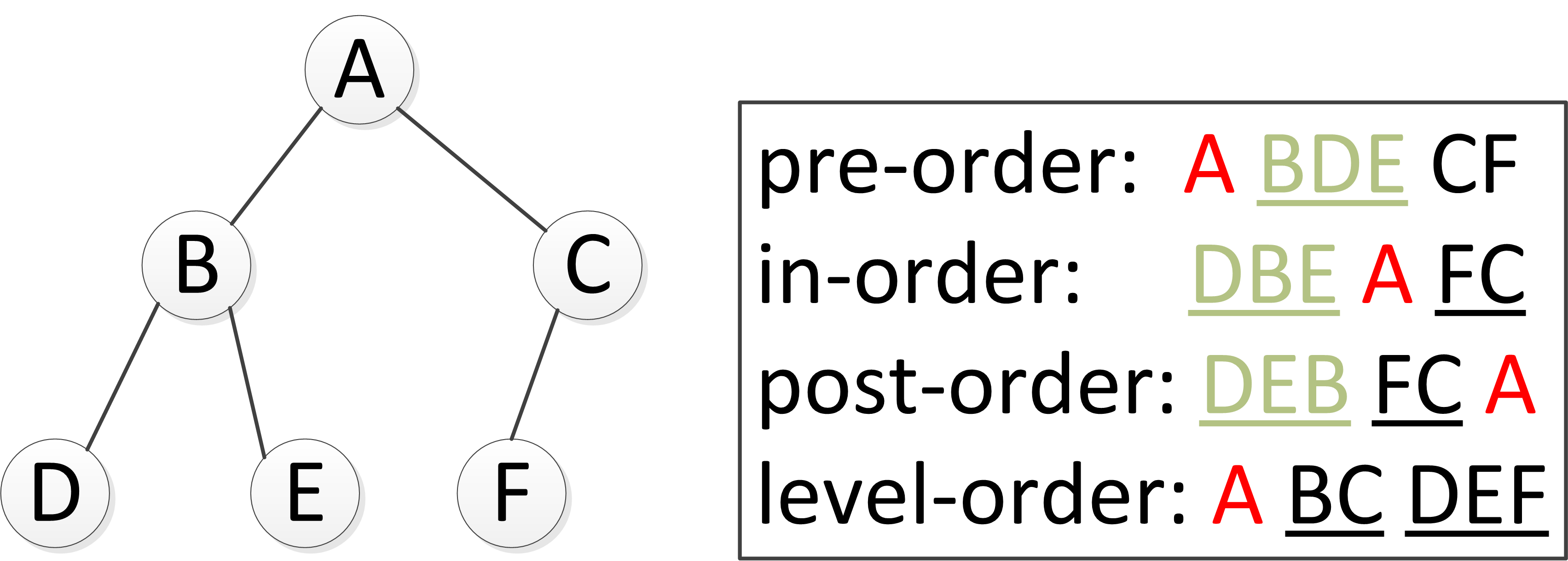
记住这个口诀(前序DLR、中序LDR、后序LRD)不是没有道理,记住子节点的表示方法也不是没有道理,我们将在递归实现中完美的展示出来,话不多说直接看代码:
/**
* create by wzm
* 递归的实现
*/
public class BinaryTree {
//先序遍历
private static void preOrder(int[] arr, int index){
if (index>=arr.length){
return;
}
System.out.println(arr[index]); //先输出根节点D
preOrder(arr, index*2+1); //输出左子树L
preOrder(arr,index*2+2); //输出右子树R
}
//中序遍历
private static void inOrder(int[] arr,int index){
if (index>=arr.length){
return;
}
inOrder(arr, index*2+1); //L
System.out.println(arr[index]); //D
inOrder(arr,index*2+2); //R
}
//后序遍历
private static void postOder(int[] arr,int index){
if (index>=arr.length){
return;
}
postOder(arr, index*2+1); //L
postOder(arr,index*2+2); //R
System.out.println(arr[index]); //D
}
//测试
public static void main(String[] args) { //index为顺序存储中根结点所在位置
int[] arr = {0,1,2,3,4,5,6,7,8,9};
preOrder(arr,0);
System.out.println("---------------------");
inOrder(arr,0);
System.out.println("---------------------");
postOder(arr,0);
}
}
结合上面提到的顺序存储,简直一目了然。
3、非递归实现
看了一些别人的博客,实现起来还是有些绕,可以运用栈的思想,当然也可以运用队列的思想,我在这里主要用栈的思想,把完成的注解写自在了代码中,边看边理解:
import java.util.Stack;
import java.util.ArrayDeque;
import java.util.Queue;
/**
* create by wzm
* 非递归的实现
*/
public class BinaryTree {
//Node节点
static class Node {
int data; //节点值
Node leftChild; //左孩子
Node rightChild; //右孩子
public Node() {
}
public Node(int data) {
this.data = data;
}
}
// create binaryTree from arrays
private static Node creatTree(int[] element, int i) {
if (i >= element.length || element[i] == -1)
return null;
Node root = new Node(element[i]);
root.leftChild = creatTree(element, i * 2 + 1);
root.rightChild = creatTree(element, i * 2 + 2);
return root;
}
/**
* 非递归先序遍历的思路如下:
* 1.先将根节点入栈
* 2.访问根节点
* 3.如果根节点存在右孩子,则将右孩子入栈
* 4.如果根节点存在左孩子,则将左孩子入栈(注意:一定是右孩子先入栈,然后左孩子入栈)
* 5.重复2~4
*
* @param root
*/
private static void preOrder(Node root) {
if (root==null)
return;
Node tmp = root;
Stack<Node> s = new Stack<>();
//1.根节点入栈
s.push(tmp);
//5.重复2~4
while (!s.empty()) {
//2.访问根节点
Node p = s.pop();
System.out.print(p.data+" ");
//3.如果根节点存在右孩子,则将右孩子入栈
if (p.rightChild!=null) {
s.push(p.rightChild);
}
//4.如果根节点存在左孩子,则将左孩子入栈
if (p.leftChild!=null) {
s.push(p.leftChild);
}
}
System.out.println();
}
/**
* 非递归中序遍历的思路如下:
* 1.先将根节点入栈
* 2.将当前节点的所有左孩子入栈,直到左孩子为空
* 3.访问栈顶元素,如果栈顶元素存在右孩子,则继续第2步
* 4.重复第2、3步,直到栈为空并且所有的节点都被访问
*
* @param root
*/
private static void inOrder(Node root) {
if (root==null)
return;
Node tmp = root;
Stack<Node> s = new Stack<>();
while (tmp!=null || !s.empty()) {
//1.先将根节点入栈
//2.将所有左孩子入栈
while (tmp!=null) {
s.push(tmp);
tmp = tmp.leftChild;
}
//3.访问栈顶元素
tmp = s.pop();
System.out.print(tmp.data+" ");
//若存在右孩子,将右孩子入栈
if (tmp.rightChild!=null) {
tmp = tmp.rightChild;
}
//否则,将tmp置为null,表示下次要访问的是栈顶元素
else {
tmp = null;
}
}
System.out.println();
}
/**
* 非递归后续遍历的实现思路:
* 1.根节点入栈
* 2.将根节点的左子树入栈,直到最左,没有左孩子为止
* 3.得到栈顶元素的值,先不访问,判断栈顶元素是否存在右孩子,如果存在并且没有被访问,则将右孩子入栈,否则,就访问栈顶元素
*
* @param root
*/
public static void postOrder(Node root) {
if (root==null)
return;
Node tmp = root;
Node prev = null; //上一次访问的结点
Stack<Node> s = new Stack<>();
while (tmp!=null || !s.empty()) {
//1.根节点及左孩子入栈
while (tmp!=null) {
s.push(tmp);
tmp = tmp.leftChild;
}
if (!s.empty()) {
//2.获取栈顶元素
tmp = s.peek();
//3.没有右孩子,或者右孩子已经被访问过
if (tmp.rightChild==null || tmp.rightChild==prev) {
//则访问栈顶元素
tmp = s.pop();
System.out.print(tmp.data+" ");
//标记上一次访问的结点
prev = tmp;
tmp = null;
}
//4.存在没有被访问的右孩子
else {
tmp = tmp.rightChild;
}
}
}
System.out.println();
}
//测试,比对递归实现,完全正确
public static void main(String[] args) {
int[] arrays = { 0, 1, 2, 3, 4, 5, 6, 7,8, 9};
Node tree = creatTree(arrays, 0);
System.out.println("测试结果:");
preOrder(tree);
System.out.println();
inOrder(tree);
System.out.println();
postOrder(tree);
System.out.println();
//levelOrder(tree);
}
}
推荐一篇结合了图片写的清晰的: https://blog.csdn.net/Benja_K/article/details/88389039 ,实现的方法有一些不一样。
4、层序遍历
从上往下打印出二叉树的每个节点,同层节点从左至右打印,最简单运用队列的思想:将本代码加入上述(非递归实现)中便可以测试
/**
* 层序遍历的实现思路:
* 1.根节点出队
* 2.左孩子不为空,则左孩子出队
* 3.之后,右孩子不为空,则右孩子出队
* 4.循环直到队空
*
* @param root
*/
public static void levelOrder(Node root) {
if (root == null) return;
Queue<Node> queue = new ArrayDeque<>();
queue.offer(root);
while (!queue.isEmpty()) {
root = queue.poll(); //逐一出队
System.out.print(root.data + " ");
if (root.leftChild != null)
queue.offer(root.leftChild);
if (root.rightChild != null)
queue.offer(root.rightChild);
}
}
5、C语言实现
考试的考点,还是自己跟着动手一下,C语言实现代码借鉴于该博客 http://data.biancheng.net/tree/
①递归遍历
#include <stdio.h>
#include<stdlib.h>
#include <string.h>
#define TElemType int
//构造结点的结构体
typedef struct BiTNode{
TElemType data;//数据域
struct BiTNode *lchild,*rchild;//左右孩子指针
}BiTNode,*BiTree;
//初始化树的函数
void CreateBiTree(BiTree *T){
*T=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->data=1;
(*T)->lchild=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->rchild=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->lchild->data=2;
(*T)->lchild->lchild=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->lchild->rchild=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->lchild->rchild->data=5;
(*T)->lchild->rchild->lchild=NULL;
(*T)->lchild->rchild->rchild=NULL;
(*T)->rchild->data=3;
(*T)->rchild->lchild=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->rchild->lchild->data=6;
(*T)->rchild->lchild->lchild=NULL;
(*T)->rchild->lchild->rchild=NULL;
(*T)->rchild->rchild=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->rchild->rchild->data=7;
(*T)->rchild->rchild->lchild=NULL;
(*T)->rchild->rchild->rchild=NULL;
(*T)->lchild->lchild->data=4;
(*T)->lchild->lchild->lchild=NULL;
(*T)->lchild->lchild->rchild=NULL;
}
//模拟操作结点元素的函数,输出结点本身的数值
void displayElem(BiTNode* elem){
printf("%d ",elem->data);
}
//先序遍历
void PreOrderTraverse(BiTree T){
if (T) {
displayElem(T);//调用操作结点数据的函数方法
PreOrderTraverse(T->lchild);//访问该结点的左孩子
PreOrderTraverse(T->rchild);//访问该结点的右孩子
}
//如果结点为空,返回上一层
return;
}
//中序遍历
void INOrderTraverse(BiTree T){
if (T) {
INOrderTraverse(T->lchild);//遍历左孩子
displayElem(T);//调用操作结点数据的函数方法
INOrderTraverse(T->rchild);//遍历右孩子
}
//如果结点为空,返回上一层
return;
}
//后序遍历
void PostOrderTraverse(BiTree T){
if (T) {
PostOrderTraverse(T->lchild);//遍历左孩子
PostOrderTraverse(T->rchild);//遍历右孩子
displayElem(T);//调用操作结点数据的函数方法
}
//如果结点为空,返回上一层
return;
}
int main() {
BiTree Tree;
CreateBiTree(&Tree);
printf("先序遍历:
");
PreOrderTraverse(Tree) ;
printf("
");
printf("中序遍历:
");
INOrderTraverse(Tree);
printf("
");
printf("后序遍历:
");
PostOrderTraverse(Tree);
}
②非递归遍历
#include <stdio.h>
#include<stdlib.h>
#include <string.h>
#define TElemType int
int top=-1;//top变量时刻表示栈顶元素所在位置
//构造结点的结构体
typedef struct BiTNode{
TElemType data;//数据域
struct BiTNode *lchild,*rchild;//左右孩子指针
}BiTNode,*BiTree;
//初始化树的函数
void CreateBiTree(BiTree *T){
*T=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->data=1;
(*T)->lchild=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->rchild=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->lchild->data=2;
(*T)->lchild->lchild=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->lchild->rchild=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->lchild->rchild->data=5;
(*T)->lchild->rchild->lchild=NULL;
(*T)->lchild->rchild->rchild=NULL;
(*T)->rchild->data=3;
(*T)->rchild->lchild=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->rchild->lchild->data=6;
(*T)->rchild->lchild->lchild=NULL;
(*T)->rchild->lchild->rchild=NULL;
(*T)->rchild->rchild=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->rchild->rchild->data=7;
(*T)->rchild->rchild->lchild=NULL;
(*T)->rchild->rchild->rchild=NULL;
(*T)->lchild->lchild->data=4;
(*T)->lchild->lchild->lchild=NULL;
(*T)->lchild->lchild->rchild=NULL;
}
//前序和中序遍历使用的进栈函数
void push(BiTNode** a,BiTNode* elem){
a[++top]=elem;
}
//弹栈函数
void pop( ){
if (top==-1) {
return ;
}
top--;
}
//模拟操作结点元素的函数,输出结点本身的数值
void displayElem(BiTNode* elem){
printf("%d ",elem->data);
}
//拿到栈顶元素
BiTNode* getTop(BiTNode**a){
return a[top];
}
//后序遍历非递归算法
typedef struct SNode{
BiTree p;
int tag;
}SNode;
//后序遍历使用的进栈函数
void postpush(SNode *a,SNode sdata){
a[++top]=sdata;
}
//先序遍历非递归算法
void PreOrderTraverse(BiTree Tree){
BiTNode* a[20];//定义一个顺序栈
BiTNode * p;//临时指针
push(a, Tree);//根结点进栈
while (top!=-1) {
p=getTop(a);//取栈顶元素
pop();//弹栈
while (p) {
displayElem(p);//调用结点的操作函数
//如果该结点有右孩子,右孩子进栈
if (p->rchild) {
push(a,p->rchild);
}
p=p->lchild;//一直指向根结点最后一个左孩子
}
}
}
//中序遍历非递归算法
void InOrderTraverse(BiTree Tree){
BiTNode* a[20];//定义一个顺序栈
BiTNode * p;//临时指针
push(a, Tree);//根结点进栈
while (top!=-1) {//top!=-1说明栈内不为空,程序继续运行
while ((p=getTop(a)) &&p){//取栈顶元素,且不能为NULL
push(a, p->lchild);//将该结点的左孩子进栈,如果没有左孩子,NULL进栈
}
pop();//跳出循环,栈顶元素肯定为NULL,将NULL弹栈
if (top!=-1) {
p=getTop(a);//取栈顶元素
pop();//栈顶元素弹栈
displayElem(p);
push(a, p->rchild);//将p指向的结点的右孩子进栈
}
}
}
//后序遍历函数
void PostOrderTraverse(BiTree Tree){
SNode a[20];//定义一个顺序栈
BiTNode * p;//临时指针
int tag;
SNode sdata;
p=Tree;
while (p||top!=-1) {
while (p) {
//为该结点入栈做准备
sdata.p=p;
sdata.tag=0;//由于遍历是左孩子,设置标志位为0
postpush(a, sdata);//压栈
p=p->lchild;//以该结点为根结点,遍历左孩子
}
sdata=a[top];//取栈顶元素
pop();//栈顶元素弹栈
p=sdata.p;
tag=sdata.tag;
//如果tag==0,说明该结点还没有遍历它的右孩子
if (tag==0) {
sdata.p=p;
sdata.tag=1;
postpush(a, sdata);//更改该结点的标志位,重新压栈
p=p->rchild;//以该结点的右孩子为根结点,重复循环
}
//如果取出来的栈顶元素的tag==1,说明此结点左右子树都遍历完了,可以调用操作函数了
else{
displayElem(p);
p=NULL;
}
}
}
int main(){
BiTree Tree;
CreateBiTree(&Tree);
printf("先序遍历:
");
PreOrderTraverse(Tree);
printf("
");
printf("中序遍历:
");
InOrderTraverse(Tree);
printf("
");
printf("后序遍历:
");
PostOrderTraverse(Tree);
printf("
");
}
③层序遍历
#include <stdio.h>
#include<stdlib.h>
#define TElemType int
//初始化队头和队尾指针开始时都为0
int front=0,rear=0;
typedef struct BiTNode{
TElemType data;//数据域
struct BiTNode *lchild,*rchild;//左右孩子指针
}BiTNode,*BiTree;
void CreateBiTree(BiTree *T){
*T=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->data=1;
(*T)->lchild=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->rchild=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->lchild->data=2;
(*T)->lchild->lchild=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->lchild->rchild=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->lchild->rchild->data=5;
(*T)->lchild->rchild->lchild=NULL;
(*T)->lchild->rchild->rchild=NULL;
(*T)->rchild->data=3;
(*T)->rchild->lchild=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->rchild->lchild->data=6;
(*T)->rchild->lchild->lchild=NULL;
(*T)->rchild->lchild->rchild=NULL;
(*T)->rchild->rchild=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->rchild->rchild->data=7;
(*T)->rchild->rchild->lchild=NULL;
(*T)->rchild->rchild->rchild=NULL;
(*T)->lchild->lchild->data=4;
(*T)->lchild->lchild->lchild=NULL;
(*T)->lchild->lchild->rchild=NULL;
}
//入队函数
void EnQueue(BiTree *a,BiTree node){
a[rear++]=node;
}
//出队函数
BiTNode* DeQueue(BiTNode** a){
return a[front++];
}
//输出函数
void displayNode(BiTree node){
printf("%d ",node->data);
}
int main() {
BiTree tree;
//初始化二叉树
CreateBiTree(&tree);
BiTNode * p;
//采用顺序队列,初始化创建队列数组
BiTree a[20];
//根结点入队
EnQueue(a, tree);
//当队头和队尾相等时,表示队列为空
while(front<rear) {
//队头结点出队
p=DeQueue(a);
displayNode(p);
//将队头结点的左右孩子依次入队
if (p->lchild!=NULL) {
EnQueue(a, p->lchild);
}
if (p->rchild!=NULL) {
EnQueue(a, p->rchild);
}
}
return 0;
}