前一篇,我们将SVM与logistic regression联系起来,这一次我们将SVM与ridge regression(之前的linear regression)联系起来。
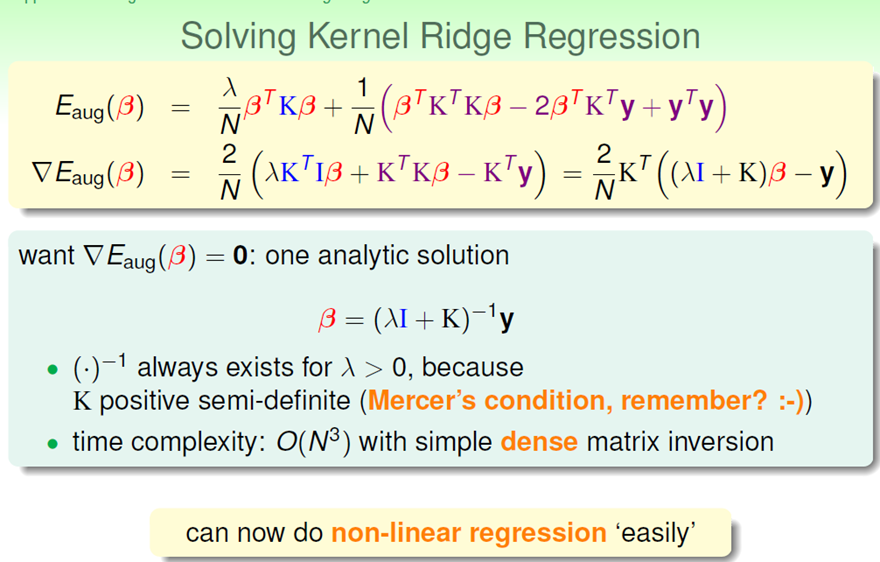
(一)kernel ridge regression
之前我们之前在做的是linear regression,现在我们希望在regression中使用kernel trick。
下面是linear versus kernel:
至此,kernel ridge regression结束。但是,这里的β与kernel logistic regression中的β存在同样的问题:β大多不是0。具体例子如下:
(二) support vector regression
前一篇文章中,有两个思路:1.把SVM与logistic regression混合起来用(先运行SVM,后运行logistic regression);2.将kernel trick加到logistic regression中;
这一次,我们已经完成了上述思路2:将kernel trick加到ridge regression中;却不打算完成上述的思路1了。
为什么不完成思路1了呢?一是因为课程中没有讲;二是把SVM与logistic regression混合起来得到的probabilistic SVM,我没有理解这一算法有什么好处。
我们现在希望:将kernel ridge regression中的β变得很sparse。这就要借助QP工具。
现在错误衡量方式为:
这种衡量方式得到的nonlinear error,跟SVM的nonlinear error 形式上很相似。所以可以使用SVM的求解方法。
形式上很相似。所以可以使用SVM的求解方法。
转化为SVM问题: