P1841 [JSOI2007]重要的城市
题目描述
参加jsoi冬令营的同学最近发现,由于南航校内修路截断了原来通向计算中心的路,导致去的路程比原先增加了近一公里。而食堂门前施工虽然也截断了原来通向计算中心的路,却没有使路程增加,因为可以找到同样长度的路作替代。其实,问题的关键在于,路截断的地方是交通要点。
同样的情况也出现在城市间的交通中。某些城市如果出了问题,可能会引起其他很多城市的交通不便。另一些城市则影响不到别的城市的交通。jsoi冬令营的同学发现这是一个有趣的问题,于是决定研究这个问题。
他们认为这样的城市是重要的:如果一个城市c被破坏后,存在两个不同的城市a和b(a, b均不等于c),a到b的最短距离增长了(或不通),则城市c是重要的。
jsoi冬令营的同学面对着一张教练组交给他们的城市间交通图,他们希望能找出所有重要的城市。现在就请你来解决这个问题。
输入输出格式
输入格式:
第一行两个整数N,M,N为城市数,M为道路数
接下来M行,每行三个整数,表示两个城市之间的无向边,以及之间的路的长度
输出格式:
一行,按递增次序输出若干的数,表示重要的城市。
Floyd好题。
一开始没读懂题意,感觉一眼傻逼题。直接枚举中间点判断就行了。
但是只有60分。
因为根据这个题的定义,如果存在这种情况:i到j之间有两条相等长度的最短路,那么这两条路上的所有点都不能被算为重要城市。
但是根据我一开始的做法,这些在某两个点之间的最短路上的点都是重要城市。
这里就有一个Floyd的知识了。
就是我们对于每一个点对,都会有一个中间点去更新这两个点的最短距离。
我一直对这个中转点的概念比较模糊,一直以为两个点之间有很多中转点。
但是ZAGER大佬给我讲说,可以很直观地发现,每一个点对最终都会只有唯一一个中转点。
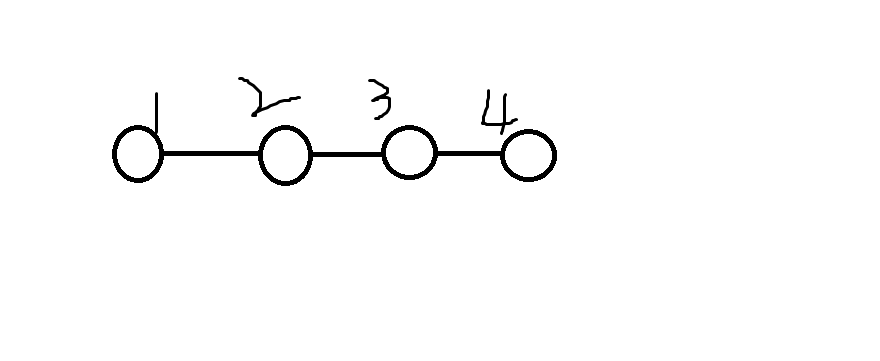
就像上图,1到4之间中转点只会是3,因为最后更新1到4的答案的是3,那么2呢?2会作为1到3的中转点。
所以对于这道题,我们只需要记录一下每个点对的中转点,如果有重复的,那么这些重复点都不是,没有的话,这些中转点就是答案中的点。
还是太菜了。。。
code:
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int wx=1107;
inline int read(){
int sum=0,f=1; char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9'){sum=(sum<<1)+(sum<<3)+ch-'0'; ch=getchar();}
return sum*f;
}
int n,m,tot;
int dis[wx][wx];
int ans[wx],mid[wx][wx];
int flag[wx][wx];
int main(){
n=read(); m=read();
memset(dis,0x3f,sizeof dis);
for(int i=1;i<=n;i++)dis[i][i]=0;
for(int i=1;i<=m;i++){
int x,y,z;
x=read(); y=read(); z=read();
dis[x][y]=dis[y][x]=min(z,dis[x][y]);
}
for(int k=1;k<=n;k++){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
// dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);
if(i!=j&&j!=k&&i!=k&&dis[i][j]>dis[i][k]+dis[k][j]){
dis[i][j]=dis[i][k]+dis[k][j];
mid[i][j]=mid[j][i]=k;
}
else if(dis[i][k]+dis[k][j]==dis[i][j]&&i!=j&&i!=k&&k!=j){
mid[i][j]=0;
}
}
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
ans[mid[i][j]]=1;
}
}
for(int i=1;i<=n;i++){
if(ans[i])printf("%d ",i),tot++;
}
if(!tot)puts("No important cities.");
return 0;
}