dijsktra求最短路径

讲算法原理的有很多，直接贴代码

dijkstra算法是直接对邻接矩阵进行操作求出最短路径的，我项目中的图结构需要转化成邻接矩阵，所以会有下面代码

图结构是一个map，first表示节点的index，second是一个结构体，包含节点的详细信息

map<int, node> routeTable;

struct node
{
public:  
   string ip;                //节点的ip
   int port;                 //节点的端口
   vector<OP_TYPE> ops;       //节点支持的OP
   float overload;            //节点的负载
   bool status;              // 节点的状态
   int ncmIndex;            //ncm index
   int reportCount;
   vector<pair<int,int>> adjacencyIndex; //邻接点的index及距离
};

所以需要根据这个map来生成一个邻接矩阵，dijkstra算法是从图的起点找出它与所有点的最短路径，而我的需求是给定两个点求他们在图上的最短距离，所以生成邻接矩阵不能按map本来的顺序去生成，需要将输入的两个点作为邻接矩阵的第一个点和最后一个点。举例来说如果原来节点的顺序是[0,1,2,3,4,5,6]，我们想求2和4在图上的最短距离，那么就需要将map便利的顺序变成[2,0,1,3,5,6,4]

生成邻接矩阵

std::vector<std::vector<int>> GlobalRouteTable::getRouteAdjacentMatrix(
    int startNodeIndex, int endNodeIndex)
{
    std::vector<int> graphNodeOrder = {};
    // 将startNodeIndex和endNodeIndex对应的点作为图遍历的起点和重点
    // if(routeTable.find(startNodeIndex)==routeTable.end()||routeTable.find(endNodeIndex)==routeTable.end())
    graphNodeOrder.push_back(startNodeIndex);
    for (auto it : routeTable) {
        if (it.first != startNodeIndex && it.first != endNodeIndex
            && it.second.adjacencyIndex[0].first != -1)
            graphNodeOrder.push_back(it.first);
    }
    graphNodeOrder.push_back(endNodeIndex);
    std::vector<std::vector<int>> adjacent_matrix;
    // 初始化邻接矩阵
    for (size_t i = 0; i < graphNodeOrder.size(); ++i) {
        std::vector<int> matrix_line = {};
        for (size_t j = 0; j < graphNodeOrder.size(); ++j)
            matrix_line.push_back(65535);
        adjacent_matrix.push_back(matrix_line);
    }
    // 对角线0
    for (size_t i = 0; i < graphNodeOrder.size(); ++i)
        adjacent_matrix[i][i] = 0;
    for (size_t i = 0; i < graphNodeOrder.size(); ++i) {
        for (auto j : routeTable[graphNodeOrder[i]].adjacencyIndex) {
            int tmp_index = 0;
            for (auto k = graphNodeOrder.begin(); k != graphNodeOrder.end();
                 ++k) {
                if (*k != j.first)
                    tmp_index += 1;
                else
                    break;
            }
            adjacent_matrix[i][tmp_index] = j.second;
        }
    }
    return adjacent_matrix;
}

求最短路径

int GlobalRouteTable::dijsktra(std::vector<std::vector<int>> &&graph_matrix)
{
    // init
    // 目标点到其他点的距离
    std::vector<int> dist = {};
    // 是否找到最短路径
    std::vector<bool> target = {};
    // 初始化图的第一个节点并录入与之相邻的节点的距离
    for (size_t i = 0; i < graph_matrix.size(); ++i) {
        dist.push_back(graph_matrix[0][i]);
        target.push_back(false);
    }
    target[0] = true;
    int min, k;
    // start search
    for (size_t i = 1; i < graph_matrix.size(); ++i) {
        min = 65535;
        for (size_t j = 1; j < graph_matrix.size(); ++j) {
            if (!target[j] && min > dist[j]) {
                min = dist[j];
                // 确定下一个要搜索的点
                k = j;
            }
        }
        target[k] = true;
        for (size_t j = 1; j < graph_matrix.size(); ++j) {
            if (!target[j] && dist[j] > dist[k] + graph_matrix[k][j]) {
                dist[j] = dist[k] + graph_matrix[k][j];
            }
        }
    }
    return dist[dist.size() - 1];
}

函数调用

int GlobalRouteTable::getNodeDist(int startNodeIndex, int endNodeIndex)
{
    if (startNodeIndex == endNodeIndex) return 0;
    return dijsktra(std::move(getRouteAdjacentMatrix(startNodeIndex, endNodeIndex)));
}

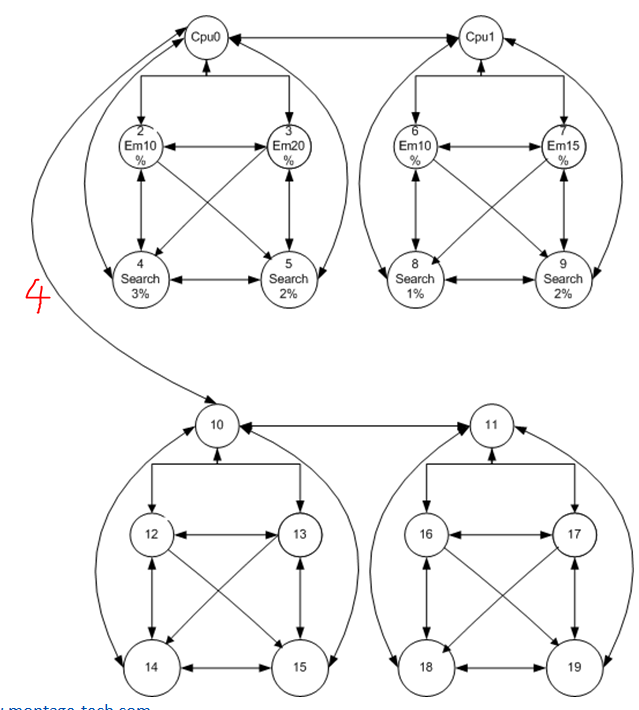
图结构

除了标记的变长是4，其余的边长都是1

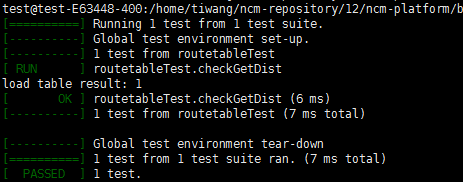
 测试用例

#include "../../src/routeTable.h"

#include <gtest/gtest.h>

TEST(routetableTest, checkGetDist)
{
    auto ptr = GlobalRouteTable::GetInstance();
    std::cout << "load table result: " << ptr->loadRouteTable() << std::endl;
    //
    ASSERT_EQ(ptr->getNodeDist(0, 0), 0);
    ASSERT_EQ(ptr->getNodeDist(0, 1), 1);
    ASSERT_EQ(ptr->getNodeDist(0, 2), 1);
    ASSERT_EQ(ptr->getNodeDist(2, 1), 2);
    ASSERT_EQ(ptr->getNodeDist(2, 3), 1);
    ASSERT_EQ(ptr->getNodeDist(2, 6), 3);
    ASSERT_EQ(ptr->getNodeDist(0, 10), 4);
    ASSERT_EQ(ptr->getNodeDist(0, 11), 5);
    ASSERT_EQ(ptr->getNodeDist(1, 11), 6);
    ASSERT_EQ(ptr->getNodeDist(0, 12), 5);
    ASSERT_EQ(ptr->getNodeDist(0, 16), 6);
    ASSERT_EQ(ptr->getNodeDist(2, 12), 6);
    ASSERT_EQ(ptr->getNodeDist(2, 16), 7);
    ASSERT_EQ(ptr->getNodeDist(6, 16), 8);
}
int main(int argc, char **argv)
{
    ::testing::InitGoogleTest(&argc, argv);
    return RUN_ALL_TESTS();
}