给定一个字符串s,找到其中最长的回文子序列。可以假设s的最大长度为1000。
示例 1:
输入:
"bbbab"
输出:
4
一个可能的最长回文子序列为 "bbbb"。
示例 2:
输入:
"cbbd"
输出:
2
一个可能的最长回文子序列为 "bb"。
解:
状态
f[i][j] 表示 s 的第 i 个字符到第 j 个字符组成的子串中,最长的回文序列长度是多少。
转移方程
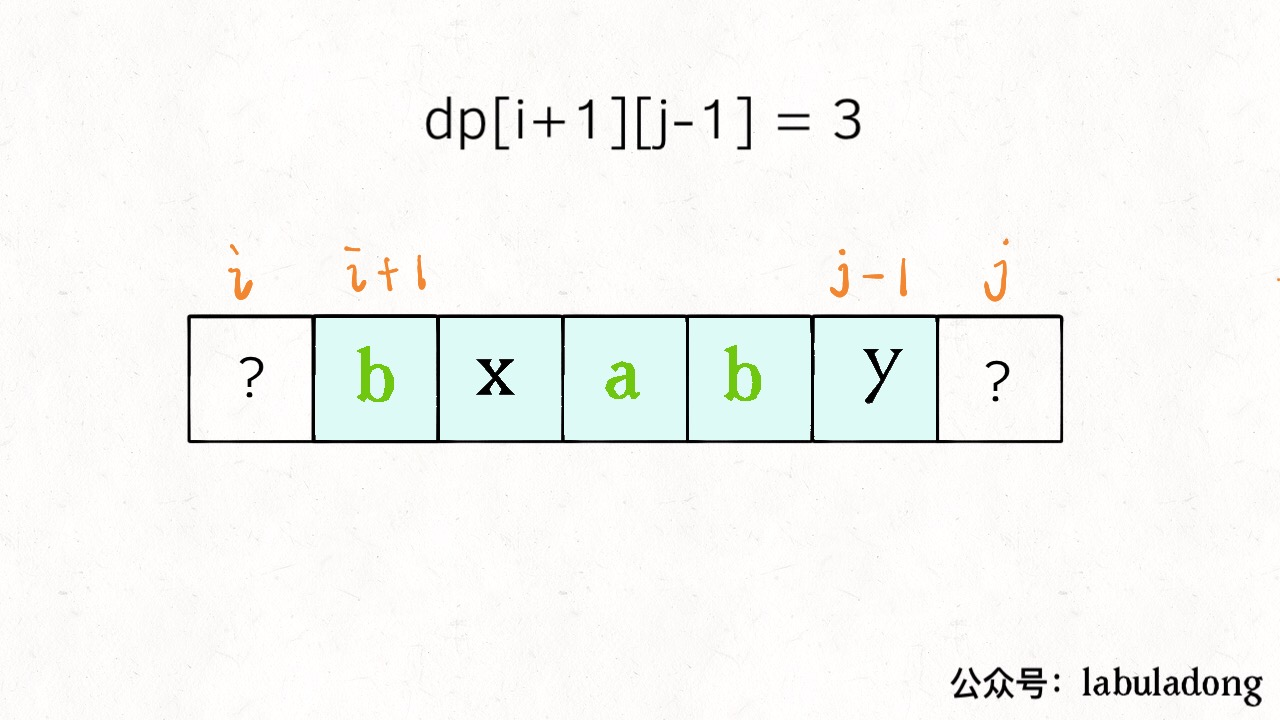
如果 s 的第 i 个字符和第 j 个字符相同的话
f[i][j] = f[i + 1][j - 1] + 2
如果 s 的第 i 个字符和第 j 个字符不同的话
f[i][j] = max(f[i + 1][j], f[i][j - 1])
然后注意遍历顺序,i 从最后一个字符开始往前遍历,j 从 i + 1 开始往后遍历,这样可以保证每个子问题都已经算好了。
初始化
f[i][i] = 1 单个字符的最长回文序列是 1
结果
f[0][n - 1]
用个别人的图
class Solution { public: int longestPalindromeSubseq(string s) { int n=s.size(); vector<vector<int>>dp(n,vector<int>(n,0)); //然后注意遍历顺序,i 从最后一个字符开始往前遍历,j 从 i + 1 开始往后遍历,这样可以保证每个子问题都已经算好了。 for(int i=n-1;i>=0;i--) { //每个数自己最小是1 dp[i][i]=1; for(int j=i+1;j<n;j++) { if(s[i]==s[j]) { dp[i][j]=dp[i+1][j-1]+2; } else { dp[i][j]=max(dp[i+1][j],dp[i][j-1]); } } } return dp[0][n-1]; } };