由4位同学参加由智力竞赛,竞赛规定:每人从甲、乙两类题中各随机选一题作答,且甲类题目答对得3分,答错扣3分;乙类题目答对得1分,答错扣1分。若每位同学答对与答错相互独立,且概率均为(cfrac{1}{2}),那么这4位同学得分之和为0的概率是多少?
说明:本题目的讲解需要排列组合知识的配合,对学生的要求比较高。
法1【互斥事件和相互独立事件】:
设4位同学为(A、B、C、D),每个人选甲和乙的概率也均为(cfrac{1}{2}),
所以每个人选择每个题目答对的概率是(cfrac{1}{4}),
比如(A)选甲题,答对概率(cfrac{1}{4}),答错概率(cfrac{1}{4}),(A)选乙题,答对概率(cfrac{1}{4}),答错概率(cfrac{1}{4}),
4个人的情形都是一样的。所以这4位同学得分之和为(0)的各种情形分类如下:
(1^。)全选甲题,得分(pm 3)成对出现,有(cfrac{A_4^4}{A_2^2A_2^2}=6)种可能;
即共有((3,-3,3,-3))、((3,3,-3,-3))、((3,-3,-3,3))、((-3,-3,3,3))、((-3,3,-3,3))、((-3,3,3,-3)),共有6种,
故概率为(3 imescfrac{1}{4} imescfrac{1}{4} imescfrac{1}{4} imescfrac{1}{4} imes2=cfrac{6}{256});
(2^。)全选乙题,得分(pm 1)成对出现,情形同上,有(cfrac{A_4^4}{A_2^2A_2^2}=6)种可能,概率为(cfrac{6}{256});
(3^。)选一个甲题,得分(3),选三个乙题,得分为(3)个(-1),
共有((3,-1,-1,-1))、((-1,3,-1,-1))、((-1,-1,3,-1))、((-1,-1,-1,3))共4种;
以及选一个甲题,得分(-3),选三个乙题,得分为(3)个(1),也有4种;有(2cfrac{A_4^4}{A_3^3}=8)种可能;
概率为(cfrac{4+4}{256}=cfrac{8}{256});
(4^。)选两个甲题,得分(pm 3)成对出现,选两个乙题,得分(pm 1)成对出现,
此时相当于4个元素做全排列,共有(A_4^4=24)种,故概率为(cfrac{24}{256});
以上各种情形彼此互斥,故所求概率为(cfrac{6+6+8+24}{256}=cfrac{44}{256}=cfrac{11}{64});
法2【排列组合法】:每人的得分情况均有4种(甲对,甲错,乙对,乙错)可能,因而总的情况有(4^4=256)种,若他们得分之和为0,则分为4类:
(1^。) 4人全选甲类题目且两对两错,有(cfrac{A_4^4}{A_2^2A_2^2}=6)种可能;(即就是四个元素(3,3,-3,-3)的所有排列个数)
(2^。) 4人全选乙类题目且两对两错,有(cfrac{A_4^4}{A_2^2A_2^2}=6)种可能;
(3^。) 4人中1人选甲类对或错,同时另3人选乙类全错或全对,有(2cfrac{A_4^4}{A_3^3}=8)种可能;
(4^。) 4人中2人选甲类一对一错,同时另2人选乙类一错一对,共有(A_4^4=24)种可能;
综上,所求概率为(cfrac{6+6+8+24}{256}=cfrac{44}{256}=cfrac{11}{64});
将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落过程中,将3次遇到黑色障碍物,最后落入(A)袋或(B)袋中.已知小球每次遇到黑色障碍物时向左、右两边下落的概率都是(cfrac{1}{2}).
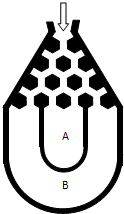
(Ⅰ)求小球落入(A、B)袋中的概率(P(A)、P(B));
(Ⅱ)在容器入口处依次放入3个小球,记(X)为落入(B)袋中小球的个数,试求(X)的分布列和数学期望(EX).
分析:(Ⅰ)设小球落入区域(A)为事件(A),小球落入区域(B)为事件(B),
由于小球落下不落入区域(A)必然会落入区域(B),故事件(A)和(B)互为对立事件;
要使小球每次落入区域(B)中,则小球必须每次都从左边落下,或者每次都从右边落下,
故(P(B)=cfrac{1}{2} imescfrac{1}{2} imescfrac{1}{2}+cfrac{1}{2} imescfrac{1}{2} imescfrac{1}{2}=cfrac{1}{4}),
由对立事件可知(P(A)=1-cfrac{1}{4}=cfrac{3}{4});
备注:如果从正面思考(P(A)=cfrac{3}{4}),可以仿照上例,
应该是6个(cfrac{1}{2} imescfrac{1}{2} imescfrac{1}{2}=cfrac{1}{8});故也有(P(A)=6 imes cfrac{1}{8}=cfrac{3}{4});
(Ⅱ)在容器入口处依次放入3个小球,每次小球落入区域(A)的概率都是(cfrac{3}{4}),相当于做了3次独立重复试验,
(X)为落入(A)袋中小球的个数,(X)的可能取值为(0,1,2,3),故(Xsim Bleft(3(n),cfrac{3}{4}(p) ight)),
(P(X=k)=C_3^k(cfrac{3}{4})^k(1-cfrac{3}{4})^{3-k},k=0,1,2,3),
即(P(X=0)=C_3^0(cfrac{3}{4})^0(1-cfrac{3}{4})^{3-0}=cfrac{1}{64});(P(X=1)=C_3^1(cfrac{3}{4})^1(1-cfrac{3}{4})^{3-1}=cfrac{9}{64});
(P(X=2)=C_3^2(cfrac{3}{4})^2(1-cfrac{3}{4})^{3-2}=cfrac{27}{64});(P(X=3)=C_3^3(cfrac{3}{4})^3(1-cfrac{3}{4})^{3-3}=cfrac{27}{64});
故(X)的分布列为
| (X(X=k)) | (0) | (1) | (2) | (3) |
|---|---|---|---|---|
| (P(X=k)) | (cfrac{1}{64}) | (cfrac{9}{64}) | (cfrac{27}{64}) | (cfrac{27}{64}) |
数学期望$EX=np=3 imescfrac{3}{4}=cfrac{9}{4} $.
或$EX=0 imescfrac{1}{64}+1 imescfrac{9}{64}+2 imescfrac{27}{64}+3 imescfrac{27}{64}=cfrac{9}{4} $.
将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落过程中,将3次遇到黑色障碍物,最后落入(A)袋或(B)袋中.已知小球每次遇到黑色障碍物时向左、右两边下落的概率分别是(cfrac{1}{3}和cfrac{2}{3}).

(Ⅰ)求小球落入(A、B)袋中的概率(P(A)、P(B));
(Ⅱ)在容器入口处依次放入4个小球,记(X)为落入(B)袋中小球的个数,试求(X)的分布列和数学期望(EX).
分析:(Ⅰ)设小球落入区域(A)为事件(A),小球落入区域(B)为事件(B),
由于小球落下不落入区域(A)必然会落入区域(B),故事件(A)和(B)互为对立事件;
要使小球每次落入区域(B)中,则小球必须每次都从左边落下,或者每次都从右边落下,
故(P(B)=cfrac{1}{3} imescfrac{1}{3} imescfrac{1}{3}+cfrac{2}{3} imescfrac{2}{3} imescfrac{2}{3}=cfrac{1}{3}),
由对立事件可知(P(A)=1-cfrac{1}{3}=cfrac{2}{3});
备注:如果从正面思考(P(A)=cfrac{2}{3}),可以仿照上例,
应该是以下的六种情形:
(cfrac{1}{3} imescfrac{1}{3} imescfrac{2}{3});(cfrac{1}{3} imescfrac{1}{3} imescfrac{2}{3});
(cfrac{1}{3} imescfrac{2}{3} imescfrac{1}{3});(cfrac{2}{3} imescfrac{2}{3} imescfrac{1}{3});
(cfrac{2}{3} imescfrac{1}{3} imescfrac{2}{3});(cfrac{2}{3} imescfrac{1}{3} imescfrac{1}{3});
其和为(cfrac{18}{27}=cfrac{2}{3}).
(Ⅱ)在容器入口处依次放入4个小球,每次小球落入区域(A)的概率都是(cfrac{2}{3}),相当于做了4次独立重复试验,
(X)为落入(A)袋中小球的个数,(X)的可能取值为(0,1,2,3,4),故(Xsim Bleft(4,cfrac{2}{3} ight)),
(P(X=k)=C_4^k(cfrac{2}{3})^k(1-cfrac{2}{3})^{4-k},k=0,1,2,3,4),
数学期望$EX=4 imescfrac{2}{3}=cfrac{8}{3} $.
甲乙两人轮流投篮,每人每次投篮一次,先投中者获胜。投篮进行到有人获胜或每人都已经投球3次时结束。设甲每次投篮命中的概率为(cfrac{2}{5}),乙每次投篮命中的概率为(cfrac{2}{3}),且各次投篮互不影响,现由甲先投。
⑴求甲获胜的概率;
⑵求投篮结束时甲的投篮次数(X)的分布列和数学期望。
分析:⑴
| 甲 | 乙 | 甲 | 乙 | 甲 | 乙 |
|---|---|---|---|---|---|
| Y | Y | Y | Y | Y | Y |
| N | N | N | N | N | N |
由表格可以看出,甲获胜有这些事件:
(A_1:)一次投中;(A_2:)前两次甲乙都未投中,第三次甲投中;
(A_3:)前四次甲乙都未投中,第五次甲投中;
这些事件彼此互斥,甲获胜的事件为(A_1+A_2+A_3)
且(P(A_1)=cfrac{2}{5}),(P(A_2)=cfrac{3}{5} imes cfrac{1}{3} imescfrac{2}{5}=cfrac{2}{25}) ,
(P(A_3)=cfrac{3}{5} imes cfrac{1}{3} imescfrac{3}{5} imes cfrac{1}{3} imescfrac{2}{5}=cfrac{2}{125}) ,
所以(P(A_1+A_2+A_3)=cfrac{2}{5}+cfrac{2}{25}+cfrac{2}{125}=cfrac{62}{125});
⑵(X)的所有可能取值为(1,2,3).
(X=1)包含甲投篮一次命中和甲第一次未命中而乙命中,(P(X=1)=cfrac{2}{5}+cfrac{3}{5} imescfrac{2}{3}=cfrac{4}{5});
(X=2)包含前两次甲乙未命中而第三次甲投中和前三次甲乙未命中而第四次乙命中,(P(X=2)=cfrac{3}{5} imescfrac{1}{3} imescfrac{2}{5}+cfrac{3}{5} imescfrac{1}{3} imescfrac{3}{5} imescfrac{2}{3}=cfrac{4}{25});
(X=3)包含前四次甲乙未命中而第五次甲投中和前五次甲乙未命中而第六次乙命中和六次投篮两人都未投中导致结束,
(P(X=3)=cfrac{3}{5} imescfrac{1}{3} imescfrac{3}{5} imescfrac{1}{3} imescfrac{2}{5})
(+cfrac{3}{5} imescfrac{1}{3} imescfrac{3}{5} imescfrac{1}{3} imescfrac{3}{5} imescfrac{2}{3})
(+cfrac{3}{5} imescfrac{1}{3} imescfrac{3}{5} imescfrac{1}{3} imescfrac{3}{5} imescfrac{1}{3})
(=cfrac{1}{25});
分布列略;故数学期望为(E(X)=1 imescfrac{4}{5}+2 imescfrac{4}{25}+3 imescfrac{1}{25}=cfrac{31}{25}).
某品牌汽车4S店,对最近100例分期付款购车情况进行统计得到下表。该店经销一辆该品牌汽车,若顾客分3期付款,其利润为1万元;若顾客分6期或9期付款,其利润为2万元;若顾客分12期付款,其利润为3万元;
| 付款方式 | 分3期 | 分6期 | 分9期 | 分12期 |
|---|---|---|---|---|
| 频数 | 20 | 20 | 40 | 20 |
⑴若以表中计算出的频率近似替代概率,从该店采用分期付款购车的顾客(数量较大)中随机抽取3名顾客,求事件(A):“至多有1位采用分6期付款”的概率(P(A))
⑵按分层抽样的方式从这100位顾客中抽取5位人,再从抽取的5人中随机抽取3人,记该店在这3人身上赚取的总利润为随机变量(eta),求(eta)的分布列和数学期望(E(eta))
解析:⑴由题目可知令付款的期数为(zeta),则(P(zeta=3)=cfrac{1}{5});(P(zeta=6)=cfrac{1}{5});(P(zeta=9)=cfrac{2}{5});(P(zeta=12)=cfrac{1}{5});由于题目中问的涉及分6期付款的人数,故
分6期付款的概率为(cfrac{1}{5}),其他的付款都可以归到未分6期付款中去,概率为(cfrac{4}{5}),再令(X)为分6期付款的人数,则(X=0,1,2,3),容易知道(Xsim (3,cfrac{1}{5})),事件(A)则对应(X=0)和(X=1),故(P(A)=P(X=0)+P(X=1)=C_3^0(cfrac{1}{5})^0(cfrac{4}{5})^3+C_3^1(cfrac{1}{5})^1(cfrac{4}{5})^2=cfrac{64}{125}+cfrac{48}{125}=cfrac{112}{125})
⑵用分层抽样的方式从分期3、6、9、12期的人中,分别抽出的人数是1个(记为(A),利润为1万)、1个(记为(B),利润为2万)、2个(记为(CC),利润为2万)、1个(记为(D),利润为3万),
再从这5人中抽出三个,共有以下不同情形:(ABC,eta=5);(ABD,eta=6);(ACD,eta=6);(ACC,eta=5);(BCD,eta=7);(BCC,eta=6);(CCD,eta=7);再写出对应的概率
(P(eta=5)=cfrac{C_1^1C_1^1C_2^1+C_1^1C_2^2}{C_5^3}=cfrac{3}{10});(P(eta=6)=cfrac{C_1^1C_1^1C_1^1+C_1^1C_2^1C_1^1+C_1^1C_2^2}{C_5^3}=cfrac{4}{10});(P(eta=7)=cfrac{C_1^1C_1^1C_2^1+C_1^1C_2^2}{C_5^3}=cfrac{3}{10});
分布列略,故数学期望(E(eta)=5 imescfrac{3}{10}+6 imescfrac{4}{10}+7 imescfrac{3}{10}=6(万))。
(n)是一个三位正整数,且(n)的个位数字大于十位数字,十位数字大于百位数字,则称(n)为“三位递增数”(如(137),(358),(567)等)。在某次活动中,每位参加者需从所有的“三位递增数”中随机抽取1个数,且只能抽取一次。得分规则如下:若抽取的“三位递增数”的三个数字之积不能被5整除,得分0分;若能被5整除,但不能被10整除,得分-1分;若能被10整除,得分1分。
(1).写出所有个位数字是5的“三位递增数”。
分析:按照一定的次序列举即可,有125,135,145;235, 245;345;共有6个。
(2).若甲参加活动,求甲得分(X)的分布列和数学期望(EX)。
分析:所有的“三位递增数”共有(C_9^3)个,其中(X)的所有可能取值为0,1,-1.
(X=0)对应所取的数字中不含有5,故从剩余的8个数字中任取3个,故(P(X=0)=cfrac{C_8^3}{C_9^3}=cfrac{2}{3});
(X=-1)对应所取的数字中含有5,但是不能包含4个偶数,故(P(X=-1)=cfrac{C_4^2C_1^1}{C_9^3}=cfrac{2}{3}=cfrac{1}{14});
(X=1)对应所取的数字中含有5,且必须至少含有1个偶数,故(P(X=1)=cfrac{C_4^1C_4^1C_1^1+C_1^1C_4^2}{C_9^3}=cfrac{11}{42});
分布列略,数学期望(EX=0 imescfrac{2}{3}+(-1) imescfrac{1}{14}+1 imescfrac{11}{42}=cfrac{4}{21})。
反思总结:
1、只能从1-9这9个数字中选取,每次任取3个数字,比如3,2,7,只能构成一个“三位递增数”。
2、(X=1)的情形包含(5+奇+偶)和(5+偶+偶)两种情况。