前言
案例研究
- 正方体截面的探究
【目的】结合正方体截面设计的问题串,引导学生完成探究、发现、证明新问题的过程,积累数学探究的经验。
【情境】用一个平面截正方体,截面的形状将会是什么样的?启发学生提出逐渐深入的系列问题,引导学生进行逐渐深刻的思考。
学生可以自主或在教师引导下提出一些问题,例如:
(1)给出截面图形的分类原则,找到截得这些形状截面的方法,面出这些截面的示意图。
例如,可以按照截面图形的边数进行分类,比如三角形,四边形,五边形,六边形等等。
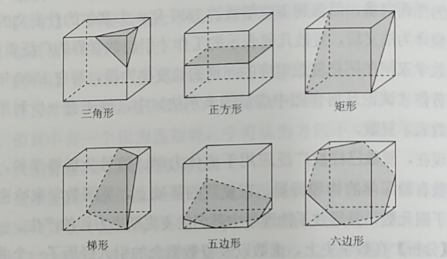
(2)如果截面是三角形,可以截出几类不同的三角形?为什么?
(3)如果截面是四边形,可以截出几类不同的四边形?为什么?
(4)还能截出哪些多边形?为什么?然后进一步探讨:
(5)能否截出正五边形?为什么?
(6)能否截出直角三角形?为什么?
(7)有没有可能截出边数超过6的多边形?为什么?
(8)是否存在正六边形的截面?为什么?
最后思考:
(9)截面面积最大的三角形是什么形状的三角形?为什么?
【分析】这是一个跨度很大的数学问题串,可以针对不同学生,设计不同的教学方式,通过多种方法实施探究。例如,
①可以通过切萝卜块观察,启发思路;
②也可以在透明的正方体盒子中注入有颜色的水,观察不同摆放位置、不同水量时的液体表面的形状;
还可以借助信息技术直观快捷地展示各种可能的截面。
但是,观察不能代替证明。探究的难点是分类找出所有可能的截面,并证明哪些形状的截面一定存在或者一定不存在。可以鼓励学生通过操作观察,形成猜想,证现最证。龙这样逐渐深入的探究过程,有利于培养学生8问题、分类讨论、作图表达、推理论证等能力,在具体情做事限升直观想象、数学抽象、逻辑推理等素养,积累教学探的洋么、
典例剖析

①当 (x=0) 时, (S) 为矩形,其面积最大为 (1);
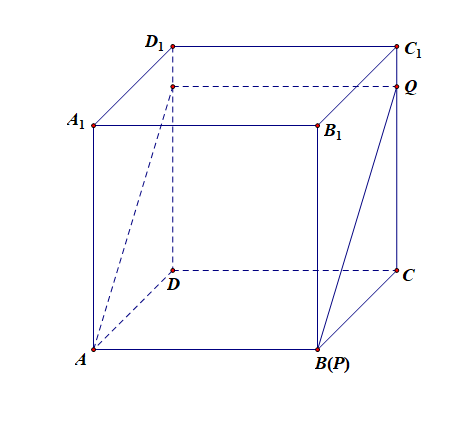
分析:当 (x=0) 时, (S) 为矩形,其面积最大时为矩形(ABC_1D_1),故最大面积为(sqrt{2}),故①错误;
②当 (x=y=cfrac{1}{2}) 时, (S) 为等腰梯形;

分析:如上图,由于(x=y=cfrac{1}{2}),容易证明(AP=D_1Q),而(PQ//AD_1),故截面(S) 为等腰梯形;故②正确;
③当 (x=cfrac{1}{2}),(yin(cfrac{1}{2}, 1)) 时, 设 (S) 与棱 (C_{1}D_{1}) 的交点为 (R),则 (RD_{1}=2-cfrac{1}{y});
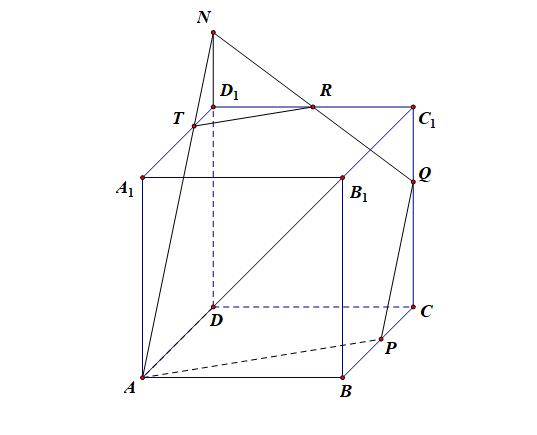
分析:设 (S) 与棱 (C_{1}D_{1}) 的交点为 (R),延长(DD_1),使(DD_1cap QR=N),
连接(AN)交(A_1D_1)于(T),连接(TR),可证(AN//PQ)一个平面和两个平行平面都相交,则所得的交线互相平行;(quad),
故可知( riangle PCQsim riangle AD_1N),则(cfrac{PC}{AD}=cfrac{CQ}{DN}=cfrac{1}{2}),
即(cfrac{y}{DN}=cfrac{1}{2}),故(DN=2y),则(D_1N=2y-1);
又由于( riangle NRD_1sim riangle QRC_1),可得(cfrac{C_1R}{D_1R}=cfrac{C_1Q}{D_1N}),
令(RD_1=x),即(cfrac{1-x}{x}=cfrac{1-y}{2y-1}),利用合比定理,得到
(cfrac{1-x+x}{x}=cfrac{1-y+2y-1}{2y-1}),即(cfrac{1}{x}=cfrac{y}{2y-1})
可得(x=RD_1=2-cfrac{1}{y}),故③正确;
④当 (y=1) 时, 以 (B_1)为顶点,(S) 为底面的棱锥的体积为定值(cfrac{1}{3}); 其中正确的命题为_______________.

分析:当 (y=1) 时, 以 (B_1)为顶点,(S) 为底面的棱锥(B_1-PC_1MA)的体积为
(V_{B_1-PC_1MA}=2V_{B_1-PC_1M}=2V_{P-B_1C_1M}=2 imescfrac{1}{3} imescfrac{1}{2} imes 1 imes 1 imes 1=cfrac{1}{3}),故④正确;
综上所述,正确的命题为②③④;