前言
熟练掌握形如(y=2sin(2x+cfrac{pi}{6})+1,xin[0,cfrac{pi}{2}])的值域的快速求解方法。
典例剖析
【错误解法】:初学三角函数的高中学生,最常见的错误解法如下:
当(x=0)时,(y=2sin(2 imes 0+cfrac{pi}{6})+1=2),
当(x=cfrac{pi}{2})时,(y=2sin(2 imes cfrac{pi}{2}+cfrac{pi}{6})+1=0),
所以,所求的值域为([0,2]);
[错因分析]:上述的解法,仅仅适用于函数在(xin[0,cfrac{pi}{2}])上单调递增的情形的值域的求解思路和方法,但是我们碰到的绝大多数三角函数在给定的区间上往往都不是单调函数,故利用求端点值的方法往往是错误的。
正确解法1:横轴为(x),如图1所示,利用图像的变换得到函数(y=2sin(2x+cfrac{pi}{6})+1,xin[0,cfrac{pi}{2}])的图像,
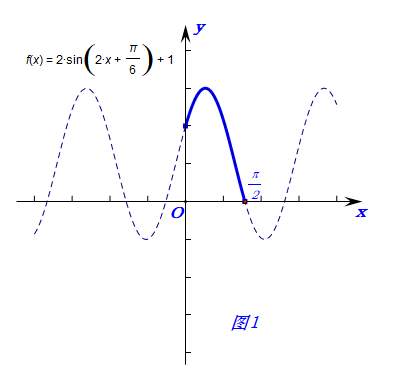
由图像可以看出来,当(x=cfrac{pi}{2})时,函数(f(x)_{min}=2sin(2 imescfrac{pi}{2}+cfrac{pi}{6})+1=0),
当(x=cfrac{pi}{6})时,函数(f(x)_{max}=2sin(2 imescfrac{pi}{6}+cfrac{pi}{6})+1=3),
故函数的值域为([0,3])。
快速解法2:整体代换,如图2所示,横轴为(2x+cfrac{pi}{6}=X),
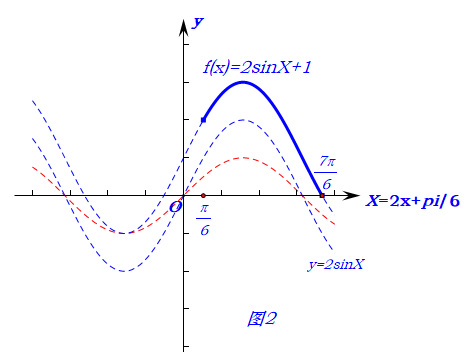
由(0leq xleq cfrac{pi}{2}),
故(cfrac{pi}{6}leq 2x+cfrac{pi}{6}leq cfrac{7pi}{6}),
则(-cfrac{1}{2}leq sin(2x+cfrac{pi}{6})leq 1),
则(0leq 2sin(2x+cfrac{pi}{6})+1leq 3),
故(0leq yleq 3)。
反思总结:
1、从作图角度讲,图2的做法由于使用了整体代换,作图过程简单明了,思路清晰,截取快捷,故常用图2的方法来做三角函数的图像。
2、用图2的方法也可以求解函数的单调区间。比如,对函数(y=2sinX+1)而言,在(Xin [cfrac{pi}{6},cfrac{pi}{2}])上单调递增,即(2x+cfrac{pi}{6}in [cfrac{pi}{6},cfrac{pi}{2}])上单调递增,解得(xin [0,cfrac{pi}{6}]),即函数(y=2sin(2x+cfrac{pi}{6})+1)在区间([0,cfrac{pi}{6}])上单调递增,和图1的单调递增区间是一样的。
值域妙用
我们都知道,(sin xin [-1,1]),(cos xin [-1,1]),但是很少能将其和导数主动融合在一起。
比如,函数(f(x)=sin x+x),在判断函数的单调性时,许多学生会想到用两个函数的图像叠合的方法求解,其实这个思路是错误的,(y=x)是单调递增的,但是(y=sin x)是有增有减的,故使用这个方法是说不清楚的;
换个思路,(f'(x)=1+cos x),那么由于(cos xin [-1,1]),则(1+cos xin [0,2]),
故能很容易得到,(f'(x)geqslant 0)恒成立,故函数(f(x)=sin x+x)在((-infty,+infty))上是单调递增的;
常见函数
(f(x)=xpm sin x),则(f'(x)geqslant 0);故函数(f(x))在((-infty,+infty))上是单调递增的;
(f(x)=xpm cos x),则(f'(x)geqslant 0);故函数(f(x))在((-infty,+infty))上是单调递增的;
(f(x)=3xpm 2sin x),则(f'(x)geqslant 0);故函数(f(x))在((-infty,+infty))上是单调递增的;