判断三角形个数

前言

利用正余弦定理判断三角形的个数的常用思路：

①代数法：从数的角度思考，根据大边对大角的性质，三角形内角和公式，正弦函数值判断；

②几何图形法，从形的角度思考，根据条件画出图形，通过图形直观判断三角形的个数；

情形列举

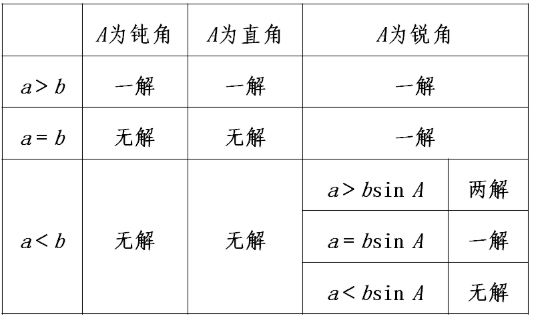
在( riangle ABC)中，已知(a，b，A)，三角形的解的个数比较复杂，见下表

典例剖析

例1在( riangle ABC)中，已知(a=2)，(b=sqrt{6})，(angle A=45^{circ})，则满足条件的三角形有【】个。

$A.1$ $B.2$ $C.0$ $D.无法确定$

法1：代数法，由(cfrac{a}{sinA}=cfrac{b}{sinB})，得到(sinB=cfrac{sqrt{3}}{2})，

故(B=60^{circ})或(B=120^{circ})，则对应的三角形有两个，故选(B)；

法2：几何图形法，可仿例3完成，由于(bsinA=sqrt{3})，则(bsinA<a<b)，

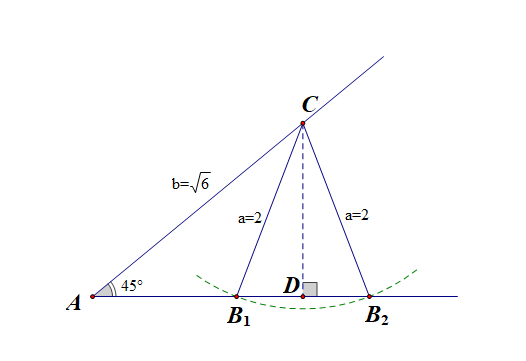
故满足条件的三角形有两个。

例2在(Delta ABC)中，已知(b=40)，(c=20)，(angle C=60^{circ})，则此三角形(Delta ABC)的解的情况是如何的？

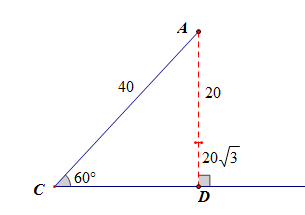
法1：从形的角度，如图所示，(AD=20sqrt{3})，当以点(A)为圆心，以(20)为半径做圆时，

此时和角的另一边(CD)没有交点，故满足题意的三角形是不存在的。

法2：从数的角度，如果这样的三角形是存在的，那么由正弦定理可知，

(cfrac{b}{sinB}=cfrac{c}{sinC})，得到(sinB=cfrac{bsinC}{c}=sqrt{3}>1)，

我们知道(|sinx|leq 1)，故这样的(B)不存在，即满足题意的三角形不存在。

例3如果(angle ABC=60^{circ})，(BC=12)，(AC=k)，则所构成的三角形(Delta ABC)的个数是如何随(k)变化的？

分析：这样的题目我们一般是从形的角度入手分析的多见一些，因为毕竟有形的帮助要直观的多。

如图所示，由图像可知(CD=6sqrt{3})，

当(kin(0，6sqrt{3}))时，满足题意的三角形不存在；

当(k=6sqrt{3})时，满足题意的三角形是唯一的，且是直角三角形。

当(kin(6sqrt{3}，12))时，满足题意的三角形是两个。

当(k=12)时，满足题意的三角形是一个，是等腰三角形。

当(k>12)时，满足题意的三角形是一个。

【解后反思】1、学生对这类题目的掌握一般都不太好，不会作图，不会应用图像解决问题。

2、这类题目作图的顺序是这样的，先做出(angle B)，一条已知边(BC)要么水平放置，要么斜放着，一般都是斜放着，此时点(C)就有了着落，这样放置也便于求点(C)到下底边上的高，然后以点(C)为圆心，以(AC)长为半径画弧，若所画的弧与下底边有交点，这个交点就是点(A)，有几个交点就意味着有几个三角形存在，若所画的弧与下底边没有交点，则这样的三角形是不存在的。

例4如果满足(angle ABC=60^{circ})，(AC=12)，(BC=k)的三角形(Delta ABC)恰有一个，那么(k)的范围是多少？

法1：从数的角度入手，由正弦定理(cfrac{k}{sinA}=cfrac{12}{sin60^{circ}})，

得到方程(k=8sqrt{3}sinA，Ain(0，cfrac{2pi}{3}))有一个解，或者两个函数图像有一个交点，数形结合求解即可。

由图可知，满足题意的三角形恰有一个，则(kin(0，12])或(k=8sqrt{3})。

法2：从形的角度入手，动静元素互相换位，即理解为让长度为(12)的边变化，让长度为(k)的边不变化。

如图，以点(C)为圆心画弧，当(12)小于点(C)到边(AB)的高度(k imescfrac{sqrt{3}}{2})时，

即(k imescfrac{sqrt{3}}{2}>12)时，解得(k>8sqrt{3})，此时三角形是不存在的；

当(12)等于点(C)到边(AB)的高度(k imescfrac{sqrt{3}}{2})时，

即(12=kcfrac{sqrt{3}}{2})，解得(k=8sqrt{3})，三角形是唯一的；

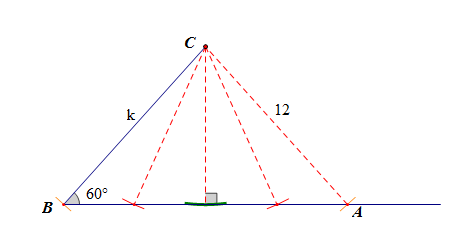
当(12)大于点(C)到边(AB)的高度(kcdotcfrac{sqrt{3}}{2})时，三角形是两个的，

即(12>k imes cfrac{sqrt{3}}{2})，解得(k<8sqrt{3})；

当(12)大于或等于边(BC)时，三角形是唯一的，即(0<kleqslant 12)，

综上可知，当(k=8sqrt{3})或(kin(0，12])时，满足条件的三角形恰好只有一个。

【解后反思】①动静互换，体现了思维的灵活性；②是否可以这样想，有一种从形入手分析的思路，必然就会有一种从数入手的思路与之对应。