函数图像的辨析

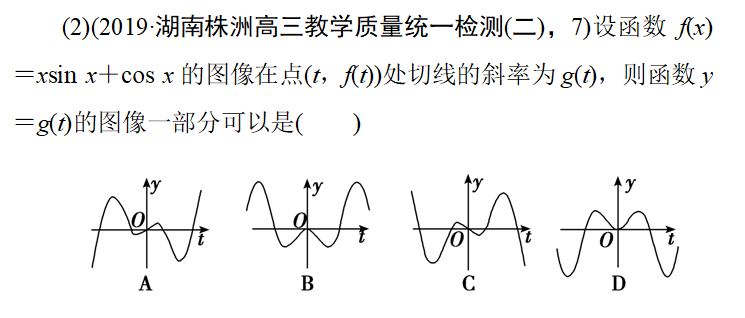
前言

函数图像的识别、辨析问题，常考查函数的奇偶性，函数值的正负、单调性、对称性、零点、极限、极值等，常用排除法；其一般的步骤是：定义域；值域；周期性；奇偶性；确定单调区间，极值点等；求函数的某些特殊点，如与坐标轴的交点，不连续点；考察渐近线；

解题思路

①由函数的定义域判断图像的左、右位置；

②由函数的定义域判断图像的上、下位置；

③由函数的单调性判断图像的变化趋势；

④由函数的奇偶性判断图像的对称性；

⑤由函数的周期性判断图像的循环往复；

奇偶函数

• 常见的奇函数：

$f(x)=kx$；

$f(x)=x^3$；

$f(x)=x^k(k为奇数)$；

$y=Asinomega x$；

$y=e^x-e^{-x}$；

$y=2^x-2^{-x}$；

$y=lnfrac{x+1}{x-1}$；

$f(x)=x+frac{k}{x}(k eq 0)$；

$g(x)=lg(sqrt{sin^2x+1}+sinx)$；

$g(x)=x^3+lg(sqrt{x^2+1}+x)$；

$f(x)=x^3pm 3sinx$

$f(x)=ln(sqrt{x^2+1}-x)$；

$g(x)=cfrac{2^x-1}{2^x+1}$；

$f(x)=cfrac{2^x+1}{2^x-1}$

备注：(g(-x)=cfrac{2^{-x}-1}{2^{-x}+1}=cfrac{(2^{-x}-1)cdot 2^x}{(2^{-x}+1)cdot 2^x}=cfrac{1-2^{x}}{2^{x}+1}=-g(x))

• 常见的偶函数：

$f(x)=x^2$；

$y=k|x|(kin R)$；

$y=e^{|x|}$；

$f(x)=x^k(k为偶数)$；

$y=Acos omega x+k$；

$y=e^x+e^{-x}$；

$y=2^x+2^{-x}$；

$f(x)=ln(1+|x|)$；

$f(x)=frac{|x|}{x^2+1}$

$h(x)=ln(2^x+2^{-x})$；

典例剖析

例1【2019高三理科数学启动卷，2019陕西省二检试卷第7题】已知函数(f(x)=x^2-e^{|x-1|}-2x+3)，则(f(x))的大致图像是【】

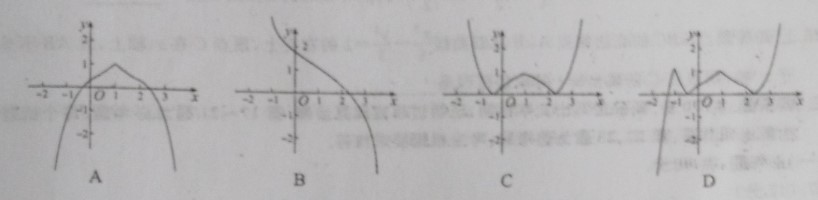
分析：为求作函数(f(x)=x^2-e^{|x-1|}-2x+3=(x-1)^2-e^{|x-1|}+2)的图像，选函数(g(x)=x^2-e^{|x|}+2)为模板函数，偶函数，故函数(f(x))的图像关于直线(x=1)对称，故排除(B)和(D)，再用赋值法，(f(3)=3^2-e^2-6+3<0)，则排除(C)，故选(D)。

例2【2019高三理科数学三轮模拟试题】已知函数(f(x)=e^{|x|}cdot cosx)，则(f(x))的大致图像是【】

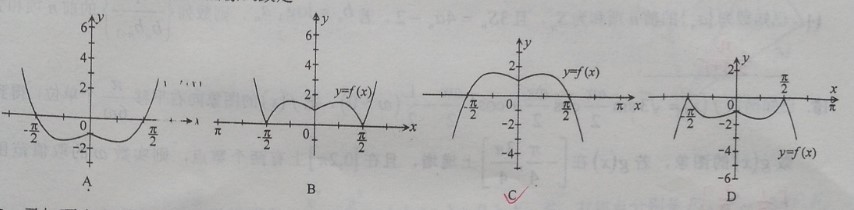
分析：函数(f(x))为偶函数，结合赋值法，选(C).

例3

提示：选(B).

例4