文章知识点来至于大话数据结构里边章节知识, 这篇主要介绍查找功能在计算机中存储形式, 以及在某些算法领域中对图的相关应用。本篇涉及到的知识点也比较多在查找中介绍了线性查找、折半查找、二叉排序树。该篇主要以二叉排序树为例,通过流程图以及算法实现来掌握二叉排序树的增删改查功能。相关代码源码请查看文章最后。本篇最后的算法描述和流程图以及代码实现是重点,如果对本篇感兴趣一定要通过该部分来巩固数据机构。
查找
查找就是根据给定的某个值,在查找表中确定一个其关键字等于给定值的数据元素。
1 顺序表查找
定义:又叫线性查找,是最基本的查找技术,它的查找过程是:从表中第一个(或最后一个)记录开始,逐个进行关键之与给定值比较,若某个记录的关键字和给定值相等,则查找成功,找到所查的记录;如果知道最后一个记录,其关键字与给定值比较都不等时,则表中没有所查找的记录,查找不成功。
2 有序表查找
折半查找:又称二分查找。它的前提是线性表中的记录必须是关键码有序的(通常是从小到大有序),线性表必须采用顺序存储。
插值查找:是根据要查找的关键字key与查找表中最大最小记录的关键字比较后的查找方法,其核心就在于插值的计算公式: 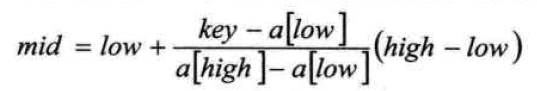
线性索引查找:索引就是把一个关键字与他对应的记录想关联的过程。索引按照结构可以分为:线性索引、树形索引、多级索引。所谓线性索引就是将索引项集合组织为线性表,也称为索引表。常见线性索引包括:稠密索引、分块索引、倒排索引。
(1)稠密索引:是指在线性索引,将数据集中的每个记录对应一个索引项。
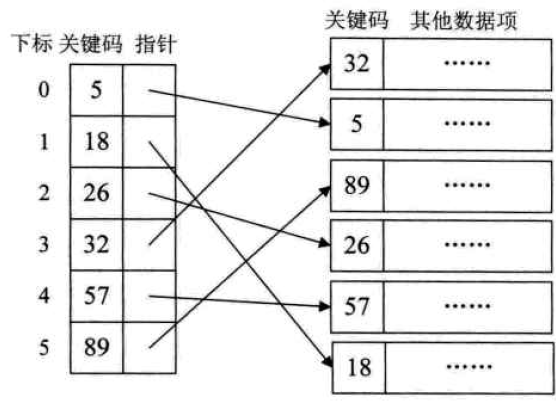
缺点:如果数据量非常大,上亿条。那么索引也得同样的数据集长度规模。
(2) 分块索引(关系型数据库使用):特点是分块有序,是把数据集的记录分成了若干块,并且这些块需要满足两个条件:
*块内无序,即每个块内不要求有序;
*块间有序,例如第二块的所有记录的关键字均要大于第一块中的所以记录的关键字。
对于分块有序的数据集,将每块对应一个索引项,这种索引方法叫做分块索引。索引项机构分为三个数据项:
*最大关键码,存储每一块中最大的关键字;
*存储了每块的记录数,以便于循环使用;
*用于指向块首数据元素的指针;
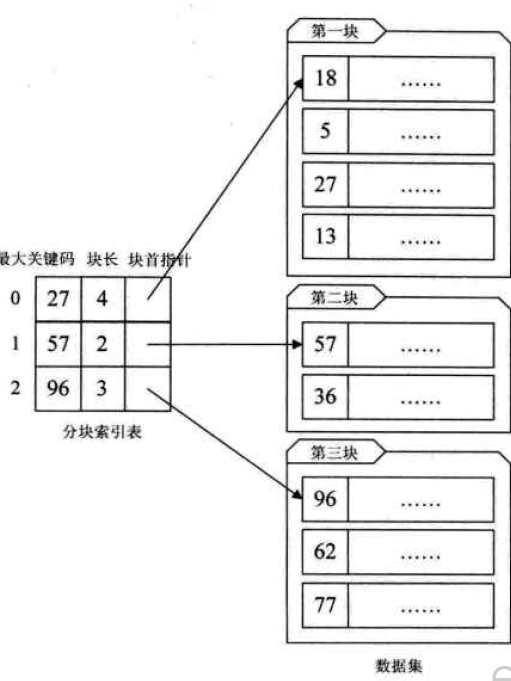
(3)倒排索引(搜索引擎使用):首先看图,图表示单词以及档次在哪些文章中出现。这张单词表就是索引表. 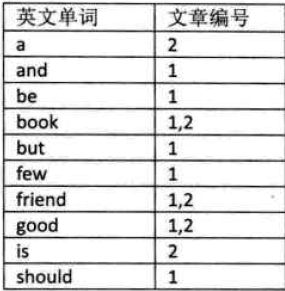
索引项的通用结构:
其中记录号表存储具有相同次关键字的所有记录的记录号(可以是指向记录的指针或者是该记录的主关键字)。这样的索引方法就是倒排序索引。
3 二叉排序树
定义:二叉排序树(Binary Sort Tree),又称为二叉查找树。它或者是一颗空树,或者是具有下列性质的二叉树。
若它的左子树不空,则左子树上所有的节点的值均小于根节点值;
若它的右子树不空,则右子树所有的节点的值均大于根节点值;
它的左、右子树也分别为二叉排序树
二叉排序树查找方法



二叉排序树插入方法


二叉排序树删除方法


二叉排序树优点
二叉排序树是以连接的方式存储,保持了连接存储结构在执行插入或删除操作时不用移动元素的优点,只要找到合适的插入或删除位置后,仅需修改连接指针即可。插入和删除的事件性能比较好。
4 平衡二叉树(AVL树)
定义:平衡二叉树是一种二叉排序树,其中每一个节点的的左子树和右子树的高度差之多等于1。我们将二叉树上结点的左子树深度减去右子树深度的值称为平衡因子BF(Balance Factor)。
最小不平衡子树:距离插入节点最近的,且平衡因子的绝对值大于1的节点为根的子树,我们称为最小不平衡子树。
节点定义:
右旋操作:
左旋操作:
5 多路查找树
定义:多路查找树(mutil-way search tree),其每一个节点的孩子树可以多于两个,且每个节点处可存储多个元素。
6 散列表查找
定义:散列技术是在记录的存储位置和它的关键字之间建立一个确定的对应关系f,使得每个关键字key对应一个存储位置f(key)。
散列技术最适合的求解问题是查找与给定值相等的记录。
散列函数的构造方法:
直接地址法: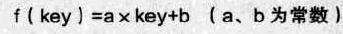
数字分析法:数字分析法通常适合处理关键字位数比较大的情况, 如果事先知道关键字的分布且关键字的诺干位分布较均匀,就可考虑数字分析法。
平方取中发:
折叠法:折叠法是将关键字从左到右分割成位数相等的几部分(注意最后一部分位数不够时可以短些),然后将这几部分叠加求和,并按散列列表表长,取后几位作为散列地址。
除留余数法:
随机数法:
总之,在现实中,应该视不同情况采用不同的散列函数,参考因素:

7 二叉排序树流程图
a 查找: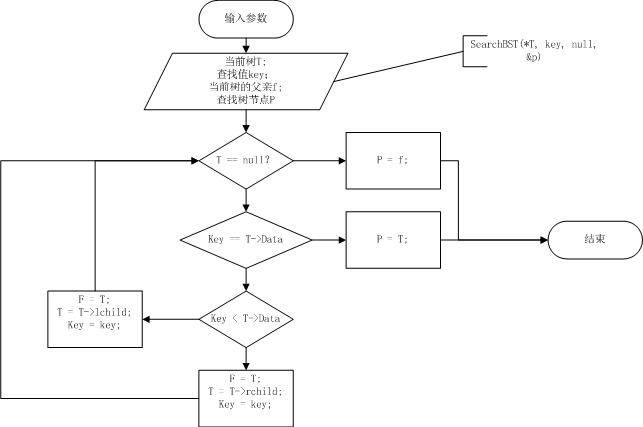
b 插入: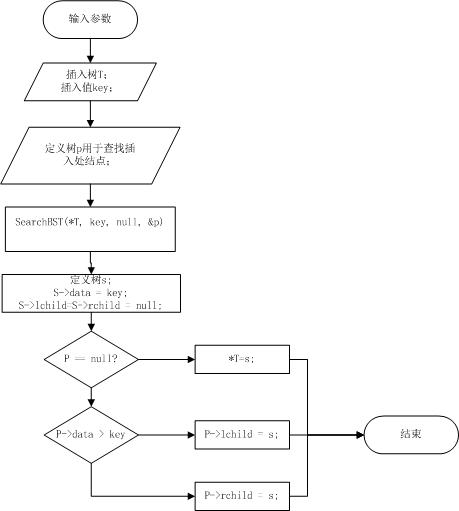
c 删除: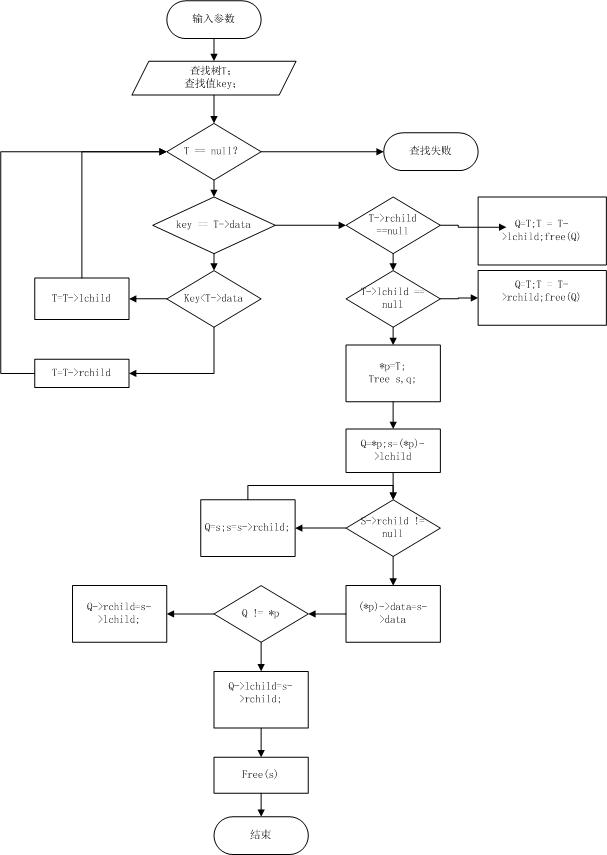
8 算法实现

1 public class BiTree 2 { 3 public int Data { get; set; } 4 public BiTree LChild { get; set; } 5 public BiTree RChild { get; set; } 6 7 public void CopyFrom(BiTree tree) 8 { 9 Data = tree.Data; 10 LChild = tree.LChild; 11 RChild = tree.RChild; 12 } 13 }

1 public static bool Search(BiTree searchTree, int data, BiTree parentTree, ref BiTree result) 2 { 3 if (searchTree == null) 4 { 5 result = parentTree; 6 return false; 7 } 8 else if (searchTree.Data == data) 9 { 10 result = searchTree; 11 return true; 12 } 13 else if (data < searchTree.Data) 14 { 15 return Search(searchTree.LChild, data, searchTree, ref result); 16 } 17 else 18 { 19 return Search(searchTree.RChild, data, searchTree, ref result); 20 } 21 }

1 public class InsertBST 2 { 3 public static bool Insert(BiTree tree, int data) 4 { 5 BiTree p = null, s = null; 6 if (SearchBST.Search(tree, data, null, ref p)) 7 { 8 //原树已经包含了该数据; 9 return false; 10 } 11 s = new BiTree {Data = data, LChild = null, RChild = null}; 12 if (data < p.Data) 13 { 14 p.LChild = s; 15 } 16 else 17 { 18 p.RChild = s; 19 } 20 return true; 21 } 22 }

1 public class DeleteBST 2 { 3 public static bool Delete(BiTree tree, BiTree parentTree, int data) 4 { 5 if (tree == null) 6 { 7 return false; 8 } 9 if (data == tree.Data) 10 { 11 return Delete(tree, parentTree); 12 } 13 else if (data < tree.Data) 14 { 15 return Delete(tree.LChild, tree, data); 16 } 17 else 18 { 19 return Delete(tree.RChild, tree, data); 20 } 21 } 22 23 private static bool Delete(BiTree tree, BiTree parentTree) 24 { 25 if (tree.LChild == null) 26 { 27 if (parentTree.LChild == tree) 28 { 29 parentTree.LChild = tree.RChild; 30 } 31 else 32 { 33 parentTree.RChild = tree.RChild; 34 } 35 } 36 else if (tree.RChild == null) 37 { 38 if (parentTree.LChild == tree) 39 { 40 parentTree.LChild = tree.LChild; 41 } 42 else 43 { 44 parentTree.RChild = tree.LChild; 45 } 46 } 47 else 48 { 49 BiTree q = tree; 50 BiTree s = tree.LChild; 51 while (s.RChild != null) 52 { 53 q = s; 54 s = s.RChild; 55 } 56 tree.Data = s.Data; 57 if (q != tree) 58 { 59 q.RChild = s.LChild; 60 } 61 else 62 { 63 q.LChild = s.LChild; 64 } 65 } 66 67 return true; 68 } 69 }
9 单元测试

1 private static void TestBinarySortTree() 2 { 3 var rootTree = new BiTree {Data = 34}; 4 InsertBST.Insert(rootTree, 45); 5 InsertBST.Insert(rootTree, 23); 6 InsertBST.Insert(rootTree, 56); 7 InsertBST.Insert(rootTree, 67); 8 InsertBST.Insert(rootTree, 21); 9 InsertBST.Insert(rootTree, 11); 10 InsertBST.Insert(rootTree, 25); 11 InsertBST.Insert(rootTree, 48); 12 InsertBST.Insert(rootTree, 22); 13 14 BiTree searchTree = null; 15 bool isSearch = SearchBST.Search(rootTree, 88, null, ref searchTree); 16 //当查找失败时验证 17 Assert.IsEqual(isSearch, false); 18 Assert.IsEqual(searchTree.Data, 67); 19 //当查找成功时验证 20 searchTree = null; 21 isSearch = SearchBST.Search(rootTree, 25, null, ref searchTree); 22 Assert.IsEqual(isSearch, true); 23 Assert.IsEqual(searchTree.Data, 25); 24 //删除功能验证 25 var isDeleted = DeleteBST.Delete(rootTree, null, 99); 26 Assert.IsEqual(isDeleted, false); 27 Assert.IsEqual(true, DeleteBST.Delete(rootTree, null, 23)); 28 Assert.IsEqual(false, SearchBST.Search(rootTree, 23, null, ref searchTree)); 29 }
最后附上源代码下载地址:
