Planning and Learning with Tabular Methods
在强化学习中有一种划分方式可以将算法大体分成两大类,一类是需要模型来刻画环境的算法(model-based),如动态编程和启发等;另一类算法则不需要环境模型(model-free),如MC与TD等。model-based 依赖计划(planning),而model-free则主要依靠学习。尽管如此,二者还是有许多相似之处,比如强化学习的大多数情况是要计算动作的价值函数的,二者也是如此,再比如几乎所有的方法都基于对未来态势的变化的预测,计算反向传播值。于是,有必要用一种统一的视角来讨论二两类方法。
Models and Planning
所谓环境模型指的是一切被用于agent预测环境对其动作的反应的信息。已知某一状态与动作,模型可以产生对下一状态动作与奖励的预测。如果模型是随机的(stochastic),即下一状态以不同概率的几种不同可能的分布,这样的模型称为分布模型(distribution models),如果下一状态以某概率产生一种可能,则称为抽样模型(sample models)。模型可用来模拟经验。
在强化学习中,所谓计划指的是任何计算过程,只要这个过程是以模型作为输入,输出策略(或更好的策略):
计划主要可划分为两种:一种称为状态空间计划,即在企图在状态空间找到最优策略;另一种为计划空间计划,即在计划的空间中找到最佳策略。现主要考虑第一种。所有的状态空间计划方法在优化策略时,都会将计算价值函数作为关键的中间步骤,且计算方式是应用在模拟经验上的反向更新操作:
无论学习还是计划都是要估计价值函数的,而学习与计划的主要区别在于学习使用产生于环境的真实的经验,而计划则是使用由环境模型产生的模拟数据。上述的通用框架也表明了学习与计划可以互相转化。下面的算法即是一个实例:
# Random-sample one-step tabular Q-planning
Loop forever:
1. Select a state, S in S and an action, A in A(S), at random
2. Send S, A to a sample model, and obtain a sample next reward, R, and a sample next state, S'
3. Apply one-step tabluar Q-learning to S,A,R,S':
Q(S,A) = Q(S,A) + alpha[R + gamma max_a Q(S',a) - Q(S,A)]
Dyna: Integrated Planning, Acting, and Learning
当在线执行计划时,会带来很多的问题,最突出的就是新的信息会改变环境模型,也就会改变所谓的计划。
Dyna-Q算法对此有些比好的处理。
在一个计划agent中,真实的经验至少有两个作用:用来提升环境模型,另一个是直接提升对价值函数或策略的估计。前者可称为模型学习(或间接学习),而后者则称为直接强化学习。经验与学习,计划之间的关系可用如下图刻画:
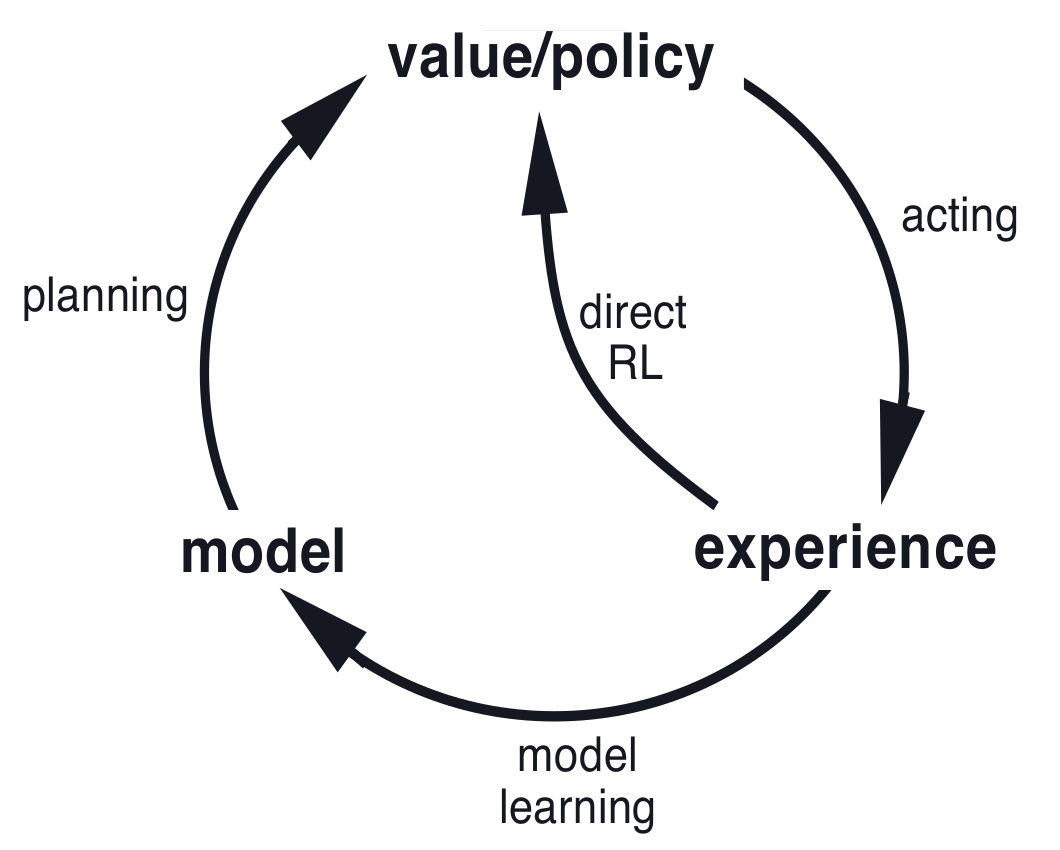
Dyna-Q包含上面的所有过程,计划算法使用的是random-sample one-step tabular Q-learning,直接学习算法则是one-step tabular Q-learning。
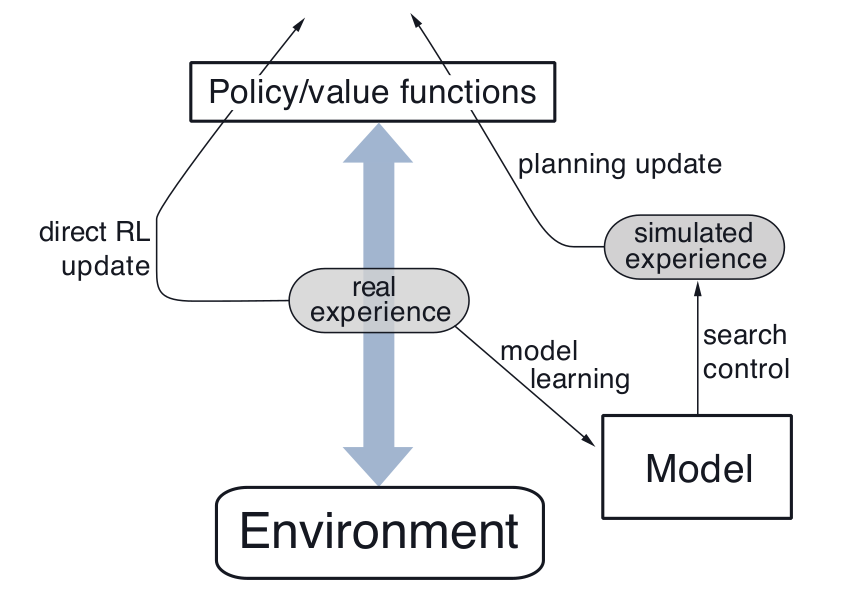
学习与计划深度整合,它们几乎共享所有机制,只不过经验来源不同。
# Tabular Dyna-Q
Initialize Q(s,a) and Model(s,a) (the contents of the (predicted next state and reward) for each state-pair (s,a)).
Loop forever:
a. S = current (nonterminal) state
b. A = e-greedy(S,Q)
c. Tale action A; oberve resultant reward, R, and state, S'
d. Q(S,A) = Q(S,A) + alpha[R + gamma max_a Q(S',a) - Q(S,A)]
e. Model(S,A) = R,S' (assuming determinstic environment)
f. Loop repeat n times:
S = random previously observeed state
A = random action previously taken in S
R,S' = Model(S,A)
Q(S,A) = Q(S,A) + alpha[R + gamma max_a Q(S',a) - Q(S,A)]
When the Model is Wrong
当(环境)模型不正确时,计划过程很可能得出一个次优策略。
Prioritized Sweeping
在Dyna agent中,模拟的经验是均匀随机抽取的,这是低效的。
# Prioritized sweeping for a determinstic environment
Initialize Q(s,a), Model(s,a), for all s,a and PQueue to empty
Loop forever:
a. S = current (nonterminal) state
b. A = policy(S,Q)
c. Take action A; observe resultant reward, R, and state,S'
d. Model(S,A) = R,S'
e. P = |R + gamma max_a Q(S',a) - Q(S,A)|
f. if P > theta, then insert S,A into PQueue with priority P
g. Loop repeat n times, while PQueue is not empty:
S,A = first(PQueue)
R,S' = Model(S,A)
Q(S,A) = Q(S,A) + alpha [R + gamma max_a Q(S',a) - Q(S,A)]
Loop for all S_bar, A_bar predicted to lead to S:
R_bar = predicted reward for S_bar, A_bar,S
p = |R_bar + gamma max_a Q(S,a) - Q(S_bar,A_bar)|
if P > theta then insert S_bar, A_bar into PQueue with priority P
Expected vs. Sample Updates
目前为止,我们提到了很多不同的价值函数更新的方法。特别地,对于一步更新来说,主要有三个维度考虑:
一是这些方法是否更新状态价值或者是动作价值;二是这些方法是否估计最优策略的价值或者任一给定策略的价值;三是这些方法的更新是否是期望(expected)更新(即考虑所有可能的事件)或者样本更新(sample,只考虑所抽样本)。这三个维度可以有八种组合方式,从而且生了七种不同的算法(有一种无意义):
e
下面来看下期望更新与抽样更新的区别: