风水。。。是一门艺术。。。我在想要不要看看《周易》《葬经》什么的,等老了还能出去给人算算命,看看阴宅阳宅什么的,混口饭吃。嘿嘿,扯远了。。。
题意:给一个凸多边形,然后在里面放两个半径为r的圆。问怎么放能使覆盖的面积最大(spj)。
思路:把多边形的每一条边向“内”移r的距离,交得一个新多边形。在多边形上找两个尽量圆的点,放上圆心。
关于怎么向内移动r的距离,见下图
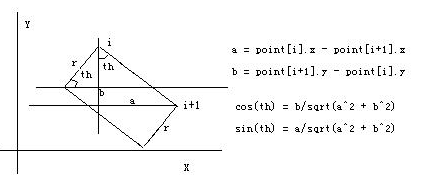
所以 point[i] 和 point[i+1] x轴上移动的距离就是r*cos(th), y轴上移动距离就是r*sin(th);
 View Code
View Code
//#pragma comment(linker,"/STACK:327680000,327680000") #include <iostream> #include <cstdio> #include <cmath> #include <vector> #include <cstring> #include <algorithm> #include <string> #include <set> #include <functional> #include <numeric> #include <sstream> #include <stack> #include <map> #include <queue> #define CL(arr, val) memset(arr, val, sizeof(arr)) #define REP(i, n) for((i) = 0; (i) < (n); ++(i)) #define FOR(i, l, h) for((i) = (l); (i) <= (h); ++(i)) #define FORD(i, h, l) for((i) = (h); (i) >= (l); --(i)) #define L(x) (x) << 1 #define R(x) (x) << 1 | 1 #define MID(l, r) (l + r) >> 1 #define Min(x, y) (x) < (y) ? (x) : (y) #define Max(x, y) (x) < (y) ? (y) : (x) #define E(x) (1 << (x)) #define iabs(x) (x) < 0 ? -(x) : (x) #define OUT(x) printf("%I64d\n", x) #define Read() freopen("data.in", "r", stdin) #define Write() freopen("data.out", "w", stdout); typedef long long LL; const double eps = 1e-8; const double PI = acos(-1.0); const int inf = ~0u>>2; using namespace std; const int maxn = 1010; struct Point { double x; double y; Point() {} Point(double a, double b): x(a), y(b) {} void input() { scanf("%lf%lf", &x, &y); } }; Point point[maxn], p[maxn], q[maxn]; //读入的多边形的顶点(顺时针)、p为存放最终切割得到的多边形顶点的数组、暂存核的顶点 int cCnt, n; //此时cCnt为最终切割得到的多边形的顶点数、暂存顶点个数 double r; inline int dbcmp(double x) { //精度问题 if(x > eps) return 1; else if(x < -eps) return -1; return 0; } inline void getline(Point x, Point y, double& a, double& b, double& c) { //点X,Y确定一条直线 a = y.y - x.y; b = x.x - y.x; c = y.x*x.y - x.x*y.y; } inline Point intersect(Point x, Point y, double a, double b, double c) { ////求x、y形成的直线与已知直线a、b、c、的交点 double u = fabs(a*x.x + b*x.y + c); double v = fabs(a*y.x + b*y.y + c); return Point((x.x*v + y.x*u)/(u + v), (x.y*v + y.y*u)/(u + v)); } inline void cut(double a, double b, double c) { //如上图所示,切割 int cur = 0, i; for(i = 1; i <= cCnt; ++i) { if(dbcmp(a*p[i].x + b*p[i].y + c) >= 0) q[++cur] = p[i]; // c由于精度问题,可能会偏小,所以有些点本应在右侧而没在 else { if(dbcmp(a*p[i-1].x + b*p[i-1].y + c) > 0) //如果p[i-1]在直线的右侧的话, //则将p[i],p[i-1]形成的直线与已知直线的交点作为核的一个顶点(这样的话,由于精度的问题,核的面积可能会有所减少) q[++cur] = intersect(p[i], p[i-1], a, b, c); if(dbcmp(a*p[i+1].x + b*p[i+1].y + c) > 0) q[++cur] = intersect(p[i], p[i+1], a, b, c); } } for(i = 1; i <= cur; ++i) p[i] = q[i]; p[cur+1] = q[1]; p[0] = p[cur]; cCnt = cur; } double ddis(Point a, Point b) { return sqrt((a.x - b.x)*(a.x - b.x) + (a.y - b.y)*(a.y - b.y)); } void solve() { //注意:默认点是顺时针,如果题目不是顺时针,规整化方向 int i, j; Point pa, pb, pt; double Cos, Sin; double a, b, c; for(i = 1; i <= n; ++i) { a = point[i].x - point[i+1].x; //point[]不是p[].... b = point[i+1].y - point[i].y; Cos = b/sqrt(a*a + b*b); Sin = a/sqrt(a*a + b*b); pt = Point(r*Cos, r*Sin); pa = Point(point[i].x + pt.x, point[i].y + pt.y); pb = Point(point[i+1].x + pt.x, point[i+1].y + pt.y); getline(pa, pb, a, b, c); cut(a, b, c); } double tmp, maxd = 0; int a1 = 0, a2 = 0; for(i = 1; i <= cCnt; ++i) { for(j = i + 1; j <= cCnt; ++j) { tmp = ddis(p[i], p[j]); //printf("%d %d %f\n", i, j, tmp); if(dbcmp(tmp - maxd) > 0) { maxd = tmp; a1 = i; a2 = j; } } } printf("%.4f %.4f %.4f %.4f\n", p[a1].x, p[a1].y, p[a2].x, p[a2].y); } void init() { int i; FOR(i, 1, n) point[i].input(); point[n+1] = point[1]; //初始化p[], cCnt FOR(i, 1, n) p[i] = point[i]; p[n+1] = p[1]; p[0] = p[n]; cCnt = n; } int main() { //freopen("data.in", "r", stdin); while(~scanf("%d%lf", &n, &r)) { init(); solve(); } return 0; }
