一、基本概念
# 图:是一种数学模型,表示信息之间的联系;
# 图的作用:通过可视化的图,可以比较容易的得出不同的结论;
# 图的模型的表示,主要是数据可视化要做的事;
# 算法中的图,主要由点和边组成的数学模型,表示真实样本的关系;
# 节点(Vertex)
# 边(Edge)
# 例1:快递网络,每个点是一个分拨中心,每各边表示分拨中心之间的距离;
# 例2:社交网络,每个点表示一个人,每个边表示人与人之间的关系;
# 例3:程序的状态执行,每个点表示程序的一个状态,每个边表示程序可以从一种状态执行到另一种状态;
# 分类:
# 方式(一):
# 1)无向图(UNdirected Graph):边不表示方向;
# 也可以将无向图看做是一种特殊的有向图,如下图:

# 2)有向图(Directed Graph):边有方向;
# 有向图中的点与点之间不对称,有时会出现一些更加复杂的问题,进而产生出一些专门的算法,一般有向图会涉及到比较难的算法;
# 很多时候是在研究有向图和无向图都通用的算法;
方式(二):
# 1)无权图(Unweighted Graph):
# 2)有权图(Weighted Graph):
# 权,可以理解为一个数值;
# 分类的方式是,有没有数值与连接节点与节点之间的边相对应;
# 例1(无权图):社交网络,点表示人,表可以表示认识 / 不认识这两种状态,并不是一个值;
# 例2(有权图):快递网络,点表分拨中心,边表示分拨中心之间的距离,是一直具体是数值;
# 图的连通性:
# 实际中,有的图不是完全连通的,分成不同的块,共同组成了各种关联;
# 简单图(Simple Graph):没有自环边和平行边的图;
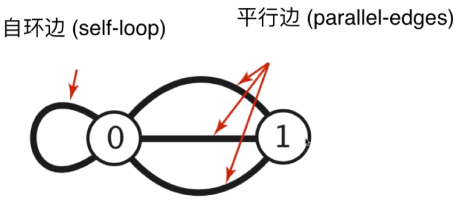
# 有时候,平行边和自环边会加大算法的难度;
二、图的表示
# 图的核心就是节点和连接节点的边;
# 一般表示方式的不同体现是对边的表示,应该用哪种数据结构;
# 方式(一):邻接矩阵(Adjacency Matrix)
# 使用一个 n X n 的二维矩阵表示一张图:n 就是图的节点数;
# 无向图的邻接矩阵关于对角线对称;
# 例:
# 一)无向图的表示法:

- X 矩阵中的第 Xij 个数据,表示第 i 个点与第 j 个点的关系;
- 0,表示两点不相连;1,表示两点相连;
# 二)有向图的表示法
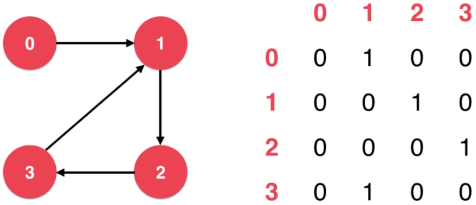
# 方式(二):邻接表(Adjacency Lists)
# 对应每一行数据,只表示与该行表示的点相连的点的信息;
# 1)无向图
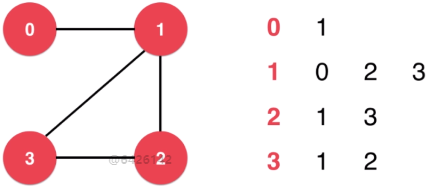
- 每一行表示一个点;
- 每一行的数据,表示与该点相连的点的名称;
# 每一行相当于一个链表,存放了对于该行而言,与该行表示的点邻的所有的点;
# 2)有向图
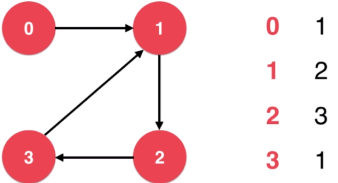
# 邻接矩阵与邻接表对比:
- 邻接表适合表示稀疏图(Sparse Graph),邻接矩阵适合表示稠密图(Dense Graph);
- 稀疏图使用邻接表存储,效率更高;
- 稀疏图:边相对较少的图;(边与点的数量比较小)
- 稠密图:边相对较多的图;(边与点的数量比较大)
- 如果有 k 个点,理论上,每一个点最多都能与其它 k-1 个点相连(完全图),则最多有 k*(k - 1) / 2 条边,边与点的最大比:(k - 1) / 2;
- 邻接表所占存储空间小;
# 完全图:每个点都与其它所有的点相连;
# 代码实现邻接表和邻接矩阵: