题目描述
组合数表示的是从n个物品中选出m个物品的方案数。举个例子,从(1,2,3) 三个物品中选择两个物品可以有(1,2),(1,3),(2,3)这三种选择方法。根据组合数的定 义,我们可以给出计算组合数的一般公式:
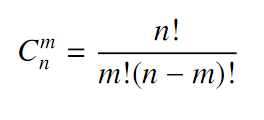
其中n! = 1 × 2 × · · · × n
小葱想知道如果给定n,m和k,对于所有的0 <= i <= n,0 <= j <= min(i,m)有多少对 (i,j)满足是k的倍数。
输入输出格式
输入格式:
第一行有两个整数t,k,其中t代表该测试点总共有多少组测试数据,k的意义见 【问题描述】。
接下来t行每行两个整数n,m,其中n,m的意义见【问题描述】。
输出格式:
t行,每行一个整数代表答案。
输入输出样例
输入样例#1:
1 2
3 3
输出样例#1:
1
输入样例#2:
2 5
4 5
6 7
输出样例#2:
0
7
说明
【样例1说明】
在所有可能的情况中,只有是2的倍数。
【子任务】

可以发现k是先给出的且不会变,想到先预处理出所有的答案
我们知道C(i,j)=C(i-1,j)+C(i-1,j-1),先用O(n^2)处理所有C[i][j]并取模
取b[i][j]表示c[i][j]是否能整除k,判断取模后是否为0即可
设f[i][[j]为对应的n=i,m=j的答案,分析f[i][j]的递推关系
其实打个表就容易找到规律,这里f[i][j]=C[i-1][j]+C[i][j-1]+C[i-1][j-1]+b[i][j]
代码如下,
#include <cstdio>
#include <cstring>
#define N 2020
int T, k, n, m;
int f[N][N];
bool b[N][N];
inline int read()
{
int x = 0, f = 1; char ch = getchar();
while (ch < '0' || ch > '9') {if (ch == '-')f = -1; ch = getchar();}
while (ch >= '0' && ch <= '9') {x = x * 10 + ch - '0'; ch = getchar();}
return x * f;
}
int main()
{
T = read(), k = read();
for (int i = 1; i <= N; ++i)
{
f[i][1] = i % k;
f[i][i] = 1;
}
for (int i = 3; i <= 2000; ++i)
for (int j = 2; j <= i - 1; ++j)
f[i][j] = (f[i - 1][j] + f[i - 1][j - 1]) % k;
for (int i = 1; i <= 2000; ++i)
for (int j = 1; j <= i; ++j)
if (!f[i][j]) b[i][j] = 1;
memset(f, 0, sizeof(f));
for (int i = 1; i <= 2000; ++i)
for (int j = 1; j <= 2000; ++j)
f[i][j] = f[i - 1][j] + f[i][j - 1] - f[i - 1][j - 1] + b[i][j];
while (T--)
{
n = read(), m = read();
printf("%d
", f[n][m]);
}
return 0;
}