判断一个点是否在多边形内部的典型方法:
(1)面积和判别法:判断目标点与多边形的每条边组成的三角形面积和是否等于该多边形,相等则在多边形内部。
(2)夹角和判别法:判断目标点与所有边的夹角和是否为360度,为360度则在多边形内部。
(3)光线投射法:从目标点出发引一条射线,看这条射线和多边形所有边的交点数目。如果有奇数个交点,则说明在内部,如果有偶数个交点,则说明在外部。
这里前两种方法我没有找到比较好的讲解,另外显而易见第三种方法最好想,所以这里我只放第三种方法的讲解。另外提醒大家使用第三种方法时一定要考虑好关于顶点的情况(例如: 过点算不算相交;当射线与边重合怎么算;顶点是否可能被记两次等等)
以下内容转载自:点击打开链接
“判断一个点是否在一个多边形里”,一开始以为是个挺难的问题,但Google了一下之后发现其实蛮简单,所用到的算法叫做“Ray-casting Algorithm”,中文应该叫“光线投射算法”,这是维基百科的描述:维基百科
简单地说可以这么判断:从这个点引出一根“射线”,与多边形的任意若干条边相交,累计相交的边的数目,如果是奇数,那么点就在多边形内,否则点就在多边形外。
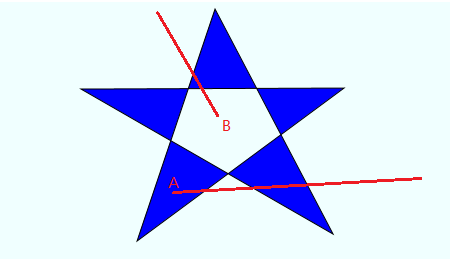
如图,A点引一条射线,与多边形3条边相交,奇数,所以A点在多边形内,而从B点引一条射线,与多边形的2条边相交,偶数,所以B点在多边形外。
我打算把这个算法用于判断地图上所在的位置是否在一个范围之内,我先用鼠标在地图上绘制出一个多边形区域,然后再用这个方法判断一个坐标是否在这个多边形范围内,我仍然拿五角星做试验品,在高德地图上描出一个五角星:
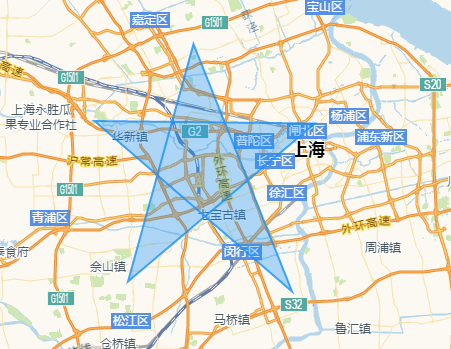
嗯?怎么五角星居然中间没被镂空?这是怎么回事?经过研究,我发现高德地图的鼠标工具的多边形填充用的是另外一套规则,叫做“None Zero Mode”,判断一个点是否在多边形内的规则就变成了:从这个点引出一根“射线”,与多边形的任意若干条边相交,计数初始化为0,若相交处被多边形的边从左到右切过,计数+1,若相交处被多边形的边从右到左切过,计数-1,最后检查计数,如果是0,点在多边形外,如果非0,点在多边形内。回到五角星的例子,这次要注意多边形线条描绘的方向:
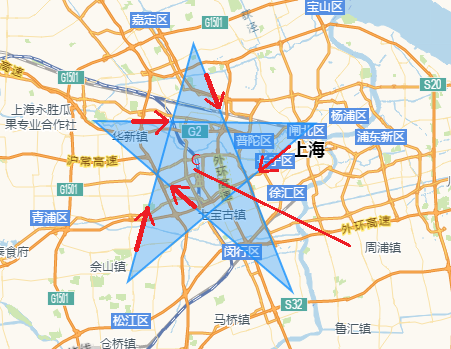
从C点引出一条射线,与这条射线相交的两条多边形的边均是从左向右切过,总计数是2,因此C点在多边形内。用个更形象点的方式描述就是:从C点出发,一直朝一个方向走,遇到两条单行道,都是从自己的左边切至右边的方向,计数+1,计数+1,总计数所以是2。
算法实现起来居然很简单,几行代码即可,真的是几行代码,我用的是C#,大家可以轻轻松松改成别的。
public static class RayCastingAlgorithm {
public static bool IsWithin(Point pt, IList<Point> polygon, bool noneZeroMode) {
int ptNum = polygon.Count();
if (ptNum < 3) {
return false;
}
int j = ptNum - 1;
bool oddNodes = false;
int zeroState = 0;
for (int k = 0; k < ptNum; k++) {
Point ptK = polygon[k];
Point ptJ = polygon[j];
if (((ptK.Y > pt.Y) != (ptJ.Y > pt.Y)) && (pt.X < (ptJ.X - ptK.X) * (pt.Y - ptK.Y) / (ptJ.Y - ptK.Y) + ptK.X)) {
oddNodes = !oddNodes;
if (ptK.Y > ptJ.Y) {
zeroState++;
}
else {
zeroState--;
}
}
j = k;
}
return noneZeroMode?zeroState!=0:oddNodes;
}
}