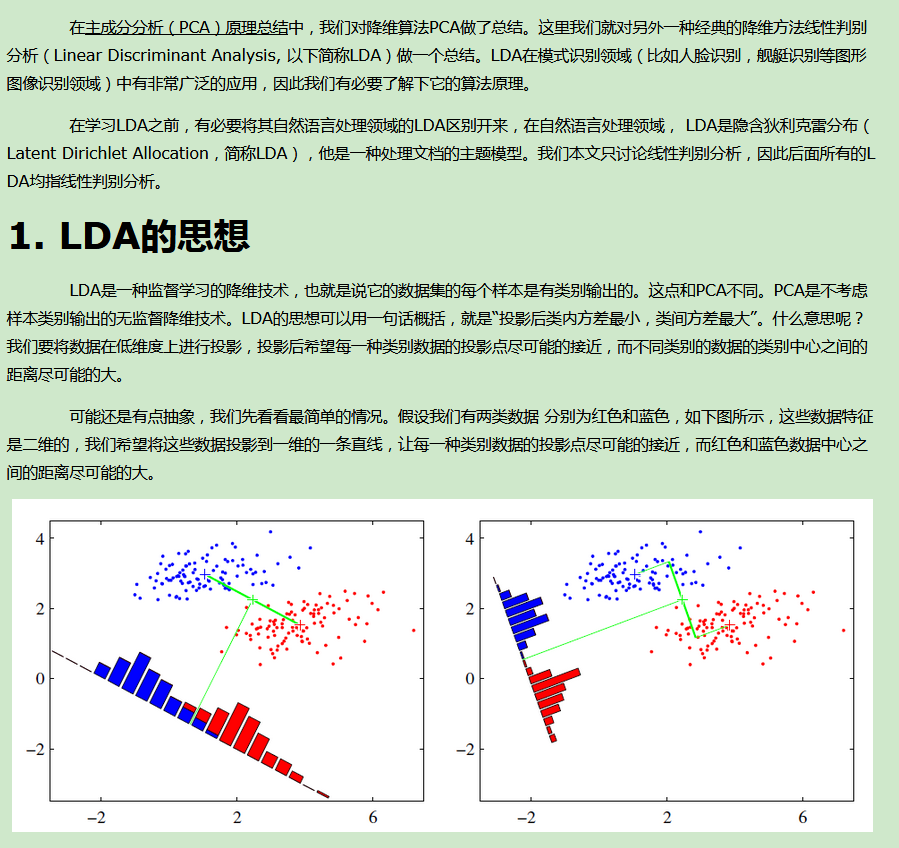
在线性判别分析LDA原理总结中，我们对LDA降维的原理做了总结，这里我们就对scikit-learn中LDA的降维使用做一个总结。
1. 对scikit-learn中LDA类概述
在scikit-learn中， LDA类是sklearn.discriminant_analysis.LinearDiscriminantAnalysis。那既可以用于分类又可以用于降维。当然，应用场景最多的还是降维。和PCA类似，LDA降维基本也不用调参，只需要指定降维到的维数即可。
2. LinearDiscriminantAnalysis类概述
我们这里对LinearDiscriminantAnalysis类的参数做一个基本的总结。
1）solver : 即求LDA超平面特征矩阵使用的方法。可以选择的方法有奇异值分解"svd"，最小二乘"lsqr"和特征分解"eigen"。一般来说特征数非常多的时候推荐使用svd，而特征数不多的时候推荐使用eigen。主要注意的是，如果使用svd，则不能指定正则化参数shrinkage进行正则化。默认值是svd
2）shrinkage：正则化参数，可以增强LDA分类的泛化能力。如果仅仅只是为了降维，则一般可以忽略这个参数。默认是None，即不进行正则化。可以选择"auto",让算法自己决定是否正则化。当然我们也可以选择不同的[0,1]之间的值进行交叉验证调参。注意shrinkage只在solver为最小二乘"lsqr"和特征分解"eigen"时有效。
3）priors ：类别权重，可以在做分类模型时指定不同类别的权重，进而影响分类模型建立。降维时一般不需要关注这个参数。
4）n_components：即我们进行LDA降维时降到的维数。在降维时需要输入这个参数。注意只能为[1,类别数-1)范围之间的整数。如果我们不是用于降维，则这个值可以用默认的None。
从上面的描述可以看出，如果我们只是为了降维，则只需要输入n_components,注意这个值必须小于“类别数-1”。PCA没有这个限制。
3. LinearDiscriminantAnalysis降维实例
在LDA的原理篇我们讲到，PCA和LDA都可以用于降维。两者没有绝对的优劣之分，使用两者的原则实际取决于数据的分布。由于LDA可以利用类别信息，因此某些时候比完全无监督的PCA会更好。下面我们举一个LDA降维可能更优的例子。
我们首先生成三类三维特征的数据，代码如下：
1 import numpy as np 2 import matplotlib.pyplot as plt 3 from mpl_toolkits.mplot3d import Axes3D 4 %matplotlib inline 5 from sklearn.datasets.samples_generator import make_classification 6 X, y = make_classification(n_samples=1000, n_features=3, n_redundant=0, n_classes=3, n_informative=2, 7 n_clusters_per_class=1,class_sep =0.5, random_state =10) 8 fig = plt.figure() 9 ax = Axes3D(fig, rect=[0, 0, 1, 1], elev=30, azim=20) 10 plt.scatter(X[:, 0], X[:, 1], X[:, 2],marker='o',c=y)
我们看看最初的三维数据的分布情况：
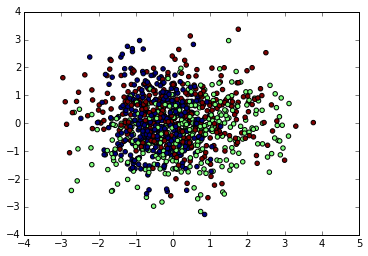
首先我们看看使用PCA降维到二维的情况，注意PCA无法使用类别信息来降维，代码如下：
from sklearn.decomposition import PCA pca = PCA(n_components=2) pca.fit(X) print pca.explained_variance_ratio_ print pca.explained_variance_ X_new = pca.transform(X) plt.scatter(X_new[:, 0], X_new[:, 1],marker='o',c=y) plt.show()
在输出中，PCA找到的两个主成分方差比和方差如下：
[ 0.43377069 0.3716351 ] [ 1.20962365 1.03635081]
输出的降维效果图如下:
由于PCA没有利用类别信息，我们可以看到降维后，样本特征和类别的信息关联几乎完全丢失。
现在我们再看看使用LDA的效果，代码如下：
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis lda = LinearDiscriminantAnalysis(n_components=2) lda.fit(X,y) X_new = lda.transform(X) plt.scatter(X_new[:, 0], X_new[:, 1],marker='o',c=y) plt.show()
输出的效果图如下：
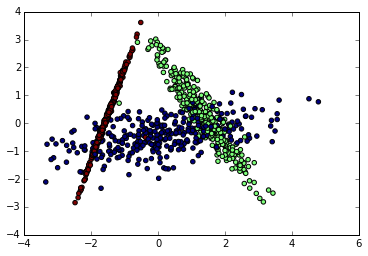
可以看出降维后样本特征和类别信息之间的关系得以保留。
一般来说，
如果我们的数据是有类别标签的，那么优先选择LDA去尝试降维；当然也可以使用PCA做很小幅度的降维去消去噪声，然后再使用LDA降维。
如果没有类别标签，那么肯定PCA是最先考虑的一个选择了。
线性判别分析LDA原理总结
https://www.cnblogs.com/pinard/p/6244265.html
