做一件事,要先想好思路,然后再制定一个方案,最后再解决它,写程序也是如此。
全排列有两种实现方式,一种是递归分治,另一种是字典序法。前者代码简洁,思维简单,但是耗费内存资源过大,并且不懂递归原理的人看代码有些吃力,介于此,请先查看鄙人写的《递归详解》一博文,后者代码量大,但思路清晰,节省内存资源。本章教大家用递归分治法实现全排列。
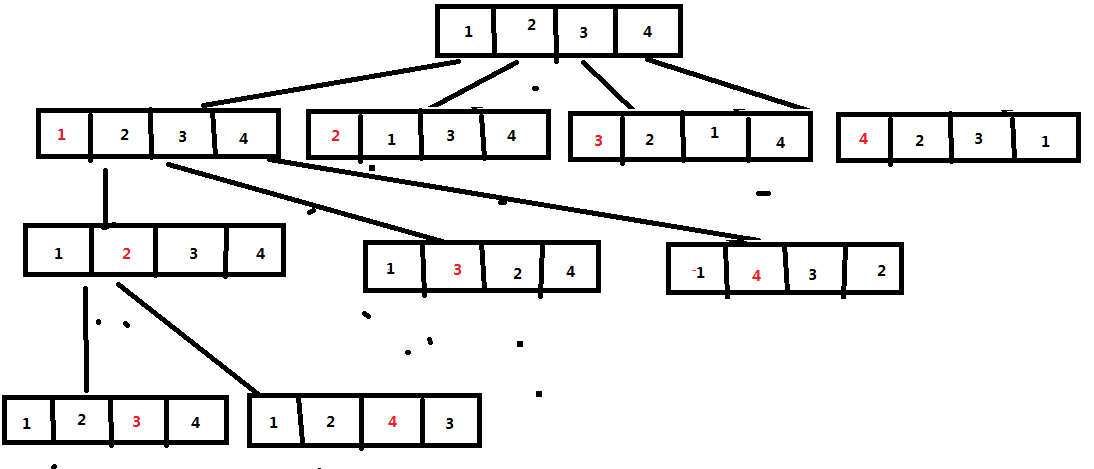
具体思路:先让一组数据(长度为n)的第一个与后几位依次进行交换,交换结果保留,然后分成n组,然后再固定第一位,让改组数据的第二位与后几位依次进行交换,然后分成n*(n-1)组,交换结果保留,依次类推,直到固定最后一位,最后一批的 n!(n的阶乘) 组数据即为所有数据的全排列!
图解如下:
因为数据庞大,顾只显示部分数据.
代码如下:
#include<iostream>
using namespace std;
void swap(int array[],int m,int n); //交换函数
void resault(int array[],int length,int sign); //最终解函数,可以直接写在主函数,但会导致头重脚轻,影响代码美观度。
void veiw(int array[],int length); //打印数据的函数
int main(int argc,char** argv){
int data[4] = {1,2,3,4};
resault(data,4,0);
return 0;
}
void view(int array[],int length){
for(int i = 0;i < length;i++){
cout << array[i] << " ";
}
cout << endl;
}
void resault(int array[],int length,int sign){
if(sign == length){
view(array,length);
}
for(int i = sign;i < length;i++){ //将标志位与后面n位依次进行交换,直到最后一位
swap(array,sign,i);
resault(array,length,sign + 1);
swap(array,sign,i); //还原上一步的状态,因为同等级递归原函数必须相同,如果不还原,会导致第n个同等级的递归原函数是基于同等级的前一个(n - 1)个递归原函数进行变换的,而不是基于上一个等级。
}
}
void swap(int array[],int m,int n){
int temp;
temp = array[m];
array[m] = array[n];
array[n] = temp;
}