JAVA数据结构--AVL树的实现

AVL树的定义

在计算机科学中，AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为1，所以它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下的时间复杂度都是 $O(log{n})$

节点的平衡因子是它的左子树的高度减去它的右子树的高度（有时相反）。带有平衡因子1、0或 -1的节点被认为是平衡的。带有平衡因子 -2或2的节点被认为是不平衡的，并需要重新平衡这个树。平衡因子可以直接存储在每个节点中，或从可能存储在节点中的子树高度计算出来。

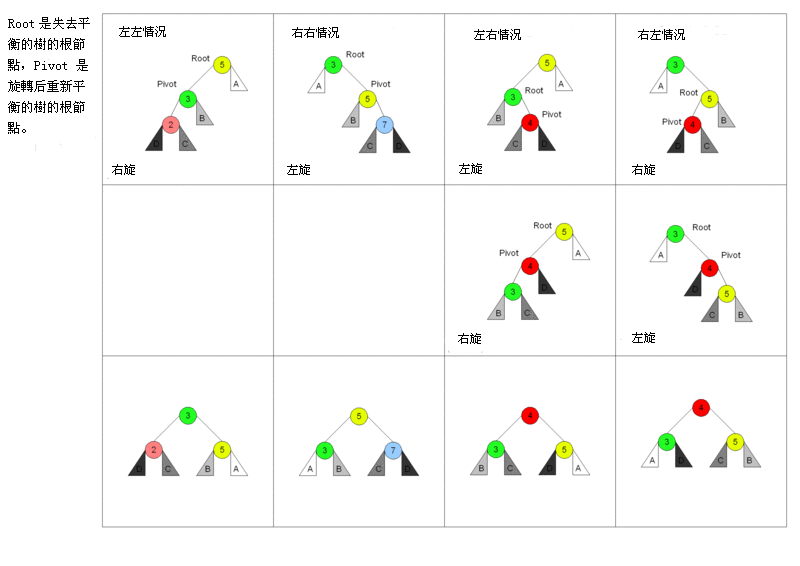
　　上图是摘自维基百科的AVL树实现的图例，比较清晰的解释了AVL调整平衡的过程。ABCD代表当前节点有子树。

　　我以我个人理解以左右情况为例

　　该例是左右情况，需要将其调整为左左或者右右才能继续调整。因为节点5是在右，所以3节点（虚线方框内）调整为左为最佳。左旋转即可使树变为左左形状。

AVL树节点定义

 1 private static class AvlNode<T>{
 2         public AvlNode(T theElement) {
 3             this(theElement, null, null);
 4         }
 5         public AvlNode(T theElement,AvlNode<T> lt,AvlNode<T> rt) {
 6             element=theElement;
 7             left=lt;
 8             right=rt;
 9             height=0;
10         }
11         T element;
12         AvlNode<T> left;
13         AvlNode<T> right;
14         int height;
15     }

与二叉查找树的定义类似，不过加入了节点的深度height定义。

AVL节点计算方法

1 private int height(AvlNode<T> t) {
2         return t==null?-1:t.height;
3 }

当banlance()或者旋转时height都会改变

节点旋转

 1 /*
 2      * 实现单旋转
 3      * */
 4     private AvlNode<T> rotateWithLeftChild(AvlNode<T> k2){//单左旋转
 5         AvlNode<T> k1=k2.left;
 6         k2.left=k1.right;
 7         k1.right=k2;
 8         k2.height=Math.max(height(k2.left), height(k2.right))+1;
 9         k1.height=Math.max(height(k1.left), k2.height)+1;
10         return k1;
11     }
12     private AvlNode<T> rotateWithRightChild(AvlNode<T> k1){//单右旋转
13         AvlNode<T> k2=k1.right;
14         k1.right=k2.left;
15         k2.left=k1;
16         k2.height=Math.max(height(k1.left), height(k1.right))+1;
17         k1.height=Math.max(height(k2.right), k1.height)+1;
18         return k2;
19     }
20     /*
21      * 实现双旋转
22      * 
23      * */
24     private AvlNode<T> doubleWithLeftChild(AvlNode<T> k3){//先右旋转再左旋转
25         k3.left=rotateWithRightChild(k3.left);
26         return rotateWithLeftChild(k3);
27     }
28      private AvlNode<T> doubleWithRightChild( AvlNode<T> k1 ){//先左旋转再右旋转
29          k1.right = rotateWithLeftChild( k1.right );
30          return rotateWithRightChild( k1 );
31     }

balance()方法的实现

 1 private AvlNode<T> balance(AvlNode<T> t){
 2         if(t==null)
 3             return t;
 4         if(height(t.left)-height(t.right)>ALLOWED_IMBALANCE) {//左子树高度过高
 5             if(height(t.left.left)>=height(t.left.right))//判断进行单旋转还是双旋转
 6                 t=rotateWithLeftChild(t);
 7             else
 8                 t=doubleWithLeftChild(t);
 9         }
10         else if (height(t.right)-height(t.left)>ALLOWED_IMBALANCE) {//右子树高度过高
11             if(height(t.right.right)>=height(t.right.left))
12                 
13                 
14                 
15                 t=rotateWithRightChild(t);
16             else
17                 t=doubleWithRightChild(t);
18         }
19         t.height=Math.max(height(t.left), height(t.right))+1;
20         return t;
21     }

删除节点方法

 1 private AvlNode<T> remove(T x,AvlNode<T> t){
 2          if(t==null)
 3              return t;
 4          int compareResult=x.compareTo(t.element);
 5          if(compareResult<0)
 6              t.left=remove(x, t.left);//递归查找删除
 7          else if (compareResult>0) {
 8             t.right=remove(x, t.right);
 9         }
10          else if (t.left!=null&&t.right!=null) {//要删除的节点两个孩子节点的情况
11              t.element=findMin(t.right).element;//从右子树中找出最小的节点替换当前要删除的节点
12              t.right=remove(t.element, t.right);//删除右子树中需要拿出替换的节点
13         }
14          else {
15             t=(t.left!=null)?t.left:t.right;//单个子节点的情况
16         }
17          return balance(t);
18      }

完整代码如下（不含遍历），github地址

  1 package Tree;
  2 public class AvlTree <T extends Comparable<? super T>>{
  3     private static class AvlNode<T>{
  4         public AvlNode(T theElement) {
  5             this(theElement, null, null);
  6         }
  7         public AvlNode(T theElement,AvlNode<T> lt,AvlNode<T> rt) {
  8             element=theElement;
  9             left=lt;
 10             right=rt;
 11             height=0;
 12         }
 13         T element;
 14         AvlNode<T> left;
 15         AvlNode<T> right;
 16         int height;
 17     }
 18     private AvlNode<T> root;//定义根节点
 19     public AvlTree() {
 20         root=null;
 21     }
 22     public int height() {
 23         return height(root);
 24     }
 25     public void insert(T x) {
 26         insert(x, root);
 27     }
 28     public void remove(T x) {
 29         root=remove(x,root);
 30     }
 31     private int height(AvlNode<T> t) {
 32         return t==null?-1:t.height;
 33     }
 34     private AvlNode<T> insert(T x,AvlNode<T> t){
 35         if(t==null)
 36             return new AvlNode<T>(x, null, null);
 37         int compareResult=x.compareTo(t.element);
 38         if(compareResult<0) {
 39             t.left=insert(x, t.left);
 40         }
 41         else if(compareResult>0){
 42             t.right=insert(x, t.right);
 43         }
 44         else {
 45             
 46         }
 47         return balance(t);
 48         
 49     }
 50     private AvlNode<T> balance(AvlNode<T> t){
 51         if(t==null)
 52             return t;
 53         if(height(t.left)-height(t.right)>ALLOWED_IMBALANCE) {//左子树高度过高
 54             if(height(t.left.left)>=height(t.left.right))//判断进行单旋转还是双旋转
 55                 t=rotateWithLeftChild(t);
 56             else
 57                 t=doubleWithLeftChild(t);
 58         }
 59         else if (height(t.right)-height(t.left)>ALLOWED_IMBALANCE) {//右子树高度过高
 60             if(height(t.right.right)>=height(t.right.left))
 61                 
 62                 
 63                 
 64                 t=rotateWithRightChild(t);
 65             else
 66                 t=doubleWithRightChild(t);
 67         }
 68         t.height=Math.max(height(t.left), height(t.right))+1;
 69         return t;
 70     }
 71     /*
 72      * 实现单旋转
 73      * */
 74     private AvlNode<T> rotateWithLeftChild(AvlNode<T> k2){//单左旋转
 75         AvlNode<T> k1=k2.left;
 76         k2.left=k1.right;
 77         k1.right=k2;
 78         k2.height=Math.max(height(k2.left), height(k2.right))+1;
 79         k1.height=Math.max(height(k1.left), k2.height)+1;
 80         return k1;
 81     }
 82     private AvlNode<T> rotateWithRightChild(AvlNode<T> k1){//单右旋转
 83         AvlNode<T> k2=k1.right;
 84         k1.right=k2.left;
 85         k2.left=k1;
 86         k2.height=Math.max(height(k1.left), height(k1.right))+1;
 87         k1.height=Math.max(height(k2.right), k1.height)+1;
 88         return k2;
 89     }
 90     /*
 91      * 实现双旋转
 92      * 
 93      * */
 94     private AvlNode<T> doubleWithLeftChild(AvlNode<T> k3){//先右旋转再左旋转
 95         k3.left=rotateWithRightChild(k3.left);
 96         return rotateWithLeftChild(k3);
 97     }
 98      private AvlNode<T> doubleWithRightChild( AvlNode<T> k1 ){//先左旋转再右旋转
 99          k1.right = rotateWithLeftChild( k1.right );
100          return rotateWithRightChild( k1 );
101     }
102      private AvlNode<T> remove(T x,AvlNode<T> t){
103          if(t==null)
104              return t;
105          int compareResult=x.compareTo(t.element);
106          if(compareResult<0)
107              t.left=remove(x, t.left);//递归查找删除
108          else if (compareResult>0) {
109             t.right=remove(x, t.right);
110         }
111          else if (t.left!=null&&t.right!=null) {//要删除的节点两个孩子节点的情况
112              t.element=findMin(t.right).element;//从右子树中找出最小的节点替换当前要删除的节点
113              t.right=remove(t.element, t.right);//删除右子树中需要拿出替换的节点
114         }
115          else {
116             t=(t.left!=null)?t.left:t.right;//单个子节点的情况
117         }
118          return balance(t);
119      }
120      private AvlNode<T> findMin(AvlNode<T> t){
121             //非递归写法
122             if(t!=null)
123                 while(t.left!=null)
124                     t=t.left;
125             return t;
126             //递归写法
127             /*if(t==null)
128                 return null;
129             else if (t.left==null) {
130                 return t;
131             }
132             return findMin(t.left);*/
133         }
134     private static final int ALLOWED_IMBALANCE=1;
135     
136 }

View Code

相关阅读:
MySQL分区性能初探
 FastDFS开源的轻量级分布式文件系统
 MySQL数据类型之数值类型，对理解类型定义中的“位”有莫大的帮助
 空密码引发共享打印机拒绝访问
 利用Myxls导出并下载Excel
StyleCop SA0102
Spring AOP介绍
 大学英语一下重修听力考试范围.doc 听力原文及MP3
Eclipse中文版
 飞鱼秀下载
原文地址：https://www.cnblogs.com/vi3nty/p/7904948.html