• AVL平衡二叉查找树

    二叉排序树：

    定义

            二叉排序树，又叫二叉查找树，它或者是一棵空树；或者是具有以下性质的二叉树： 
            1. 若它的左子树不空，则左子树上所有节点的值均小于它的根节点的值； 
            2. 若它的右子树不空，则右子树上所有节点的值均大于它的根节点的值； 
            3. 它的左右子树也分别为二叉排序树。
       比如下图就是一棵普通的二叉排序树：

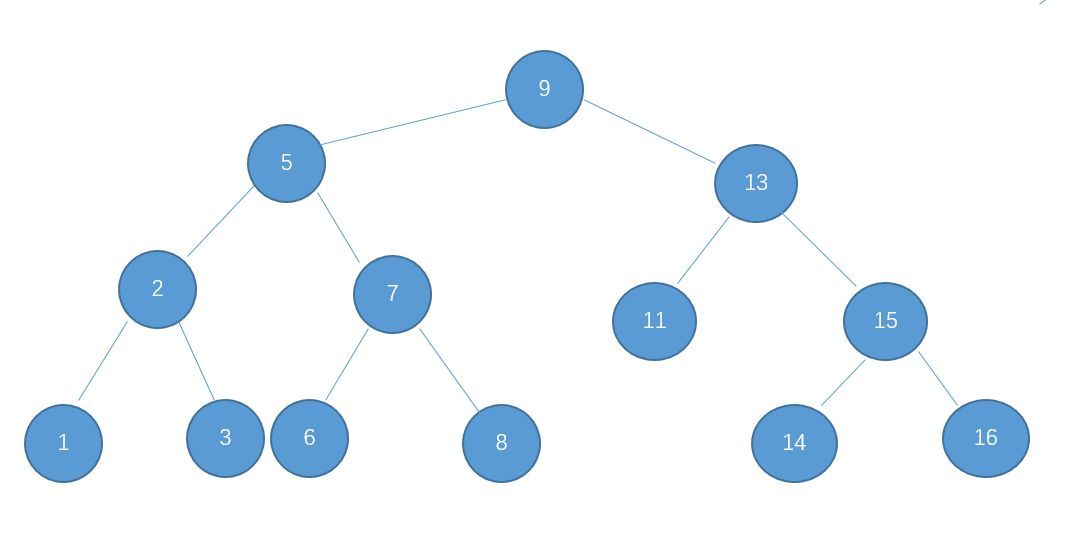
    在这里插入图片描述

       如果按照中序遍历的顺序，一棵二叉排序树的输出结果就刚好是按照从小到大的顺序输出的，可以运用于二分算法。

    先对其数据结构进行定义：

    typedef struct Binary_Tree_node
{
	int data;	//数据域
	struct Binary_Tree_node* lchild, * rchild;		//左右孩子结点
	
}Binode, * BiTree;

    然后是插入操作：

    //假设没有相等的data,这里我们不考虑相等的数据
//插入结点
void Insert_Binary_Tree(BiTree& bst ,int t)			//bst是根节点
{

	if (bst == NULL)	//空树或者递归到了叶结点
	{
		BiTree newp = new Binode;
		newp->data = t;
		newp->lchild = NULL;
		newp->rchild = NULL;
		bst = newp;	
	}
	else
	{
		if (t > bst->data)		//比本结点大，则插入其右孩子结点，小就插入左孩子结点
			Insert_Binary_Tree(bst->rchild, t);
		else
			Insert_Binary_Tree(bst->lchild, t);
	}	
}

    创建一棵树：

    //创建一棵二叉排序树
BiTree Create_Binary_Tree()
{
	BiTree bst = NULL;
	int t;
	cin >> t;
	while (t != ENDKEY)			//只要输入不等于-1，就一直往树里插入元素
	{
		Insert_Binary_Tree(bst, t);
		cin >> t;
	}
	return bst;
}

    删除操作：删除操作比较复杂，本篇博客主要是记录AVL，所以此处不做赘述

    BiTree Delete_Binary_Tree(BiTree bst, int t)
{
	Binode* newp, * f, * s, * q;	
	newp = bst;
	f = NULL;
	while (newp)					
	{
		if (newp->data == t)
			break;
		f = newp;				
		if (t > newp->data)
			newp = newp->rchild;
		else
			newp = newp->lchild;
	}
	if (newp == NULL)				
		return bst;
	if (newp->lchild == NULL)
	{
		if (f == NULL)					
			 bst = bst->rchild;
		else if (f->lchild == newp)
			f->lchild = newp->rchild;
		else							
			f->rchild = newp->rchild;

		delete[]newp;			
	}
	else if (newp->rchild == NULL)		
	{
		if (f == NULL)
			bst = bst->lchild;
		else if (f->lchild == newp)
			f->lchild = newp->lchild;
		else
			f->rchild = newp->lchild;

		delete[]newp;
	}
	else				
	{
		q = newp;
		s = newp->lchild;
		while (s->rchild)
		{
			q = s;				
			s = s->rchild;		
		}
		if (q == newp)
			q->lchild = s->lchild;	
		else	
			q->rchild = s->lchild;
		newp->data = s->data;
		delete[]s;
	}
	return bst;
}

    搜索二叉树：

    //搜索二叉树,根据输入的数据搜索二叉树，返回这个数据的结点
BiTree Search_Binary_Tree(BiTree bst, int t)
{
	if (bst == NULL)
		return NULL;
	if (bst->data == t)
		return bst;
	else if (t > bst->data)
		return Search_Binary_Tree(bst->rchild, t);
	else
		return Search_Binary_Tree(bst->lchild, t);
}

    平衡二叉排序树：

    可是当一棵二叉排序树的某个节点的一枝相比于另一枝太长，搜索的时间复杂度就会变成O(n)，而为了提高效率，提出了AVL树，即平衡二叉排序树。 例如下图就是一棵不平衡的二叉树：

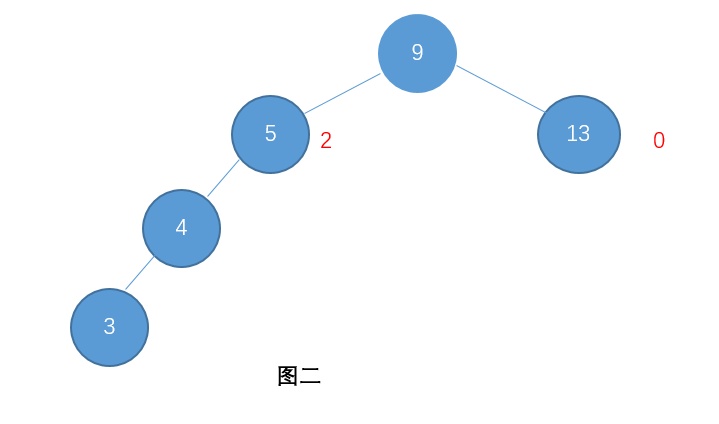
    在这里插入图片描述
    像这样如果要搜索0元素就会变得和线性表的时间复杂度一样。 AVL树是一种比查找二叉树还特别的树，这种树就可以帮助我们解决二叉查找树刚才的那种所有节点都倾向一边的缺点的。具有如下特性：
    1、具有二叉查找树的全部特性。
    2、每个节点的左子树和右子树的高度差至多等于1。
    例如：图一就是一颗AVL树了，而图二则不是(节点右边标的是这个节点的高度)。
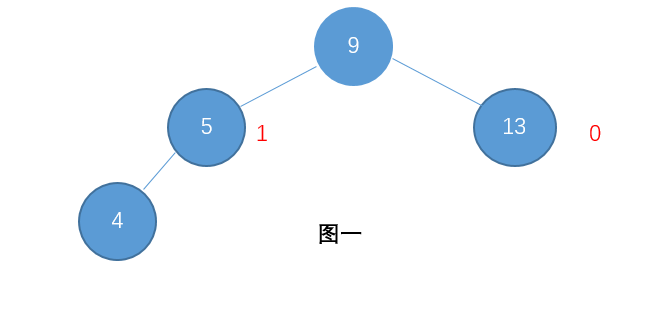
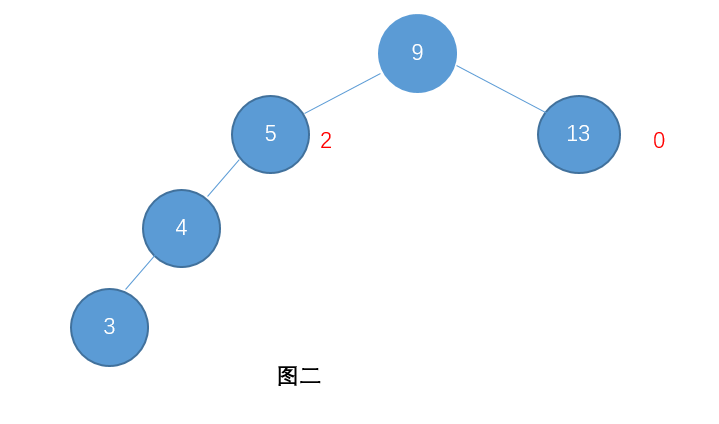
    在这里插入图片描述
    在这里插入图片描述
    按照这种规则进行建立二叉树，可以保证这棵二叉树始终是左右相对平衡的，可以保证搜索的时间复杂度达到O(log n)，提高了效率。

    针对树的失衡有四种情况，我们总结如下：
    1、左左型：做右旋
    2、右右型：做左旋
    3、左右型：先左旋，再右旋
    4、右左型：先右旋，再左旋

    下面一个一个写，对于实现每个旋转的函数可以作为私有的对内接口（C++），不对外开放使用

    1、左左型：做右旋：

    像下面这种：
    file
    我们做如下右旋操作：
    file
    即顺时针旋转结点，使双亲结点被自己的左孩子替代，然后自己变成左孩子结点的右孩子结点

    代码实现：

    		  //左左型单旋转
		  void Lleft(BiTree &bst)			//bst为不平衡的结点
		  {
	       BiTree lch = bst->lchild;		//保存不平衡结点的左孩子结点
	       bst->lchild = lch->rchild;
	       lch->rchild = bst;
	       bst = lch;
          }

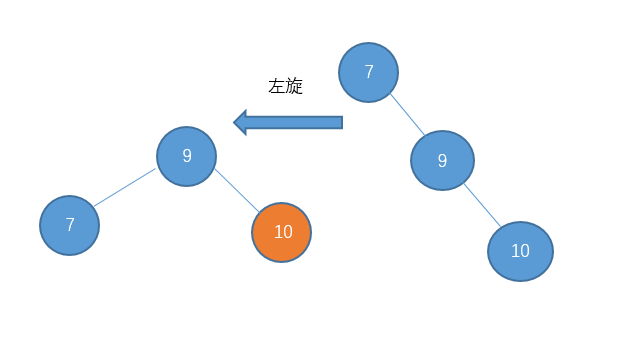
    2、右右型：做左旋：

    像下面这种：
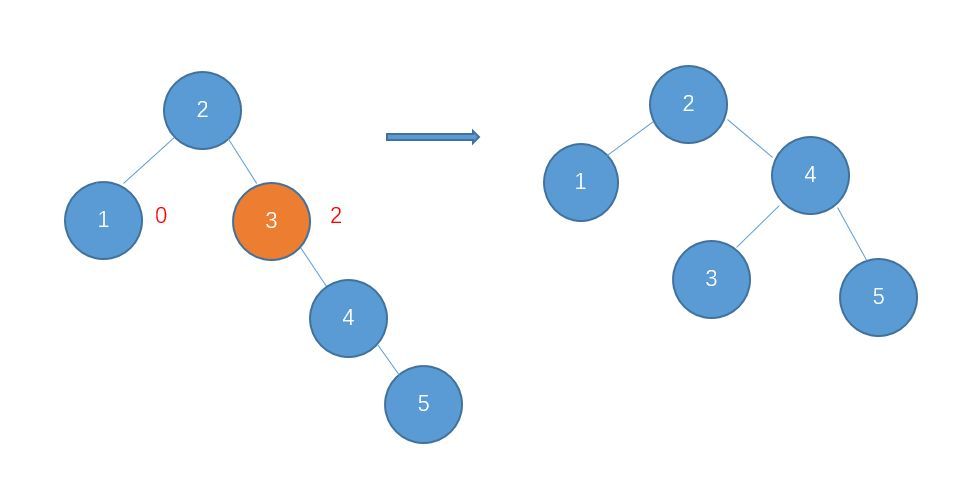
    在这里插入图片描述
    逆时针旋转结点，使自己被自己的右孩子替代，然后自己变成右孩子的左孩子结点

    代码实现：

    //右右型单旋转
void Rright(BiTree &bst)			//bst为不平衡的结点
{
	BiTree rch = bst->rchild;		//保存不平衡结点的右孩子结点
	bst->rchild = rch->lchild;
	rch->lchild = bst;
	bst = rch;
}

    3、左右型：先左旋，再右旋：

    像下面这种：
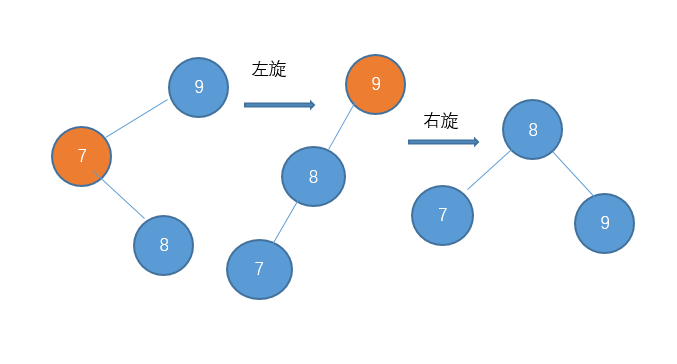
    在这里插入图片描述
    先对其左旋将其变成左左型，再右旋让其平衡

    代码实现：

    //左右型双旋转
void Lright(BiTree &bst)
{
	//先做左旋，将其变成左左型
	BiTree lch = bst->lchild;
	BiTree lrch = bst->lchild->rchild;
	bst->lchild = lrch;
	bst->lchild->lchild = lch;
	bst->lchild->lchild->rchild = NULL;		//可能存在bug	todo,目前来看没有哈哈哈

	Lleft(bst);				//再将其右旋
}

    4、右左型：先右旋，再左旋：

    老规矩，先贴图：
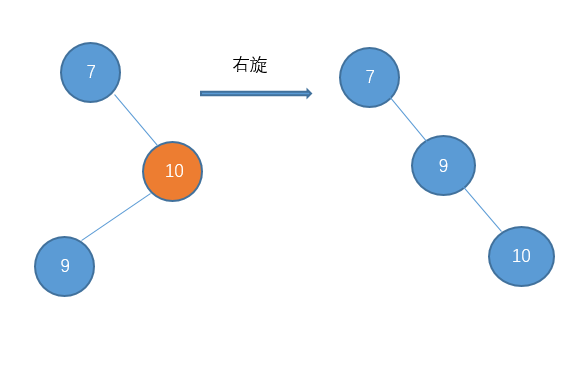
    在这里插入图片描述
    在这里插入图片描述

    代码实现：

    //右左型双旋转
void Rleft(BiTree &bst)
{
	//先做右旋，将其变成右右型
	BiTree rch = bst->rchild;
	BiTree rlch = bst->rchild->lchild;
	bst->rchild = rlch;
	bst->rchild->rchild = rch;
	bst->rchild->rchild->lchild = NULL;

	Rright(bst);				//再右旋
}

    实现重点来了

    我们每插入一个结点元素都要保证整棵树的每一个结点是平衡的，就要在插入这个结点后，从这个插入的结点往上逐个双亲结点去检查，看是否破坏了树的平衡，如果破坏了则对其进行左右旋转操作，保证其平衡性，直到树的根节点。

    因为树的递归性，在插入的时候是递归插入，

    按照栈的顺序，递归的过程中第一次递归的函数先入栈，以此类推，然后直到到达结束条件，前面的才依次出栈，

    所以可以在插入函数最后面使用检查每个结点的函数，出栈过程中，就可以沿着新插入结点一路回退检查每个双亲结点了。

    注意最后一行

    代码实现：

    //插入结点
void Insert_Binary_Tree(BiTree& bst ,int t)			//bst是根节点
{

	if (bst == NULL)	//空树或者叶结点
	{
		BiTree newp = new Binode;
		newp->data = t;
		newp->lchild = NULL;
		newp->rchild = NULL;
		bst = newp;	
	}
	else
	{
		if (t > bst->data)
			Insert_Binary_Tree(bst->rchild, t);
		else
			Insert_Binary_Tree(bst->lchild, t);
	}	
	//在最后检查这个结点，在递归的时候就可以将递归过程中从根节点往下的所有结点都检查了，按照出栈顺序，可以保证都是在插入后才依次向上检查的。
	Check_Binary_Tree(bst);		
}

    要实现这一功能就必须有一个检查是否平衡的依据———就是每个结点的左右子树的深度。这个函数是作为私有的对内接口。

    计算深度的实现：

    //一个结点的深度
int Binary_Tree_height(BiTree bst)		//bst为要计算的结点
{
	if (bst == NULL)
		return 0;
	int l = Binary_Tree_height(bst->lchild);
	int r = Binary_Tree_height(bst->rchild);
	return max(l, r) + 1;
}

    然后是一个检查这个结点是否平衡的函数，对外：

    检查平衡函数：

    //如果出现不平衡的情况就旋转
void Check_Binary_Tree(BiTree  &bst)		//bst为要检查的结点
{	
	if (bst == NULL)
		return;
	if (Binary_Tree_height(bst->lchild) - Binary_Tree_height(bst->rchild) > 1)
	{
		if (Binary_Tree_height(bst->lchild->lchild) > Binary_Tree_height(bst->lchild->rchild))
			Lleft(bst);
		else
			Lright(bst);
	}
	if (Binary_Tree_height(bst->rchild) - Binary_Tree_height(bst->lchild) > 1)
	{
		if (Binary_Tree_height(bst->rchild->rchild) > Binary_Tree_height(bst->rchild->lchild))
			Rright(bst);
		else
			Rleft(bst);
	}
}

    最后，对代码进行一下汇总：

    AVL.h文件

    #pragma once
#include<iostream>
constexpr auto ENDKEY = -1;
template<typename T1, typename T2>
constexpr auto max(T1 x, T2 y) { return x>y?x:y; }

using namespace std;

typedef struct Binary_Tree_node
{
	int data;	//数据域
	struct Binary_Tree_node* lchild, * rchild;		//左右孩子结点
}Binode, * BiTree;

//访问二叉树
void visit(int c, int level)
{
	printf("%d位于第%d层
", c, level);
}

//中序遍历
void Midorder_Traverse(BiTree T, int level)
{
	if (T)
	{
		Midorder_Traverse(T->lchild, level + 1);
		visit(T->data, level);
		Midorder_Traverse(T->rchild, level + 1);
	}
}

//一个结点的深度
int Binary_Tree_height(BiTree bst)
{
	if (bst == NULL)
		return 0;
	int l = Binary_Tree_height(bst->lchild);
	int r = Binary_Tree_height(bst->rchild);
	return max(l, r) + 1;
}

//遍历整棵树，如果出现不平衡的情况就旋转

//左左型单旋转
void Lleft(BiTree &bst)
{
	BiTree lch = bst->lchild;		//保存不平衡结点的左孩子结点
	bst->lchild = lch->rchild;
	lch->rchild = bst;
	bst = lch;
}

//右右型单旋转
void Rright(BiTree &bst)
{
	BiTree rch = bst->rchild;		//保存不平衡结点的右孩子结点
	bst->rchild = rch->lchild;
	rch->lchild = bst;
	bst = rch;
}

//左右型双旋转
void Lright(BiTree &bst)
{
	//先做左旋，将其变成左左型
	BiTree lch = bst->lchild;
	BiTree lrch = bst->lchild->rchild;
	bst->lchild = lrch;
	bst->lchild->lchild = lch;
	bst->lchild->lchild->rchild = NULL;		//可能存在bug	todo

	Lleft(bst);
}

//右左型双旋转
void Rleft(BiTree &bst)
{
	//先做右旋，将其变成右右型
	BiTree rch = bst->rchild;
	BiTree rlch = bst->rchild->lchild;
	bst->rchild = rlch;
	bst->rchild->rchild = rch;
	bst->rchild->rchild->lchild = NULL;

	Rright(bst);
}

void Check_Binary_Tree(BiTree  &bst)
{	
	if (bst == NULL)
		return;
	if (Binary_Tree_height(bst->lchild) - Binary_Tree_height(bst->rchild) > 1)
	{
		if (Binary_Tree_height(bst->lchild->lchild) > Binary_Tree_height(bst->lchild->rchild))
			Lleft(bst);
		else
			Lright(bst);
	}
	if (Binary_Tree_height(bst->rchild) - Binary_Tree_height(bst->lchild) > 1)
	{
		if (Binary_Tree_height(bst->rchild->rchild) > Binary_Tree_height(bst->rchild->lchild))
			Rright(bst);
		else
			Rleft(bst);
	}
	//Check_Binary_Tree(bst->lchild);
	//Check_Binary_Tree(bst->rchild);
}

//假设没有相等的data
//插入结点
void Insert_Binary_Tree(BiTree& bst ,int t)			//bst是根节点
{

	if (bst == NULL)	//空树或者叶结点
	{
		BiTree newp = new Binode;
		newp->data = t;
		newp->lchild = NULL;
		newp->rchild = NULL;
		bst = newp;	
	}
	else
	{
		if (t > bst->data)
			Insert_Binary_Tree(bst->rchild, t);
		else
			Insert_Binary_Tree(bst->lchild, t);
	}	
	Check_Binary_Tree(bst);
}

//创建一棵二叉排序树
BiTree Create_Binary_Tree()
{
	BiTree bst = NULL;
	int t;
	cin >> t;
	while (t != ENDKEY)
	{
		Insert_Binary_Tree(bst, t);
		cin >> t;
	}
	return bst;
}

//二叉排序树的删除
BiTree Delete_Binary_Tree(BiTree bst, int t)
{
	Binode* newp, * f, * s, * q;	
	newp = bst;
	f = NULL;
	while (newp)					
	{
		if (newp->data == t)
			break;
		f = newp;				
		if (t > newp->data)
			newp = newp->rchild;
		else
			newp = newp->lchild;
	}
	if (newp == NULL)				
		return bst;
	if (newp->lchild == NULL)
	{
		if (f == NULL)					
			 bst = bst->rchild;
		else if (f->lchild == newp)
			f->lchild = newp->rchild;
		else							
			f->rchild = newp->rchild;

		delete[]newp;			
	}
	else if (newp->rchild == NULL)		
	{
		if (f == NULL)
			bst = bst->lchild;
		else if (f->lchild == newp)
			f->lchild = newp->lchild;
		else
			f->rchild = newp->lchild;

		delete[]newp;
	}
	else				
	{
		q = newp;
		s = newp->lchild;
		while (s->rchild)
		{
			q = s;				
			s = s->rchild;		
		}
		if (q == newp)
			q->lchild = s->lchild;	
		else	
			q->rchild = s->lchild;
		newp->data = s->data;
		delete[]s;
	}
	Check_Binary_Tree(bst);
	return bst;
}

//搜索二叉树
BiTree Search_Binary_Tree(BiTree bst, int t)
{
	if (bst == NULL)
		return NULL;
	if (bst->data == t)
		return bst;
	else if (t > bst->data)
		return Search_Binary_Tree(bst->rchild, t);
	else
		return Search_Binary_Tree(bst->lchild, t);
}

    测试数据

    #include<iostream>
#include"BST.h"
using namespace std;
int main()
{
	BiTree bst = Create_Binary_Tree();
	int level = 1;
	Midorder_Traverse(bst, level);
	system("pause");
}

    测试结果:

    在这里插入图片描述
  • 相关阅读:
    【转载】Myeclipse如何自动创建hibernate
    win7 64位mysql安装及navicat 解压版
    NuGet套件还原步骤（以vs2012为例）
    Html.DropDownListFor() 二级联动 （$.getJSON）
    ModelState验证部分属性
    asp.net mvc发送邮件
    SpringBoot的热部署
    SpringBoot 入门demo
    集群、负载均衡、微服务、分布式的概念
    SpringBoot 简介
  • 原文地址：https://www.cnblogs.com/vfdxvffd/p/11694264.html
Copyright © 2020-2023  润新知