前提
void X_Sort ( ElementType A[], int N )
- 大多数情况下,为简单起见,讨论从小大的整数排序
- N是正整数
- 只讨论基于比较的排序(> = < 有定义)
- 只讨论内部排序(若内存小于数据大小,则需要外部排序)
- 稳定性:任意两个相等的数据,排序前后的相对位置不发生改变
- 没有一种排序是任何情况下都表现最好的
简单排序
冒泡排序
基础冒泡

- 从第1个泡泡开始,大的下沉,沉到不能沉为止,此时第n个泡泡最大。
- 从第i个泡泡开始,大的下沉,沉到不能沉为止,比较到n-i个泡泡即可。
void Bubble_Sort( ElementType A[], int N )
{ for ( P=N-1; P>=0; P-- ){
for( i=0; i<P; i++ ) { /* 一趟冒泡*/
if ( A[i] > A[i+1] ) {
Swap(A[i], A[i+1]);
}
}
}
}
加强版冒泡
- 用一个flag来标记,若一趟下来,不发生交换,则说明排序完成。
void Bubble_Sort( ElementType A[], int N )
{ for ( P=N-1; P>=0; P-- ){
flag = 0;
for( i=0; i<P; i++ ) { /* 一趟冒泡*/
if ( A[i] > A[i+1] ) {
Swap(A[i], A[i+1]);
flag = 1; /* 标识发生了交换*/
}
}
if ( flag==0 ) break; /* 全程无交换*/
}
}
优缺点分析
- 最好情况:顺序T = O( N )
- 最坏情况:逆序T = O( N^2 )
优点
- 易于实现
- 对数组 链表都没问题
- 稳定的
缺点
- 复杂度过高
插入排序
- 摸出第1张牌,从第n张开始比较,若大小关系错误,则第n张后移一位,再与n-1相比较,直到大小关系正确,插入该位置。
- 摸出第i张牌,从第n张开始比较,若大小关系错误,则第n张后移一位,再与n-1相比较,直到大小关系正确,插入该位置。
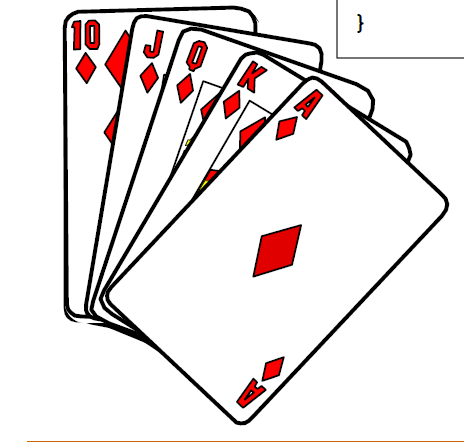
void Insertion_Sort( ElementType A[], int N )
{ for ( P=1; P<N; P++ ) {
Tmp = A[P]; /* 摸下一张牌*/
for ( i=P; i>0 && A[i-1]>Tmp; i-- )
A[i] = A[i-1]; /* 移出空位*/
A[i] = Tmp; /* 新牌落位*/
}
}
优缺点分析
最好情况:顺序T = O( N )
最坏情况:逆序T = O( N2 )
优点
- 易于实现
- 比冒泡好,每一步都少一些步骤
- 稳定的
缺点
- 复杂度高
插入排序的改进:希尔排序
- 定义增量序列 Dm>Dm-1>……>D1=1
- 对每个Dk进行“Dk-间隔”排序(K=m,m-1,……1)
- 注意:Dk间隔有序的序列,在执行“Dk-1间隔”排序后,仍然是Dk间隔有序的。
一个例子
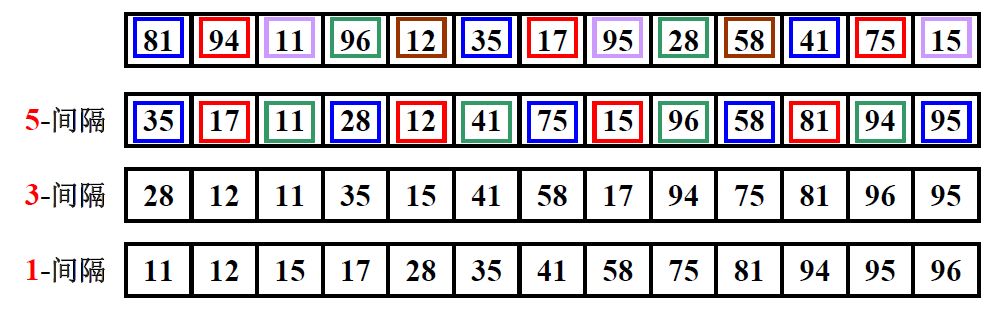
一个坏例子
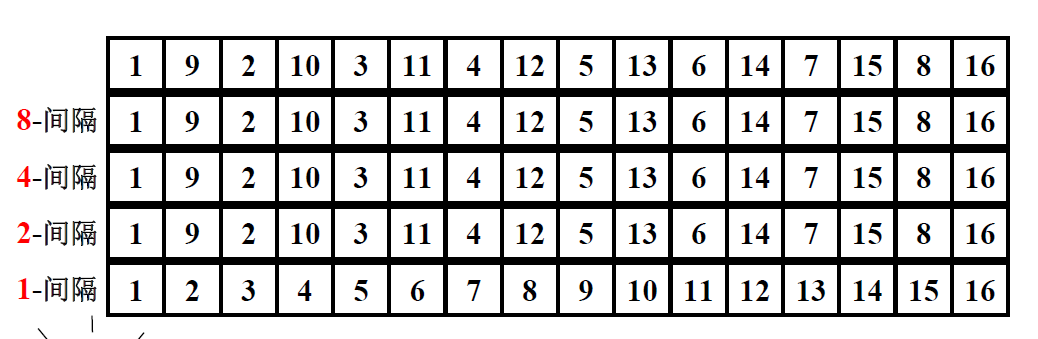
- 原始希尔排序DM = 向下取整( N / 2 ) , Dk = 向下取整( Dk+1 / 2 )。
- 最坏情况: T = θ( N2 )
void Shell_sort( ElementType A[], int N )
{ for ( D=N/2; D>0; D/=2 ) { /* 希尔增量序列*/
for ( P=D; P<N; P++ ) { /* 插入排序*/
Tmp = A[P];
for ( i=P; i>=D && A[i-D]>Tmp; i-=D )
A[i] = A[i-D];
A[i] = Tmp;
}
}
}
更多增量序列

基于比较的排序
时间复杂度下界
- 对于下标i<j,如果A[i]>A[j],则称(i,j)是
一对逆序对(inversion) - 问题:序列{34, 8, 64, 51, 32, 21}中有多少逆序对?
- (34, 8) (34, 32) (34, 21) (64, 51) (64, 32) (64, 21) (51, 32) (51, 21) (32, 21)
- 交换2个相邻元素正好消去1个逆序对!
- 插入排序:T(N, I) = O( N+I )
- 如果序列基本有序,则插入排序简单且高效
相关定理
- 定理:任意N个不同元素组成的序列平均具有
N ( N - 1 ) / 4 个逆序对。 - 定理:任何仅以交换相邻两元素来排序的算
法,其平均时间复杂度为Ω ( N2 ) 。 - 这意味着:要提高算法效率,我们必须每次消去不止1个逆序对!
- 每次交换相隔较远的2个元素!