【DSU on tree】树上启发式合并入门

dsu on tree 树上启发式合并

题目

U41492 树上数颜色

给出一颗根为 \(1\) 的树，每次询问子树颜色种类数

暴力统计

直接暴力统计每颗子树的颜色种类。

按理说这是一道 dsu on tree 的模板题目，但是竟然直接暴力过掉了

暴力方法：

首先向下 DFS，算儿子节点的答案，递归后来后，再次向下 DFS 计算当前子树的答案。

当前子树 DFS 结束后，删除当前子树的影响，避免影响其他节点。

部分代码：

int ans;
void cal(int u, int fa, int type)//统计答案 或 消除影响
{
    num[val[u]] += type;
    if (type == 1 && num[val[u]] == 1) {
        ans++;
    }
    if (type == -1 && num[val[u]] == 0) {
        ans--;
    }
    for (int i = 0; i < vec[u].size(); i++) {
        int v = vec[u][i];
        if (v == fa)
            continue;
        cal(v, u, type);
    }
}
void dfs2(int u, int fa)
{
    for (int i = 0; i < vec[u].size(); i++) {//先算儿子节点的答案
        int v = vec[u][i];
        if (v == fa)
            continue;
        dfs2(v, u);
    }
    //递归回来后，不会受其他节点的影响，下面消除了影响
    num[val[u]]++;//更新当前节点的颜色
    if (num[val[u]] == 1)
        ans++;
    for (int i = 0; i < vec[u].size(); i++) {//向下递归计算答案
        int v = vec[u][i];
        if (v == fa)
            continue;
        cal(v, u, 1);
    }
    rel[u] = ans;
    cal(u, fa, -1);//消除根节点为 u 的子树的影响
}

优化

上面的代码中，每颗子树遍历完之后，都清空了自身的影响。

而最后遍历的一颗子树没有必要清空。

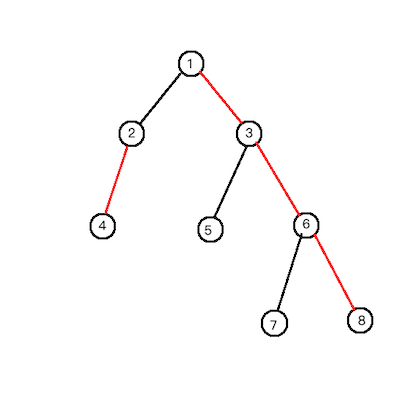
比如对于 1 节点，最后遍历的子树为 3 。

这时我们清空了 3 5 6 7 8节点的颜色值。

回到了节点 1。

接下来又会向下遍历统计节点 1 的答案。把2 4 3 5 6 7 8 更新了进去。

那么子树 3 就没有必要被清空，如果没被清空,统计答案时只需再遍历2 4两个节点。

为了使得统计答案时遍历的节点更少，我们肯定最后访问最大的那颗子树。(即树链剖分中的重儿子)

算法实现

递归计算所有轻儿子，递归结束时它们没有贡献
递归计算重儿子，递归结束时保留贡献
计算当前子树轻儿子的贡献
更新答案
如果当前子树的根节点是轻儿子，消除当前子树的贡献

代码

#include <algorithm>
#include <iostream>
#include <map>
#include <math.h>
#include <queue>
#include <set>
#include <stack>
#include <stdio.h>
#include <string.h>
#include <string>
#include <vector>
#define emplace_back push_back
#define pb push_back
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int mod = 1e9 + 7;
const int seed = 12289;
const double eps = 1e-6;
const int inf = 0x3f3f3f3f;
const int N = 2e5 + 10;

vector<int> vec[N];
int val[N], son[N], sz[N], num[N], rel[N], ans;
void dfs1(int u, int fa)//得到重儿子
{
    sz[u] = 1;
    for (auto v : vec[u]) {
        if (v == fa)
            continue;
        dfs1(v, u);
        sz[u] += sz[v];
        if (sz[v] > sz[son[u]])
            son[u] = v;
    }
}
void cal(int u, int fa, int type)//计算贡献 或 消除影响
{
    num[val[u]] += type;
    if (num[val[u]] == 1 && type == 1) {
        ans++;
    }
    if (num[val[u]] == 0 && type == -1) {
        ans--;
    }
    for (auto v : vec[u]) {
        if (v != fa)
            cal(v, u, type);
    }
}
void dfs2(int u, int fa, int type)
{
    for (auto v : vec[u]) {//向下递归计算轻儿子的答案
        if (v != fa && v != son[u])
            dfs2(v, u, -1);//-1 表示递归结束清除子树影响
    }
    if (son[u])//递归重儿子，保留影响
        dfs2(son[u], u, 1);
    num[val[u]]++;//计算根节点的影响
    if (num[val[u]] == 1)
        ans++;
    for (auto v : vec[u]) {//统计轻儿子的贡献
        if (v != fa && v != son[u])
            cal(v, u, 1);
    }
    rel[u] = ans;//更新答案
    if (type == -1)//是否消除当前子树的影响
        cal(u, fa, -1);
}
int main()
{
    int n;
    scanf("%d", &n);
    for (int i = 1; i < n; ++i) {
        int u, v;
        scanf("%d%d", &u, &v);
        vec[u].pb(v), vec[v].pb(u);
    }
    for (int i = 1; i <= n; ++i) {
        scanf("%d", &val[i]);
    }
    dfs1(1, 0);
    dfs2(1, 0, 1);
    int m;
    scanf("%d", &m);
    while (m--) {
        int x;
        scanf("%d", &x);
        printf("%d\n", rel[x]);
    }
    return 0;
}

几道题目：

E. Lomsat gelral

题目链接

求每个子树的上的众数和。

定义 sum 表示众数和，maxn 表示目前众数的出现次数，使用num[] 维护数字出现的数量。

只要搞清楚何时将 sum 以及 maxn 赋值为 0 ，这道题就简单了。

当当前子树的根节点为轻儿子时，因为要清空整个子树，所以 maxn 和 sum 需要清空。

代码

#include <algorithm>
#include <iostream>
#include <map>
#include <math.h>
#include <queue>
#include <set>
#include <stack>
#include <stdio.h>
#include <string.h>
#include <string>
#include <vector>
#define emplace_back push_back
#define pb push_back
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int mod = 1e9 + 7;
const int seed = 12289;
const double eps = 1e-6;
const int inf = 0x3f3f3f3f;
const int N = 1e5 + 10;

vector<int> vec[N];
int val[N], son[N], sz[N], num[N];
ll rel[N];
void dfs1(int u, int fa)
{
    sz[u] = 1;
    for (auto v : vec[u]) {
        if (v == fa)
            continue;
        dfs1(v, u);
        sz[u] += sz[v];
        if (sz[v] > sz[son[u]])
            son[u] = v;
    }
}

int maxn;
ll sum;

void cal(int u, int fa, int type)
{
    num[val[u]] += type;
    if (num[val[u]] > maxn) {
        maxn = num[val[u]];
        sum = val[u];
    } else if (num[val[u]] == maxn) {
        sum += val[u];
    }
    for (int i = 0; i < vec[u].size(); i++) {
        int v = vec[u][i];
        if (v != fa)
            cal(v, u, type);
    }
}

void dfs2(int u, int fa, int type)
{
    for (int i = 0; i < vec[u].size(); i++) {
        int v = vec[u][i];
        if (v != fa && v != son[u])
            dfs2(v, u, -1);
    }
    if (son[u])
        dfs2(son[u], u, 1);
    for (int i = 0; i < vec[u].size(); i++) {
        int v = vec[u][i];
        if (v != fa && v != son[u])
            cal(v, u, 1);
    }
    num[val[u]]++;
    if (num[val[u]] > maxn) {
        maxn = num[val[u]];
        sum = val[u];
    } else if (num[val[u]] == maxn) {
        sum += val[u];
    }
    rel[u] = sum;
    if (type == -1) {
        cal(u, fa, -1);
        sum = 0, maxn = 0;
    }
}

int main()
{
    int n;
    scanf("%d", &n);
    for (int i = 1; i <= n; ++i) {
        scanf("%d", &val[i]);
    }
    for (int i = 1; i < n; ++i) {
        int u, v;
        scanf("%d%d", &u, &v);
        vec[u].pb(v), vec[v].pb(u);
    }
    dfs1(1, 0);
    dfs2(1, 0, 1);
    for (int i = 1; i <= n; i++) {
        printf("%lld ", rel[i]);
    }
    printf("\n");
    return 0;
}

F.Strange Memory

题目链接

给出一颗有权树，求:

\[\sum\limits_{i=1}^n\sum\limits_{j=i+1}^n [a_i \oplus a_j = a_{\operatorname{lca}(i, j)}] (i \oplus j). \]

\(1 \leq a_i \leq 10^6\)

牵扯到异或，十有八九要拆位。

由异或的性质知如果 \(a \oplus b =c\)，那么\(a \oplus c =b，b \oplus c =a\)

即知道 \(lca\) 的权值以及其中一个节点的权值就能知道另外一个权值。

枚举每个节点作为 \(lca\) 时对答案产生的贡献。

显然，\(i\) 和 \(j\) 一定不在 \(lca(i,j)\) 的同一颗子树中。

我们遍历 \(lca\) 的子树，枚举每个节点作为 \(j\) 时产生的贡献。

此时可以知道\(a_i\) 的值应为 \(a_j \oplus a_{lca(i,j)}\) ，

我们维护值为 \(a_i\) 的都有哪些节点。

那么当前节点 \(u\)作为 \(j\) 的贡献值为 \(\sum v_{权值为a_i} \oplus u\)

如果直接遍历一遍求和，复杂度太高。

我们可以对每个权值维护一个二进制数组 \(num[i][j]\) 表示已经出现过的权值为 \(i\) 的第 \(j\) 位为 1 的个数。

再维护每个权值出现的次数 \(num2[i]\)。

我们求贡献的时候只需要遍历 \(u\) 的前 \(18\) 位，如果第 \(x\) 位为 0 ，答案加上 \(2^x \times num[a_i][x]\) ，否则加上 \(2^x \times (num2[a_i]-num[a_i][x])\)

当求完一颗子树的贡献后，将这颗子树上所有的节点更新到 \(num,num2\)数组中。

#include <algorithm>
#include <iostream>
#include <map>
#include <math.h>
#include <queue>
#include <set>
#include <stack>
#include <stdio.h>
#include <string.h>
#include <string>
#include <vector>
#define emplace_back push_back
#define pb push_back
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int mod = 1e9 + 7;
const int seed = 12289;
const double eps = 1e-6;
const int inf = 0x3f3f3f3f;
const int N = 1e5 + 10;

vector<int> vec[N];
int val[N], son[N], sz[N];
int num[N * 20][18], num2[N * 20];
void dfs1(int u, int fa)
{
    sz[u] = 1;
    for (auto v : vec[u]) {
        if (v == fa)
            continue;
        dfs1(v, u);
        sz[u] += sz[v];
        if (sz[v] > sz[son[u]])
            son[u] = v;
    }
}
vector<int> tmp;
ll ans;
void cal(int u, int fa, int rt, int type)
{
    if (type == 1) {//计算答案
        int now = val[u] ^ val[rt];
        for (int i = 0; i < 18; i++) {
            if ((1 << i) & u) {
                ans += 1LL * (num2[now] - num[now][i]) * (1 << i);
            } else {
                ans += 1LL * num[now][i] * (1 << i);
            }
        }
        tmp.pb(u);//跑完当前子树要更新进去，所以先放到一个vector中
    } else {//撤销影响
        num2[val[u]]--;
        for (int i = 0; i < 18; i++) {
            if ((1 << i) & u) {
                num[val[u]][i]--;
            }
        }
    }
    for (int i = 0; i < vec[u].size(); i++) {
        int v = vec[u][i];
        if (v != fa)
            cal(v, u, rt, type);
    }
}

void dfs2(int u, int fa, int type)
{
    for (int i = 0; i < vec[u].size(); i++) {
        int v = vec[u][i];
        if (v != fa && v != son[u])
            dfs2(v, u, -1);
    }
    if (son[u])
        dfs2(son[u], u, 1);
    num2[val[u]]++;
    for (int i = 0; i < 18; i++) {
        if ((1 << i) & u) {
            num[val[u]][i]++;
        }
    }
    for (int i = 0; i < vec[u].size(); i++) {
        int v = vec[u][i];
        if (v != son[u] && v != fa) {
            tmp.clear();
            cal(v, u, u, 1);
            for (int j = 0; j < tmp.size(); j++) {//遍历完更新当前子树的节点
                num2[val[tmp[j]]]++;
                for (int k = 0; k < 25; k++) {
                    if ((1 << k) & tmp[j]) {
                        num[val[tmp[j]]][k]++;
                    }
                }
            }
        }
    }
    if (type == -1) {
        cal(u, fa, fa, -1);
    }
}

int main()
{
    int n;
    scanf("%d", &n);
    for (int i = 1; i <= n; ++i) {
        scanf("%d", &val[i]);
    }
    for (int i = 1; i < n; ++i) {
        int u, v;
        scanf("%d%d", &u, &v);
        vec[u].pb(v), vec[v].pb(u);
    }
    dfs1(1, 0);
    dfs2(1, 1, 1);
    printf("%lld\n", ans);
    return 0;
}

相关阅读:
100——第9例
 100——第8例
 100——第7例
 POJ
POJ
POJ
Egyptian Collegiate Programming Contest 2017 (ACM ECPC 2017)
SCUT
SCUT
SCUT
原文地址：https://www.cnblogs.com/valk3/p/13965064.html

热门文章
牛牛爱学习
 P1024 一元三次方程求解
 P1873 砍树
 P1102 A-B 数对
 100——第15例
 100——第14例
 100——第13例
 100——第12例
 100——第11例
 100——第10例

【DSU on tree】树上启发式合并 入门