矩阵乘法及矩阵快速幂
定义:由 m × n 个数aij排成的m行n列的数表称为m行n列的矩阵,简称m × n矩阵。记作:
这m×n 个数称为矩阵A的元素,简称为元,数aij位于矩阵A的第i行第j列,称为矩阵A的(i,j)元,以数 aij为(i,j)元的矩阵可记为(aij)或(aij)m × n,m×n矩阵A也记作Amn。
元素是实数的矩阵称为实矩阵,元素是复数的矩阵称为复矩阵。而行数与列数都等于n的矩阵称为n阶矩阵或n阶方阵 。
基本算法:
加法/减法:用于同型矩阵,不同矩阵的相同位置相加减
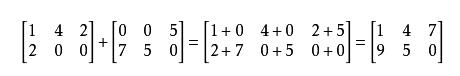
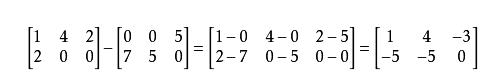
数乘:矩阵中的每一个数乘那个数,得到新的矩阵
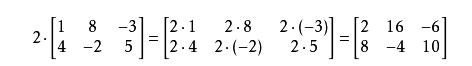
矩阵的加、减、数乘合称矩阵的线性运算(好像跟向量的加、减、数乘差不多)
转置:把矩阵A的行和列互相交换所产生的矩阵称为A的转置矩阵,这一过程称为矩阵的转置

矩阵的转置满足以下运算律:

共轭:矩阵的共轭定义为:![]() .一个2×2复数矩阵的共轭如下所示:
.一个2×2复数矩阵的共轭如下所示: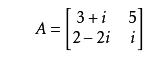 则
则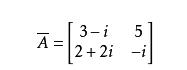
共轭转置:矩阵的共轭转置定义为:![]() ,也可以写为:
,也可以写为:![]() 。一个2×2复数矩阵的共轭如下所示:
。一个2×2复数矩阵的共轭如下所示: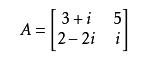 则
则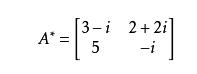
乘法:两个矩阵的乘法仅当第一个矩阵A的列数和另一个矩阵B的行数相等时才能定义。如A是m×n矩阵和B是n×p矩阵,它们的乘积C是一个m×p矩阵![]() ,它的一个元素:
,它的一个元素:![]() 并将此乘积记为:
并将此乘积记为:![]()
满足的运算律: 结合律:A*(B*C) = (A*B)*C
分配律:A*(B+C) = A*B+A*C
分配律若满足(A+B)*C,则不满足C*(A+B)
(矩阵乘法不满足交换律)
矩阵乘法证明过程参考:http://www.ruanyifeng.com/blog/2015/09/matrix-multiplication.html
接下来,放代码:
#include<algorithm> #include<iostream> #include<cstring> #include<cstdio> #define M 5005 using namespace std; int n, m, l, p; int a[M][M], b[M][M]; int c[M][M]; void add() { //矩阵a、b应为同型矩阵 for(int i = 1; i <= n; i++) for(int j = 1; j <= n; j++) c[i][j] = a[i][j] + b[i][j]; //减法只需将‘+’改为‘-’ } void mul() { //矩阵乘法 for(int i = 1; i <= n; ++i) for(int k = 1; k <= m; ++k) { int r = a[i][k]; for(int j = 1; j <= l; ++j) c[i][j] += r * b[k][j]; } /* 另一种写法 若把三重循环中的i,j,k枚举顺序交换,速度可能慢几倍 for(int i=1;i<=h;i++) for(int j=1;j<=l;j++) for(int k=1;k<=ll;k++) c[i][k] += a[i][j] * b[j][k]; */ } // 矩阵快速幂 struct Mat { ll m[101][101]; } a, e; Mat Mul(Mat x, Mat y) { Mat c; for (int i = 1; i <= n; ++i) for (int j = 1; j <= n; ++j) c.m[i][j] = 0; for (int i = 1; i <= n; ++i) for (int j = 1; j <= n; ++j) for (int k = 1; k <= n; ++k) c.m[i][j] = c.m[i][j] % mod + x.m[i][k] * y.m[k][j] % mod; return c; } Mat pow(Mat x, ll y) { Mat ans = e; while (y) { if (y & 1) ans = Mul(ans, x); x = Mul(x, x); y >>= 1; } return ans; } // int main() { scanf("%d%d%d", &n, &m, &l); /* 输入 */ return 0; }