二叉查找树(也叫二叉搜索树)是二叉树的一种,其特点是根节点比左孩子大,比右孩子小,在查找相应值的场景下非常有用。
那为什么需要二叉查找树,查找不是可以使用有序数组或者链表的数据结构吗?能问出这个问题的读者,想必也知道,有序数组搜索的时间复杂度是O(lg n),缺点在于插入和删除的时间复杂度是O(n);链表结构搜索的时间复杂度是O(n),在已知节点位置的前提下,插入和删除的时间复杂度是O(1),否则仍然是O(n)。二叉查找树就是为了要弥补这两种数据结构的缺点而创建的数据结构,粘贴一个二叉搜索树的图片,先观察一下。
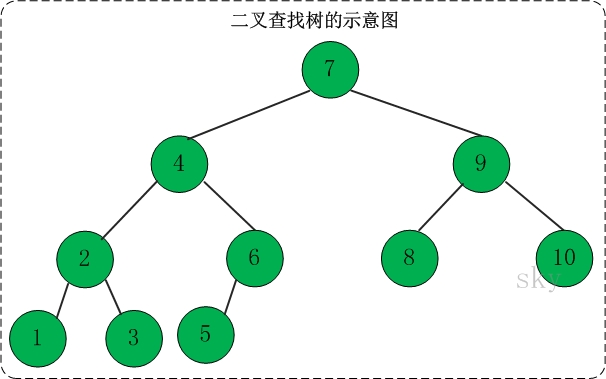
实际上,二叉搜索树是一种有序的链式结构,其搜索和插入删除的时间复杂度是相同的。最好的情况,是二叉树是比较平衡的,高度在lg n 数量级,其搜索和插入的时间复杂度也是O(lg n);最坏的情况是,二叉树完全不平衡,其高度是n,这样的二叉树叫偏斜树,放个图看下,下图第二第三个树就是这样的偏斜树。
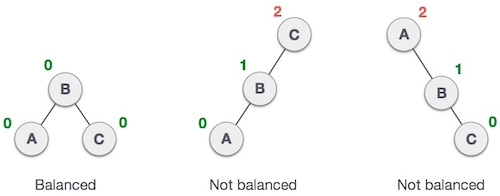
怎么样让二叉树节点平衡,我们下一节继续研究,本节主要说明二叉搜索树的一些操作。在说明二叉搜索树的基本操作之前,要思考一个问题,给定一串数字,这些数字构成的二叉搜索数是唯一的吗?
脑袋转的快的同学已经反应过来了,当然不唯一,不同的数字作根节点构建的树自然不相同,但它们都满足二叉搜索树的性质。这个,读者可以自己举个例子试一试。好了,开始正文。
- 搜索。 二叉查找树的搜索比较容易,就是从根开始依次比较,直到叶子节点,返回成功或者失败的节点。
- 插入。 二叉查找树的插入也不难,插入自然需要知道插入的位置,这里要调用搜索操作。如果节点已经存在,返回error,否则返回的结果为其要插入的节点,且该节点必为叶子。如果不是叶子,搜索就会继续往下进行。
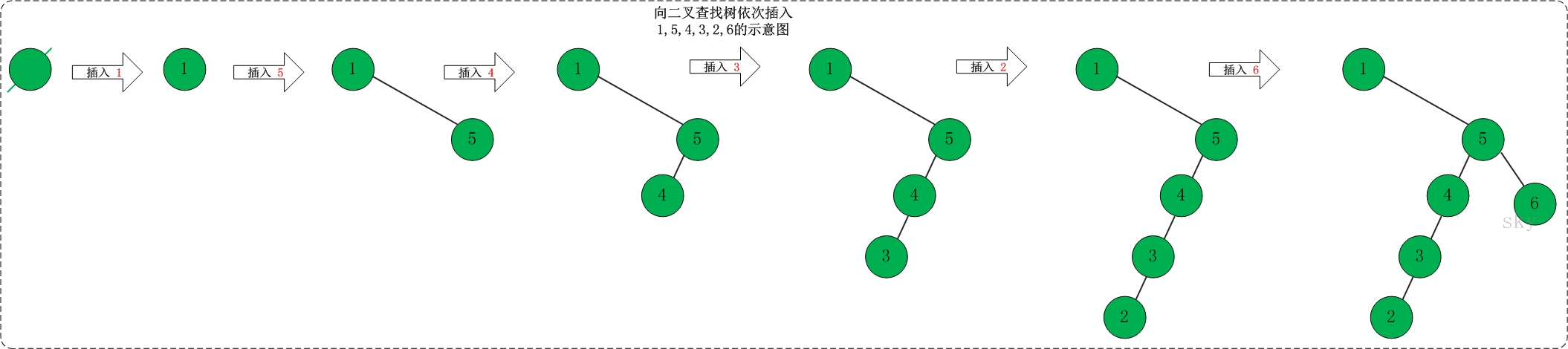
- 删除。删除相对插入就要复杂一些,因为插入的节点必为叶子,而删除的节点除了叶子之外还有非叶子节点。非叶子节点又可能有一个或两个孩子,这时候该怎么删除?
- 叶子节点的情况。直接删除,没有什么好说的。
- 非叶子节点且有一个孩子。删除节点,并将原节点的孩子粘贴到原来父节点的相应子树上。
- 非叶子节点且有两个孩子。两个孩子怎么办?原来节点父节点只能保证空出来一个子树连接,直接删除,那删除节点的另一个子树该放在什么位置?
针对第三种情况,当然不能直接删除。这时候要思考一下,有没有好的办法?还记得之前咱们说过的吗,即使是同一串数列,也会有很多种二叉查找树,能不能用这个性质做点什么?放一张图: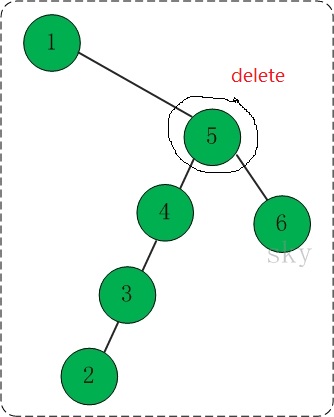
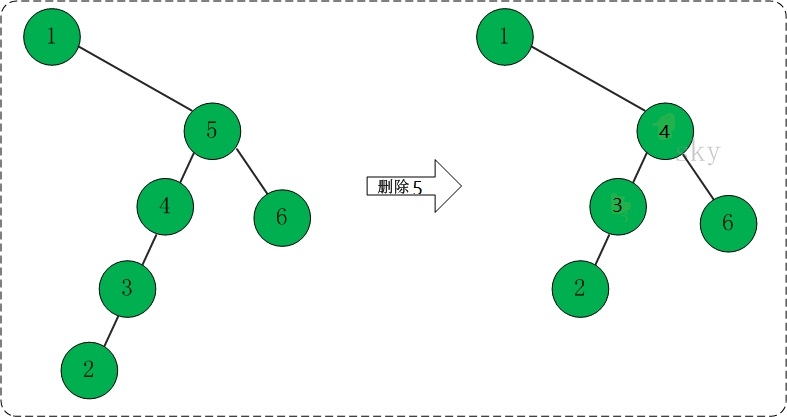
如上左图,要删除节点5,我们要保证删除后的树依旧是二叉查找树,也即根节点比左孩子大,比右孩子小,至于删除后的树是不是和原来的树的节点位置是否一样,那不重要。根据二叉查找树的特点,其中序遍历的输出结果一定是有序的。发现被删除节点虽然有两个孩子,但是在原来的树中,其前趋/后继节点,肯定没有右孩子/左孩子。如果有的话,那么就不可能成为删除节点的前趋/后继。如上图,5节点中序遍历的前趋是4,后继是6。
这里要考虑一个问题,怎么找到节点的前趋/后继节点,这个问题不难。节点的前趋可能要上行,也可能在其左子树中。有兴趣的同学可以思考一下,寻找后继与前趋是相同的问题,或者说对称的问题,考虑清楚前趋,后继寻找也就不难了。节点的前趋,如果节点有左子树,那肯定在左子树上,如果没有,那就是其父节点。
好了,在情况3中,节点有两个孩子,所以其前趋在左子树中,具体怎么找就不赘述了。在上例中,5的前趋是4。
找到前趋之后干什么?用前趋替代被删除的节点,然后问题就变成了如何删除原节点的前趋,这个问题就是情况1和情况2讨论的问题,删除问题得解!
具体的实现代码会在下节AVL平衡树中给出,谢谢!