4247 奇特的生物
时间限制: 1 s
空间限制: 128000 KB
题目等级 : 钻石 Diamond
题解
题目描述 Description
科学家们最近发现了一种奇怪的生物,它们每天长大一岁,刚出生的宝宝为1岁,且它们的年龄没有上限。已知年龄为1岁,2岁,3岁,……,k岁的个体具有生育能力,当年龄为i的具有生育能力的个体将长大一岁时会生下ai个1岁的幼崽。假设第一天只有一个年龄为1的幼崽,现在科学家们想知道第x天年龄为y的个体有多少,但由于该物种增长速度太快,于是他们将这个任务交给了你。由于这个数可能很大,你需要对p取模。
输入描述 Input Description
输入数据第一行给定四个整数k,x,y,p。
第二行包括k个整数,第i个整数代表ai。
输出描述 Output Description
输出数据包含一行,表示第x天年龄为y的个体的数量对p取模后的结果。
样例输入 Sample Input
【样例输入 1】
3 3 1 1007
1 1 1
【样例输入 2】
3 6 2 1007
1 2 1
样例输出 Sample Output
【样例输出1】
2
【样例输出 2】
13
增加一个新样例。codevs上的第十个点。
莫名其妙的矩阵快速幂解决不了。
样例输入3:
10 10258496531232 52 700000000017
5 89 63 25 48 76 95 23 15 25
样例输出3:
611559827774
分析:
这道题轻轻一想发现。哦。可以用递推来模拟。递推公式大致应该是这个样子的。
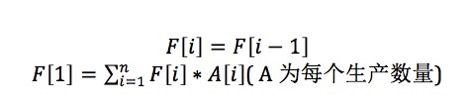
由题意可知。每个年龄的数量都是由上个年龄的人长成这个年龄的。而只有1岁的人是靠1-k有生育能力的人生产出来的。
由于这个范围很大。所以很容易让人想到用矩阵乘法来对这个进行递推优化。
但是仔细一想。发现这道题有个性质。就是没个人数都是由上一个转化过来的,那么。其实当F[1]产生的时候。以后的数量就是确定的。所以我们就没必要把全部的情况都存下来。就存1-k,每次进行状态转移就好。其次我们会发现。在整个序列里。因为只有F[1]在变所以我们求 x天y岁人数的问题就转换成了。我们求 x-y+1天1岁的人数问题。为什么呢?。我们y岁人数起时在底x-y+1天就转化好了。而之后剩下的天数,就是将x-y+1天1岁的人转移转移到x天y岁。
接下来的问题就剩到了,如何建立矩阵之后用矩阵来快速幂一些奇怪的事情。

这个矩阵很显然易见的解决这个问题。因为矩阵乘法是第一个举证的行乘第二个的列。所以我们在这里矩阵A第一行就是将F[1~k]里的所有结果相加。之后的行就完成了一个转移的工作。将上一天转换到当前天数。
于是就是将整个矩阵乘上 x-y 次。求A[1][1]--代表第x-y+1天的一岁的人数。
还有既然都是乘x-y次那么我们就要对(y>x)的情况进行特判。还有就是要加上快速乘法。不然第10个点过不去。这个数据就专门来卡你。
贴上代码。
#include<cstdio>
#include<algorithm>
#include<string.h>
using namespace std;
long long int mod,k,x,y;
struct node{
long long l[100][100];
node()
{
memset(l,0,sizeof(l));
}
}a,ans;
long long mul(long long x, long long y) {
long long ret = 0;
for(; y; y >>= 1) {
if((y & 1) && (ret += x) >= mod) ret -= mod;
if((x <<= 1) >= mod) x -= mod;
}
return ret;
}
node operator*(node a,node b)
{
node res;
for(int i=1;i<=k;++i)
for(int j=1;j<=k;++j)
{
for(int q=1;q<=k;++q)
{
res.l[i][j] += mul(a.l[i][q], b.l[q][j]);
if(res.l[i][j] >= mod) res.l[i][j] -= mod;
}
}
return res;
}
int main()
{
scanf("%lld%lld%lld%lld",&k,&x,&y,&mod);
for(long long int i=1;i<=k;++i)
{
scanf("%lld",&a.l[1][i]);
a.l[i+1][i]=1;
ans.l[i][i]=1;
}
if(x<y){
printf("0");
return 0;
}
for(long long int i=x-y;i!=0;i>>=1 ,a=a*a)
{
if(i&1)ans=a*ans;
}
printf("%lld",ans.l[1][1]);
return 0;
}