1,矩阵
矩阵这个东西。顾名思义。就是由元素组成的矩形阵列。如图。这里的元素可能是符号啊,实数,式子什么的。
而这个矩阵的意义其实在于求解线性方程组。线性方程组中的未知数的量排成一个矩阵,加上常数项,就是增广矩阵。
还有什么表示线性转换,就不讲了。反正。也不会。

2,标记。
一般将一个矩阵中的m*n个元素,简称元,数a(ij)的位于矩阵A的第i行,第j列。这个数就被叫做这个矩阵A的(i,j)元。各种的记法就不说了。都是一个东西。明白元。就好。之后就是矩阵是怎么来的。
其实矩阵一开始是用来表示线性方程组。就像上面讲的一样。给一个图式可能就会明白很多。

就是这样,在求解线性方程和快速优化DP方程组的时候都特别有用。矩阵快速幂--就是很强大。
3,矩阵的基本运算。
这个相比于矩阵乘法就很简单了,简单明了,https://zh.wikipedia.org/wiki/矩阵 这个维基百科讲的很详细,我就简单讲讲。
1)加减法,矩阵做加法的时候,得满足两个矩阵都是m*n的范围。所以。每一位对应相加就好了。
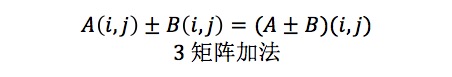

矩阵的加减法满足结合律和交换律。(重点)
2)数乘,注意这里不是乘法,只是数乘,用一个数,去乘矩阵里的每一个数。

矩阵的数乘满足结合律和分配律。
3)转置,矩阵的转置,就是把矩阵A的行换成同序数的列所得到的新矩阵。简单来讲。就是


4,关于矩阵乘法。
这个才是矩阵的重头戏。才是精髓,矩阵被定义出来求解线性方程,这个就是重头戏。
首先,矩阵乘法中,两矩阵必须满足 矩阵A mn 矩阵B nq 矩阵A的列数必须等于矩阵B的行数。他们的乘积求出的矩阵C 就是矩阵m*q。

给出一个矩阵乘法公式。

矩阵乘法主要满足结合律和左分配律和右分配律。但是!就是不满足交换律。
关于证明,这个很玄学。很多省队的dalao都会。这里贴上室友的博客,他写的是可以看懂,不过证明的不全,这个东西,知其意就好。
http://www.cnblogs.com/reddest/p/5919686.html
5,斐波那契数列,矩阵乘法算法。
斐波那契数列的递推式很简单 f[i]=f[i-1]+f[i-2]
这个也可以看成一个线性方程,如果,把f[i-1] ,f[i-2]看成未知数,而f[i]看成他们的函数值。这里,线性方程就有了。可是这知识一个啊。没有线性方程组。,方程组这个东西可以凑,这个可以自己组合起来,而这个构造矩阵模型,就是矩阵最难的地方,这个得自己去推算,和证明。
贴上我的方法。

既然知道方法,其实代码实现就很简单了。这里放一个简单的斐波那契数列的代码。
1 #include<cstdio> 2 #include<string.h> 3 struct node { 4 long long int v[3][3]; 5 node(){ 6 memset(v,0,sizeof(v)); 7 } 8 }a,ans; 9 int mod; 10 node operator*(node x,node y)//重载运算符,这里模拟的是矩阵乘法。 11 { 12 node res; 13 for(int i=1;i<=2;++i) 14 for(int j=1;j<=2;++j) 15 for(int k=1;k<=2;++k) 16 { 17 res.v[i][j]+=(x.v[i][k]*y.v[k][j]); 18 } 19 return res; 20 } 21 int main() 22 { 23 int n,t; 24 scanf("%d",&n); 25 while(n--) 26 { 27 ans.v[1][1]=1;ans.v[2][1]=1;//初始化初始矩阵1。 28 a.v[1][1]=a.v[1][2]=a.v[2][1]=1; 29 scanf("%d",&t); 30 for(int i=1;i<t-2;i++) //注意理解乘方的概念。 31 { 32 ans=a*ans; 33 } 34 printf("%lld ",ans.v[1][1]); 35 } 36 return 0; 37 }
6,矩阵快速幂。
这个其实是快速幂的主要思路。不过乘法代替成矩阵乘法.
1 #include<cstdio> 2 #include<string.h> 3 struct node{ 4 int v[3][3]; 5 node(){ 6 memset(v,0,sizeof(v)); 7 } 8 }ans,a; 9 node operator*(node x,node y) 10 { 11 node res; 12 for(int i=1;i<=2;++i) 13 for(int j=1;j<=2;++j) 14 { 15 for(int k=1;k<=2;k++) 16 res.v[i][j]+=(x.v[i][k]*y.v[k][j]); 17 } 18 return res; 19 } 20 int main() 21 { 22 int n; 23 scanf("%d",&n); 24 a.v[1][1]=a.v[1][2]=a.v[2][1]=1; 25 ans.v[1][1]=1;ans.v[2][2]=1; 26 for(int i=n-1;i;i>>=1,a=a*a) 27 { 28 if(i&1)ans=ans*a; 29 } 30 printf("%d",ans.v[1][1]); 31 return 0; 32 }