关于拓扑排序:
以下拓扑排序的内容,只适合于AOV网。简单来说就是有向无环图。
1)举一个简单明了的栗子。(网上大部分都是这个栗子)
“选课”
比如说。我想选修课程B,但是我必须先选修课程A。选课程A之前。还得选修课程C。这就自然形成了一个简单的图。
C-》A-》B
只有选完c。才能说a的事情。选完a才能提选b的事情。
发现这里。要先完成的事情。必须要比后完成的事情提前完成(这是人之常情)。
而拓扑排序的作用呢。就是将一个有向图。压缩成一个线性的序列。使得先要完成的在前面。后完成的总在先完成的后面。
这里提几个专有名词。
前驱活动:我们把一条有向边的起点活动称为终点活动的前驱活动(例如c是a的前驱活动)。
后驱活动:同理把一条有向边的终点活动称为起点活动的后驱活动(例如a是c的后驱活动)。
而拓扑排序出来的线性的序列,叫拓扑序列。(hhhhh这个名字很裸)
构造拓扑序列可以帮助我们合理安排一个工程的进度。由AOV网构造拓扑序列具有很高的实际应用价值。
2)举一个复杂的大栗子。
“选课2”
比如说。我想选修B。但是我必须选修课程A。选修课程A。之前还得选修课程C和课程D。选修课程D必须选修课程F。
画出来就是这个样子:(有点丑)
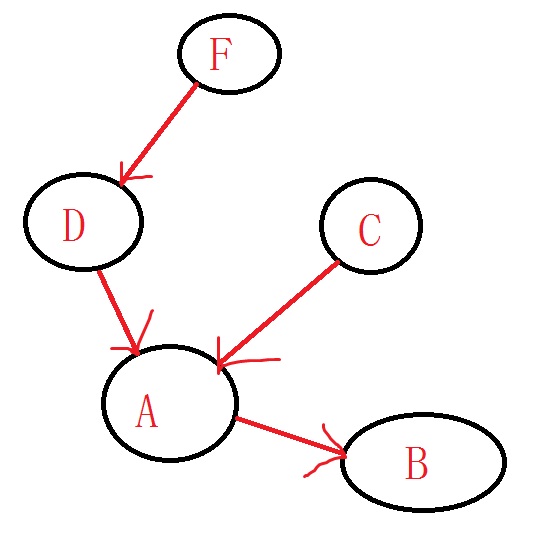
而这个如果像我们前面说的要压缩成一个线性的序列呢。
可以发现。这个答案好像可以有好多种。不止一种。
like F D C A B 或者是 C F D A B 。
好像这些都满足前面的条件。前驱活动一定在后驱活动前面的序列。
这说明一个拓扑排序。不唯一。它有些是没有唯一的答案。几种都可以满足。
3)举一个不能吃的栗子
“选课3”
比如说。我想选修B,但是我必须先选修A。选修A之前我必须选修C。选修C之前。我必须先选修B。
C-》A-》B-》C
靠。这怎么选。选每个都有一个条件。然而这个条件是环形。简直无入口与出口。。
而这个图。就是一个典型的有向环形图。
里面有个环。然而这种情况无法写成线性的拓扑序列。(有本事你写个出来)
所以,前面有讲,拓扑排序必须在有向无环图里面才可以得以实现。
这是个大前提。(重点)。
4)如何实现拓扑排序呢?
有以下几种步骤:
1,选择一个入度为0的点。记录这个点。(如果一个图里,没有一个点的入度为0,则这个图现在是有向环形图)
2,在图中把由这个点为起点的所有边,抹杀掉。(这个点的后驱活动的点的入度--)
3,一直重复前面的动作。把一个一个点抹杀掉。
4,然而当没有入度为0的点。但是图里的点有 没有被抹杀掉的。说明。嗯。这个图里有个环。
这样就完成了我们的拓扑排序。
简单&高效&实用der算法。
the end.