Description
You are to write a program that has to decide whether a given line segment intersects a given rectangle.
An example:
line: start point: (4,9)
end point: (11,2)
rectangle: left-top: (1,5)
right-bottom: (7,1)
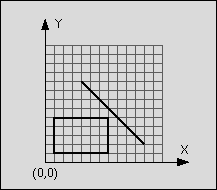
Figure 1: Line segment does not intersect rectangle
The line is said to intersect the rectangle if the line and the rectangle have at least one point in common. The rectangle consists of four straight lines and the area in between. Although all input values are integer numbers, valid intersection points do not have to lay on the integer grid.
An example:
line: start point: (4,9)
end point: (11,2)
rectangle: left-top: (1,5)
right-bottom: (7,1)

Figure 1: Line segment does not intersect rectangle
The line is said to intersect the rectangle if the line and the rectangle have at least one point in common. The rectangle consists of four straight lines and the area in between. Although all input values are integer numbers, valid intersection points do not have to lay on the integer grid.
Input
The input consists of n test cases. The first line of the input file contains the number n. Each following line contains one test case of the format:
xstart ystart xend yend xleft ytop xright ybottom
where (xstart, ystart) is the start and (xend, yend) the end point of the line and (xleft, ytop) the top left and (xright, ybottom) the bottom right corner of the rectangle. The eight numbers are separated by a blank. The terms top left and bottom right do not imply any ordering of coordinates.
xstart ystart xend yend xleft ytop xright ybottom
where (xstart, ystart) is the start and (xend, yend) the end point of the line and (xleft, ytop) the top left and (xright, ybottom) the bottom right corner of the rectangle. The eight numbers are separated by a blank. The terms top left and bottom right do not imply any ordering of coordinates.
Output
For each test case in the input file, the output file should contain a line consisting either of the letter "T" if the line segment intersects the rectangle or the letter "F" if the line segment does not intersect the rectangle.
Sample Input
1 4 9 11 2 1 5 7 1
Sample Output
F
几个需要注意的地方:
①给出的矩形顶点的坐标需要自己重新排下序再使用,看discuss说所谓的top等并不是严格指上方,只是一个相对的参考,所以要重新排下序再用。
②因为题目里面说了矩形的内部也算矩形的一部分,所以线段在矩形内部是认为和矩形相交的。
③在判断线段与矩形四个边是否有交点时,要注意对非规范相交的判定,当线段和边共线且不相交时叉积也为0。
#include<stdio.h>
#include<string.h>
#define zero 1e-8
double xs, ys, xe, ye, xl, yl, xr, yr, x1[5], y1[5], x2[5], y2[5];
double det(double x1, double y1, double x2, double y2)
{
return x1 * y2 - y1 * x2;
}
double fabs(double x)
{
return x < 0 ? -x : x;
}
double min(double x, double y)
{
return x < y ? x : y;
}
double max(double x, double y)
{
return x > y ? x : y;
}
int dcmp(double x)
{
if(fabs(x) < zero)
return 0;
if(x < 0)
return -1;
return 1;
}
int onseg(double x, double y, double x1, double y1, double x2, double y2)
{
if(fabs(x2 - x1) < fabs(y2 - y1))
return dcmp((y - y2) * (y - y1)) <= 0;
else
return dcmp((x - x2) * (x - x1)) <= 0;
}
void solve()
{
int i, j, k;
double t1, t2, t3, t4;
x1[0] = xl, y1[0] = yr, x2[0] = xr, y2[0] = yr;
x1[1] = xl, y1[1] = yr, x2[1] = xl, y2[1] = yl;
x1[2] = xl, y1[2] = yl, x2[2] = xr, y2[2] = yl;
x1[3] = xr, y1[3] = yr, x2[3] = xr, y2[3] = yl;
for(i = 0; i < 4; i ++)
{
t1 = det(x2[i] - x1[i], y2[i] - y1[i], xs - x1[i], ys - y1[i]);
t2 = det(x2[i] - x1[i], y2[i] - y1[i], xe - x1[i], ye - y1[i]);
t3 = det(xe - xs, ye - ys, x1[i] - xs, y1[i] - ys);
t4 = det(xe - xs, ye - ys, x2[i] - xs, y2[i] - ys);
if(dcmp(t1) * dcmp(t2) < 0 && dcmp(t3) * dcmp(t4) < 0)
{
printf("T
");
return ;
}
if((dcmp(t1) == 0 && onseg(xs, ys, x1[i], y1[i], x2[i], y2[i])) || (dcmp(t2) == 0 && onseg(xe, ye, x1[i], y1[i], x2[i], y2[i])) || (dcmp(t3) == 0 && onseg(x1[i], y1[i], xs, ys, xe, ye)) ||(dcmp(t4) == 0 && onseg(x2[i], y2[i], xs, ys, xe, ye)))
{
printf("T
");
return ;
}
}
printf("F
");
}
int main()
{
int i, t;
double x;
scanf("%d", &t);
while(t --)
{
scanf("%lf%lf%lf%lf%lf%lf%lf%lf", &xs, &ys, &xe, &ye, &xl, &yl, &xr, &yr);
if(xl > xr)
x = xl, xl = xr, xr = x;
if(yl < yr)
x = yl, yl = yr, yr = x;
if((xs < xr && xs > xl && ys < yl && ys > yr) || (xe < xr && xe > xl && ye < yl && ye > yr))
printf("T
");
else
solve();
}
return 0;
}