目录:
1.什么是二叉搜索树
2.二叉搜索树的由来与作用
3.二叉搜索树的建立
1.什么是二叉搜索树?
二叉搜索树又称为二叉排序树,它或者是一棵空树,或者是具有一下性质的树:
若它的左子树不空,则左子树上所有的结点的值均不大于它根结点的值;
若它的左子树不空,则左子树上所有的结点的值均不小于它根结点的值;
它的左右子树也是二叉搜索树。
2.二叉搜素树的由来与作用?
假设我们现在有一个数据集,且这个数据集是顺序存储的有序线性表,那么查找可以运用折半、插值、斐波那契二等查找算法来实现,但是因为有序,在插入和删除操作上,就需要耗费大量的时间(需进行元素的移位),能否有一种既可以使得插入和删除效率不错,又可高效查找的数据结构和算法呢?
首先解决一个问题,如何使插入时不移动元素,我们可以想到链表,但是要保证其有序的话,首先得遍历链表寻找合适的位置,那么又如何高效的查找合适的位置呢,能否可以像二分一样,通过一次比较排除一部分元素。那么我们可以用二叉树的形式,以数据集第一个元素为根节点,之后将比根节点小的元素放在左子树中,将比根节点大的元素放在左子树中,在左右子树中同样采取此规则。
例子:将{63,55,90,42,58,70,10,45,67,83}形成二叉树
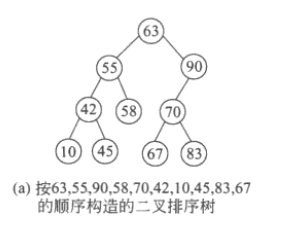
那么在查找x时,若x比根节点小可以排除右子树所有元素,去左子树中查找(类似二分查找),这样查找的效率非常好,而且插入的时间复杂度为O(h),h为树的高度,较O(n)来说效率提高不少。
故二叉搜索树用作一些查找和插入使用比较高的场景。
3.二叉搜索树的建立、查询、最大最小关键字,前驱、后继
先来一个二叉搜索树的结点结构
class BiNode{ public BiNode left; public BiNode right; public BiNode parent; public int data; public BiNode(BiNode left, BiNode right, BiNode parent, int data){ this.left = left; this.right = right; this.parent = parent; this.data = data; } }
在由来之中已经提到,二叉搜索树的建立,是通过一个一个的结点的插入来建立,每个结点有四个域,左右孩子、双亲、数据。
插入算法:将要插入的结点x,与根节点进行比较,若小于则去到左子树进行比较,若大于则去到右子树进行比较,重复以上操作直到找到一个空位置用于放置该新节点
其中root为该树的根节点。
public void insert(BiNode x){ BiNode y = null; BiNode temp = root; while(temp != null){ y = temp; if(x.data < temp.data){ temp = temp.left; }else{ temp = temp.right; } } x.parent = y; //若该树为空树可直接将x放置在根节点上 if(null == y){ root = x; }else if(x.data<y.data){//找到空位置后,进行插入 y.left = x; }else{ y.right = x; } }
建立:可想而知,简单的方法就是遍历数组,将每一个元素插入到二叉搜索树中便完成了建立操作
public BiSortTree(int[] arr,int n){ for(int i=0;i<n;i++){ BiNode node = new BiNode(null, null ,null, arr[i]); insert(node); } }
查询:根据二叉搜索树的性质,将需查找的x与根节点进行比较,若小于则在左子树中继续查询,若大于则在右子树中继续查询,直到查到元素或元素为空
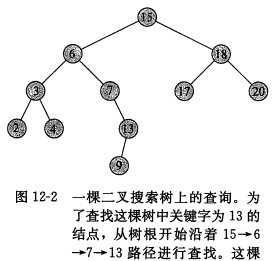
递归查找:
/** * 查找结点,通过递归 * @param x * @return */ public BiNode queryByRec(BiNode root, int x){ if (x == root.data || null == root){ return root; } else if(x < root.data) { return queryByRec(root.left, x); } else { return queryByRec(root.right, x); } }
非递归查找(能不用递归则不用递归,递归会隐式的创建栈,从而浪费内存空间):
/** * 查找结点,非递归,需要传入查找根节点 * @param x * @return */ public BiNode query(BiNode root, int x){ while(null != root && root.data != x){ if(x < root.data){ root = root.left; }else{ root = root.right; } } return root; }
最大最小关键字:这个树中的最大的元素,根据二叉搜索树性质,最大关键字为该树的最右元素,最小关键字为该树的最左元素,故直接将这两个元素搜索出来即可(通过传入根节点可实现查找子树的最大最小关键字元素)
/** * 查找最小关键字元素,即最左结点,需要传入查找根节点 * @return */ public BiNode minNode(BiNode x){ while(x.left!=null){ x=x.left; } return x; } /** * 查找最大关键字元素,即最右结点,需要传入查找根节点 * @return */ public BiNode maxNode(BiNode x){ while(x.right!=null){ x=x.right; } return x; }
查找后继结点:如果我们需要找到以下二叉搜索树的后继,根据需要考虑两种情况
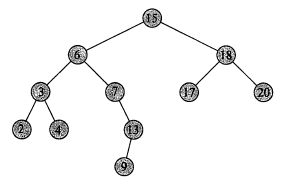
1.如果该节点有右子树,那么它右子树的最小关键字元素便是其后继
2.如果该节点无右子树,由于后继为大于该元素的元素,那么这个结点必在其后继的左子树上,又由于后继为大于该元素的最小元素那么这个后继必然是该节点第一个拥有左孩子的的祖先,综合一下:这个结点的后继为这个结点第一个有左孩子的祖先,且这个左孩子也是这个结点的祖先。
/** * 查找指定数字的后继 * @return */ public BiNode queryFollow(int x){ //首先查找指定结点是否存在 BiNode node = query(root, x); //不存在返回null if(null == node){ return null; } //若该节点有右子树,则其后继为其右子树的最左结点 //若该节点无右子树,则其后继为其第一个拥有左孩子的祖先,且这个左孩子也是该结点的祖先 BiNode p = null; if(node.right!=null){ return minNode(node.right); }else{ p = node.parent; while(null != p && node == p.right){ node = p; p=p.parent; } return p; } }
前驱与后继是相互对应的,不妨自己思考一下,代码如下:
public BiNode queryPre(int x){ BiNode node = query(root, x); BiNode p = null; if(null == node){ return null; } if(node.left!=null){ return maxNode(node.left); }else{ p = node.parent; while(p!=null&&node==p.left){ node=p; p=p.parent; } return p; } }