gu集合

离散型随机变量的一切可能的取值  与对应的概率  乘积之和称为该离散型随机变量的数学期望，本题期望是概率乘得分之和

数列是递增的，可以枚举第二小的数，假设选第i个数为第2小的数，则第1小的数有i-1种选择，其余k-2个数，在第i+1~n个数中选择，得出选第i个数为第2小的数的概率为：

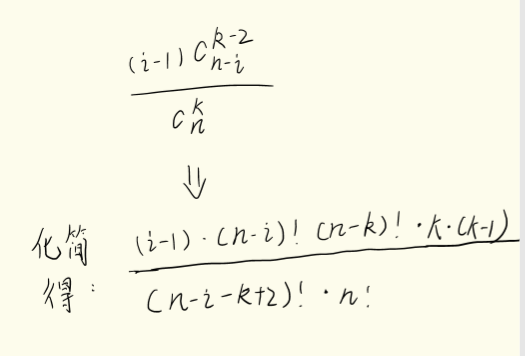
为求概率，要先预处理阶乘。我们知道（p*q）%m=（p%m）*（q%m）%m，但这个算式还有除法，需要用到逆元，我用的是阶乘的逆元 ，所以再预处理一下阶乘的逆元。

这样概率就求出来啦。

再求得分 c^g(T)!

很显然g(T)为我们枚举的第2小的数的值

我们知道（p*q）%m=（p%m）*（q%m）%m，但仔细观察一下这个规则没法求c^g(T)!，两者没有直接的关系，这地方很容易出错。

可以用费马小定理来求c^g(T)!  费马小定理：如果p是一个质数，而整数a不是p的倍数，则有a^（p-1）≡1（mod p）。

根据小定理我们发现，如果p是一个质数，a的整数次幂%p是周期性的，(a^0)%p=1,[a^(p-1)]%p=1,所以指数从0~p-2是一个周期，而998244353确实是质数，我们就可以把指数%（p-1），也就是把阶乘%（p-1），再把整个幂%p来求c^g(T)!，这里同样需要预处理阶乘。

这样期望就求出来啦。

因为好多数据需要预处理，超了一次内存，修改思路比较笨拙，就不多讲了。

#include<bits/stdc++.h>
#define ll long long
#define scl(x) scanf("%lld",&x)
#define sc(x) scanf("%d",&x)
using namespace std;
int p=998244353;
 
int inv[510000];
int s[510000];
int fc[10000010];
int fc2[10000010];
int kk=500000;
int tt=10000001;
 
ll pw(ll a,ll n,ll m)//快速幂 
{
 if(n==0)return 1;
 ll x=pw(a,n/2,m);
 ll ans=(ll)x*x%m;
 if(n%2==1)ans=ans*a%m;
 return (ll)ans;
}
 
int main()
{
  fc[0]=1;
  fc[1]=1;
  ll mn; 
  for(int i=2;i<=tt;i++)//阶乘%p 
  {
   mn=(ll)fc[i-1]*i;
   mn%=p;
   fc[i]=mn;
  }
   
  fc2[0]=1;
  fc2[1]=1;
  for(int i=2;i<=tt;i++)//阶乘%（p-1） 
  {
   mn=(ll)fc2[i-1]*i;
   mn%=(p-1);
   fc2[i]=mn;
  }
   
  inv[kk]=pw(fc[kk],p-2,p);
  for(int i=kk-1;i>=0;i--)//阶乘逆元 
  {
   mn=(ll)inv[i+1]*(i+1);
   mn%=p;
   inv[i]=mn;
  }
   

  int n,k;
  ll c;
  sc(n);
  sc(k);
  scl(c);
   
  for(int i=1;i<=n;i++)
  scl(s[i]);
   
  ll anss=0;
  for(int i=2;k-2<=n-i;i++)//计算期望 
  {
   ll temp=i-1;
   temp*=k;
   temp*=(k-1);
   temp%=p;
   temp*=(ll)fc[n-i];
   temp%=p;
   temp*=(ll)fc[n-k];
   temp%=p;
   temp*=(ll)inv[n];
   temp%=p;
   temp*=(ll)inv[n-i-k+2];
   temp%=p;
   ll g=s[i];
   ll temp2=pw(c,fc2[g],p);  
   anss+=temp*temp2;
   anss%=p;
  }
  printf("%lld
",anss);
}